通关算法题之 ⌈二叉树⌋ 上
二叉树深度
104、求二叉树最大深度
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数,叶子节点是指没有子节点的节点。
示例:
给定二叉树[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3。
解法一:递归遍历二叉树,回溯算法思路
遍历一遍二叉树,用一个外部变量记录每个节点所在的深度,取最大值就可以得到最大深度。
class Solution {
public:
int depth = 0;
int res = 0;
int maxDepth(TreeNode* root) {
traverse(root);
return res;
}
//遍历二叉树
void traverse(TreeNode* root){
if(root == nullptr){
return;
}
//前序遍历位置
depth++;
//遍历过程中记录最大深度
res = max(depth, res);
traverse(root->left);
traverse(root->right);
//后序遍历位置
depth--;
}
};
解法二:分解成子树问题,动态规划思路
class Solution {
public:
// 定义:输入一个节点,返回以该节点为根的二叉树的最大深度
int maxDepth(TreeNode* root) {
if(root == nullptr){
return 0;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
// 根据左右子树的最大深度推出原二叉树的最大深度
return max(leftDepth, rightDepth) + 1;
}
};
解法三:层序遍历
class Solution {
public:
int maxDepth(TreeNode* root) {
int depth = 0;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return depth;
}
};
求二叉树的最大深度可以延伸到求二叉树的直径:
543、二叉树直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
每一条二叉树的「直径」长度,就是一个节点的左右子树的最大深度之和。把计算「直径」的逻辑放在后序位置,准确说应该是放在 maxDepth 的后序位置,因为 maxDepth 的后序位置是知道左右子树的最大深度的。
class Solution {
public:
int maxDiameter = 0;
int diameterOfBinaryTree(TreeNode* root) {
maxDepth(root);
return maxDiameter;
}
//定义:输入一个节点,返回以该节点为根节点的二叉树的深度
int maxDepth(TreeNode* root){
if(root == nullptr){
return 0;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
// 后序位置,顺便计算最大直径
maxDiameter = max(leftDepth + rightDepth, maxDiameter);
return max(leftDepth, rightDepth) + 1;
}
};
111、二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
示例:给定二叉树[3,9,20,null,null,15,7]:
3
/ \
9 20
/ \
15 7
返回它的最小深度2。
解法一:分解成子树问题,动态规划思想
class Solution {
public:
//定义:输入一个节点,返回以该节点为根节点的二叉树的最小深度
int minDepth(TreeNode* root) {
if(!root) {
return 0;
}
int leftDepth = minDepth(root->left);
int rightDepth = minDepth(root->right);
return min(leftDepth, rightDepth) + 1;
}
};
❓上面的算法对吗?为什么?
❎错误!
✅正确的解法一:分解成子树问题,动态规划思想
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root){
return 0;
}
int leftDepth = minDepth(root->left);
int rightDepth = minDepth(root->right);
if(!root->left){
return rightDepth + 1;
}
if(!root->right){
return leftDepth + 1;
}
return min(leftDepth, rightDepth) + 1;
}
};
解法二:层序遍历
class Solution {
public:
int minDepth(TreeNode* root) {
int depth = 0;
queue<TreeNode*> que;
if(root) que.push(root);
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
if(!node->left && !node->right) return depth;
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return depth;
}
};
110、平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 :
输入:root = [3,9,20,null,null,15,7]
输出:true
本题依然是二叉树深度相关的题目,依然是把计算「高度差」的逻辑放在后序位置,准确说应该是放在 maxDepth 的后序位置,因为 maxDepth 的后序位置是知道左右子树的最大深度的。
只计算一次最大深度,计算的过程中在后序遍历位置顺便判断二叉树是否平衡:对于每个节点,先算出来左右子树的最大高度,然后在后序遍历的位置根据左右子树的最大高度判断平衡性。
class Solution {
public:
// 记录二叉树是否平衡
bool balance = true;
bool isBalanced(TreeNode* root) {
maxDepth(root);
return balance;
}
// 定义:输入一个节点,返回以该节点为根的二叉树的最大深度
int maxDepth(TreeNode* root){
if(!root) return 0;
int leftDepth= maxDepth(root->left);
int rightDepth = maxDepth(root->right);
if(abs(leftDepth - rightDepth) > 1) balance = false;
return max(leftDepth, rightDepth) + 1;
}
};
翻转二叉树
226、翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
解法一:递归遍历,回溯算法的思想
遍历二叉树的每个节点,每个节点的左、右子树交换位置。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
traverse(root);
return root;
}
// 二叉树遍历函数
void traverse(TreeNode* root){
if(!root){
return;
}
// 每一个节点需要做的事就是交换它的左右子节点
TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
// 遍历框架,去遍历左右子树的节点
traverse(root->left);
traverse(root->right);
}
};
解法二:分解为子树的问题,动态规划思想
用 invertTree(x.left) 先把 x 的左子树翻转,再用 invertTree(x.right) 把 x 的右子树翻转,最后把 x 的左右子树交换,这恰好完成了以 x 为根的整棵二叉树的翻转,即完成了 invertTree(x) 的定义。
class Solution {
public:
//定义:输入一个节点,将以该节点为根节点的二叉树进行翻转,返回其根节点
TreeNode* invertTree(TreeNode* root) {
if(!root) {
return root;
}
// 利用函数定义,先翻转左右子树
TreeNode* left = invertTree(root->left);
TreeNode* right = invertTree(root->right);
// 然后交换左右子节点
root->left = right;
root->right = left;
return root;
}
};
解法三:层序遍历
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
stack<TreeNode*> st;
st.push(root);
while(!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
swap(node->left, node->right);
if(node->right) st.push(node->right); // 右
if(node->left) st.push(node->left); // 左
}
return root;
}
};
路径总和
112、路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
示例:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
解法一:递归遍历,回溯算法思想
前部遍历位置(进入节点)sum += root->val,顺便判断是否到达叶子节点且和为targetSum;后序遍历位置(离开节点)sum -= root->val。
class Solution {
public:
bool res = false;
int sum = 0;
bool hasPathSum(TreeNode* root, int targetSum) {
traverse(root, targetSum);
return res;
}
void traverse(TreeNode* root, int targetSum){
if(!root) return;
//前序遍历位置
sum += root->val;
// 到达叶子节点且和为targetSum
if(!root->left && !root->right && sum == targetSum) res = true;
traverse(root->left, targetSum);
traverse(root->right, targetSum);
//后序遍历位置
sum -= root->val;
}
};
解法二:分解成子树问题,动态规划思想
遍历到一个节点,继续遍历左孩子和右孩子,且targetSum减去节点的数值。
class Solution {
public:
// 定义:输入一个根节点,返回该根节点到叶子节点是否存在一条和为 targetSum 的路径
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
if(!root->left && !root->right && root->val == targetSum) return true;
// 左子树或者右子树有一个满足即可
return hasPathSum(root->left, targetSum - root->val) ||
hasPathSum(root->right, targetSum - root->val);
}
};
113、路径总和ii
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
示例:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
相对于⌈112、路径总和⌋来说,前序和后序位置不仅要维护sum,还要维护路径path。
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
int sum = 0;
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
traverse(root, targetSum);
return res;
}
void traverse(TreeNode* root, int targetSum){
if(!root) return;
//前序遍历位置
sum += root->val;
path.push_back(root->val);
if(!root->left && !root->right && sum == targetSum) res.push_back(path);
traverse(root->left, targetSum);
traverse(root->right, targetSum);
//后序遍历位置
sum -= root->val;
path.pop_back();
}
};
437、路径总和iii
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例:
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示
这题及要求你准确理解二叉树的前序后序遍历,还要熟悉前缀和技巧,把前缀和技巧用到二叉树上。
这道题涉及到数组的技巧,暂定先不做。
二叉树是否对称/相等
101、对称二叉树和100、相同的树结合起来看,两道题方法和代码上非常相似。
100、相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例:
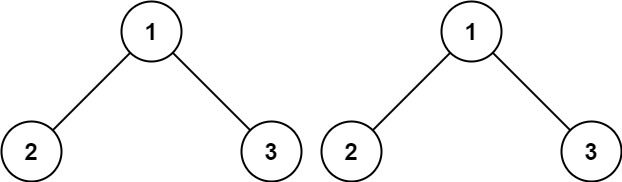
输入:p = [1,2,3], q = [1,2,3]
输出:true
解法一:分解成子树问题
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p || !q) return p == q;
if(p->val != q->val) return false;
bool left = isSameTree(p->left, q->left); //比较左子树
bool right = isSameTree(p->right, q->right);//比较右子树
return left && right;
}
};
代码简化为:
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 判断一对节点是否相同
if(!p || !q) return p == q;
if(p->val != q->val) return false;
// 判断其他节点是否相同
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
解法二:迭代法
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
queue<TreeNode*> que;
que.push(p);
que.push(q);
//注意不能加上写成如下代码,否则会报错
//if(p) que.push(p);
//if(q) que.push(q);
while (!que.empty()) { // 接下来就要判断这两颗树是否相等
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是相等的
continue;
}
// 左右一个节点不为空,或者都不为空但数值不相同,返回false
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left);
que.push(rightNode->left);
que.push(leftNode->right);
que.push(rightNode->right);
}
return true;
}
};
注意:
que.push(p);
que.push(q);
不能写为:
if(p) que.push(p);
if(q) que.push(q);
否则会报错:
执行出错信息:
Line 15: Char 74: runtime error: member access within misaligned address 0xbebebebebebebebe for type 'TreeNode', which requires 8 byte alignment (solution.cpp)
0xbebebebebebebebe: note: pointer points here
<memory cannot be printed>
SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:24:74
最后执行的输入:
[]
[0]
加上if判断后,若输入当中有为空的,则无法加入到队列当中,影响后序的代码逻辑运行。
101、对称二叉树
给定一个二叉树,检查它是否是镜像对称的。

解法一:分解成子树问题
对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两颗树(这两颗树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中,只有内侧和外侧节点分别对应相等,这两棵树才是对称的。
返回条件:
- 左节点为空,右节点不为空,不对称,return false;
- 左不为空,右为空,不对称 return false;
- 左右都为空,对称,返回true;
- 左右都不为空,比较节点数值,不相同就return false;
- 左右节点相等的话,再递归判断子节点;
代码如下:
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return compare(root->left, root->right);
}
//定义:输入左、右节点,返回分别以这两节点为根节点的二叉树是否对称
bool compare(TreeNode* left, TreeNode* right){
// 注意这里终止条件的代码
if(!left || !right) return left == right;
if(left->val != right->val) return false;
bool outside = compare(left->left, right->right); //外侧节点比较
bool inside = compare(left->right, right->left); //内侧节点比较
return outside && inside; //左右子节点需要对称相同
}
};
代码简化为:
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return compare(root->left, root->right);
}
//定义:输入左、右节点,返回分别以这两节点为根节点的二叉树是否对称
bool compare(TreeNode* left, TreeNode* right){
// 该对节点是否对称
if(!left || !right) return left == right;
if(left->val != right->val) return false;
// 其他节点是否对称
return compare(left->left, right->right) && compare(left->right, right->left);
}
};
解法二:迭代法,不是层序遍历,这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转。
把左右两个子树要比较的元素顺序放进一个容器,然后成对的取出来进行比较,那么其实使用栈也是可以的。
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
queue que;
que.push(root->left); // 将左子树头结点加入队列
que.push(root->right); // 将右子树头结点加入队列
while (!que.empty()) { // 接下来就要判断这两个树是否相互翻转
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的
continue;
}
// 左右一个节点不为空,或者都不为空但数值不相同,返回false
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left); // 加入左节点左孩子
que.push(rightNode->right); // 加入右节点右孩子
que.push(leftNode->right); // 加入左节点右孩子
que.push(rightNode->left); // 加入右节点左孩子
}
return true;
}
};
572、另一个树的子树
给你两棵二叉树 root 和 subRoot ,检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点,tree 也可以看做它自身的一棵子树。
示例:
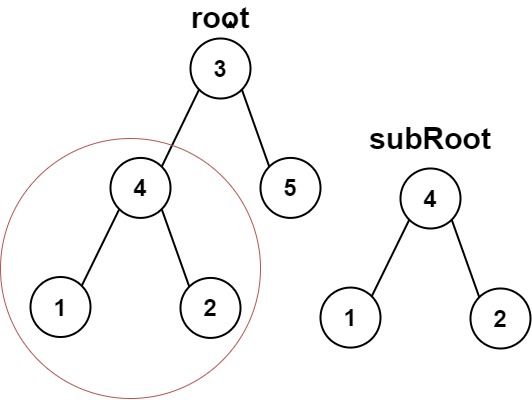
输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
遍历以 root 为根的这棵二叉树的所有节点,用 ⌈100、相同的树⌋ 中的 isSameTree 函数判断以该节点为根的子树是否和以 subRoot 为根的那棵树相同。
class Solution {
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if(!root) return root == subRoot;
// 判断以 root 为根的二叉树是否和 subRoot 相同
if(isSameTree(root, subRoot)) return true;
// 去左右子树中判断是否有和 subRoot 相同的子树
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
// 定义:输入两个节点,判断以两个节点为根节点的二叉树是否一样,返回结果
bool isSameTree(TreeNode* p, TreeNode* q) {
// 判断一对节点是否相同
if(!p || !q) return p == q;
if(p->val != q->val) return false;
// 判断其他节点是否相同
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
左叶子/左下角问题
404、左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例:
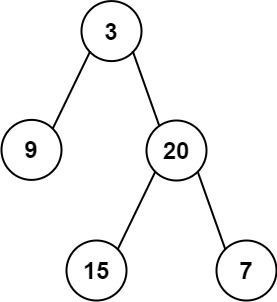
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
首先要注意是判断左叶子,不是二叉树左侧节点,所以不要上来想着层序遍历。
本题遍历二叉树即可,问题是如何判断节点是左叶子呢?
如果左节点不为空,且左节点没有左右孩子,那么这个节点的左节点就是左叶子,必须要通过节点的父节点来判断其左孩子是不是左叶子:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
左叶子节点处理逻辑
}
class Solution {
public:
int sum = 0;
int sumOfLeftLeaves(TreeNode* root) {
traverse(root);
return sum;
}
void traverse(TreeNode* root){
if(!root) return;
// 找到左侧的叶子节点,记录累加值
if(root->left && !root->left->left && !root->left->right){
sum += root->left->val;
}
traverse(root->left);
traverse(root->right);
}
};
513、找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例:
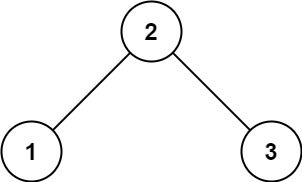
输入: root = [2,1,3]
输出: 1
解法一:递归遍历二叉树
二叉树递归框架代码是先递归左子树,后递归右子树,所以到最大深度时第一次遇到的节点就是左下角的节点。
class Solution {
public:
int depth; // 记录 traverse 递归遍历到的深度
int maxDepth; // 记录二叉树的最大深度
TreeNode* res;
int findBottomLeftValue(TreeNode* root) {
traverse(root);
return res->val;
}
void traverse(TreeNode* root){
if(!root) return;
depth++;
// 到最大深度时第一次遇到的节点就是左下角的节点
if(depth > maxDepth){
maxDepth = depth;
res = root;
}
traverse(root->left);
traverse(root->right);
depth--;
}
};
解法二:层序遍历,很好理解
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0; //后续循环会不断刷新result的值
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) result = node->val; // 记录最后一行第一个元素
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
};
找树左下角的值会做了,找树右下角的值自然也会做了,也就是把遍历的顺序改变一下:先遍历右子树,再遍历左子树。
完全二叉树
BM35 判断是不是完全二叉树
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
样例图1:叶子节点出现在最后一层
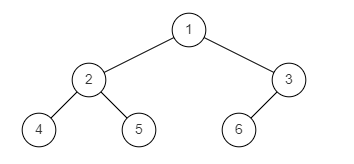
样例图2:叶子节点出现在最后一次和倒数第二层
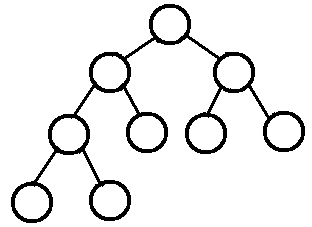
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
本道题的解题关键就是要紧紧抓住完全二叉树的定义,使用层序遍历。如果遇到某个节点为空,进行标记,代表访问到完全二叉树的最下层,若是后续还有访问,则不符合完全二叉树的定义。
注意:
que.push(node->left);
que.push(node->right);
不能写成:
if(node->left) push(node->left);
if(node->right) que.push(node->right);
否则, 完全二叉树最后一层的空节点是访问不到的。
class Solution {
public:
bool isCompleteTree(TreeNode* root) {
//空树一定是完全二叉树
if(root == NULL) return true;
queue<TreeNode*> que;
if(root) que.push(root);
//定义一个首次出现的标记位
bool flag = false;
while(!que.empty()){
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
//标记第一次遇到空节点
if (!node)
flag = true;
else{
//后续访问已经遇到空节点了,说明经过了叶子
if (flag) return false;
que.push(node->left);
que.push(node->right);
}
}
}
return true;
}
};
222、完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
示例:
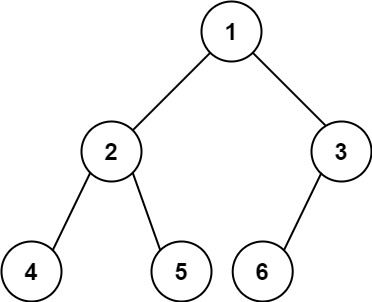
输入:root = [1,2,3,4,5,6]
输出:6
首先要搞清楚什么是 ⌈完全二叉树⌋ 和 ⌈满二叉树⌋ :
完全二叉树如下图,每一层都是紧凑靠左排列的,除了最底层节点可能没填满外,其余每层节点数都达到最大值:
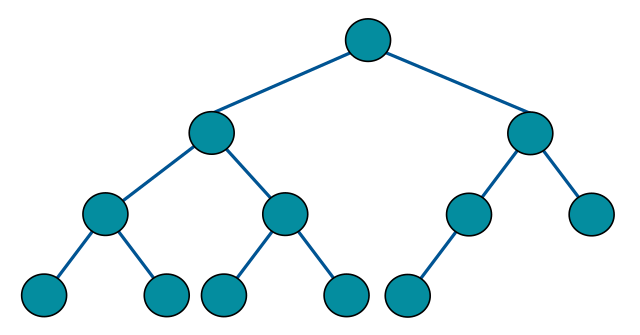
满二叉树如下图,是一种特殊的完全二叉树,每层都是是满的,像一个稳定的三角形:
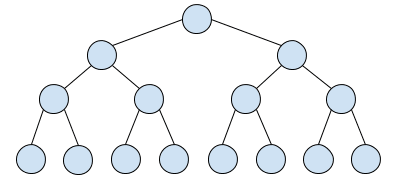
如果是一个普通二叉树,显然只要向下面这样遍历一边即可,时间复杂度 O(N):
int countNodes(TreeNode* root) {
if (root == null) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
那如果是一棵满二叉树,节点总数就和树的高度呈指数关系:
int countNodes(TreeNode* root) {
int h = 0;
// 计算树的高度
while (root != null) {
root = root->left;
h++;
}
// 节点总数就是 2^h - 1
return (2 << h) - 1;
}
完全二叉树比普通二叉树特殊,但又没有满二叉树那么特殊,计算它的节点总数,可以说是普通二叉树和完全二叉树的结合版。
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
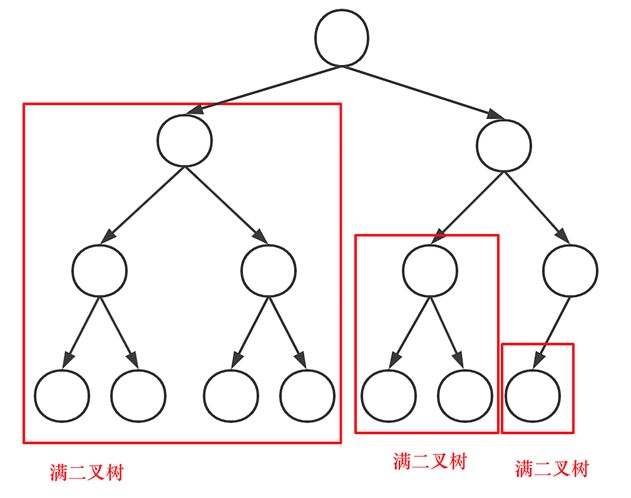
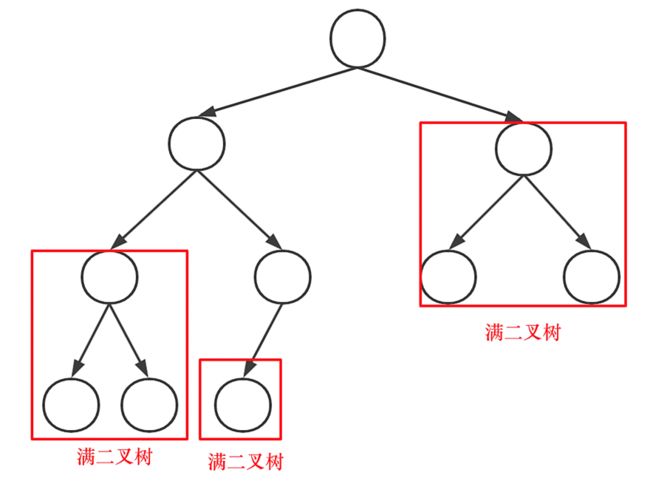
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
class Solution {
public:
int countNodes(TreeNode* root) {
if (!root) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
// 这里初始为0是有目的的,为了下面求指数方便
int leftHeight = 0;
int rightHeight = 0;
// 记录左、右子树的高度
while (left) {
left = left->left;
leftHeight++;
}
while (right) {
right = right->right;
rightHeight++;
}
// 如果左右子树的高度相同,则是一棵满二叉树
if (leftHeight == rightHeight) {
return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2,所以leftHeight初始为0
}
// 如果左右高度不同,则按照普通二叉树的逻辑计算
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
这个算法的时间复杂度是 O(logN*logN),但直觉感觉好像最坏情况下是 O(N*logN) ,因为之前的 while 需要 logN 的时间,最后要 O(N) 的时间向左右子树递归:
return 1 + countNodes(root.left) + countNodes(root.right);
关键点在于,这两个递归只有一个会真的递归下去,另一个一定会触发 leftHeight == rightHeight 而立即返回,不会递归下去。
所以,算法的递归深度就是树的高度 O(logN),每次递归所花费的时间就是 while 循环,需要 O(logN),所以总体的时间复杂度是 O(logN*logN)。
二叉树展开为链表
114、二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 前序遍历 顺序相同。
示例 :
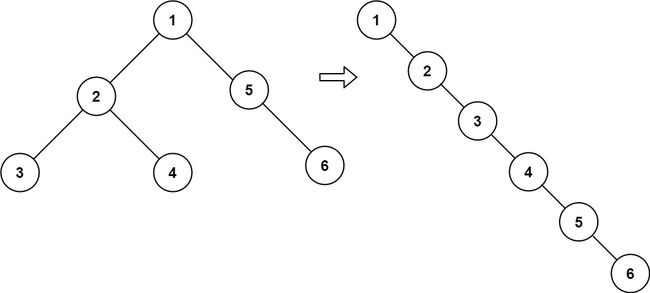
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
解法一:递归遍历
对整棵树进行前序遍历,一边遍历一边构造出一条「链表」。
class Solution {
public:
// 虚拟头节点,res->right 就是结果
TreeNode* res = new TreeNode(-1);
// 用来构建链表的指针
TreeNode* p = res;
TreeNode* flatten(TreeNode* root) {
traverse(root);
return res->right;
}
void traverse(TreeNode* root){
if(!root) return;
p = new TreeNode(root->val);
p = p->right;
traverse(root->left);
traverse(root->right);
}
};
但是注意 flatten 函数的签名,返回类型为 void,也就是说题目希望我们在原地把二叉树拉平成链表。
这样一来,没办法通过简单的二叉树遍历来解决这道题了。
解法二:分解成子树的问题
对于一个节点 x,可以执行以下流程:
1、先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。
2、将 x 的右子树接到左子树下方,然后将整个左子树作为右子树。
这样,以 x 为根的整棵二叉树就被拉平了,恰好完成了 flatten(x) 的定义。
class Solution {
public:
//定义:输入一个节点,将以该节点为根节点的二叉树展开成单链表
void flatten(TreeNode* root) {
if(!root) return;
// 利用定义,把左右子树拉平
flatten(root->left);
flatten(root->right);
// 1、左右子树已经被拉平成一条链表
TreeNode* left = root->left;
TreeNode* right = root->right;
// 2、将左子树作为右子树
root->left = nullptr;
root->right = left;
// 3、将原先的右子树接到当前右子树的末端
TreeNode* p = root;
// 注意这里的条件是 p->right,而不是 p ,即有右孩子则移动指针
while(p->right){
p = p->right;
}
p->right = right;
}
};