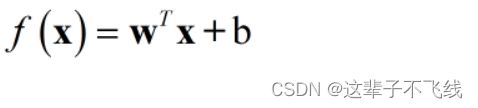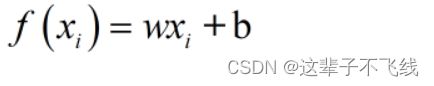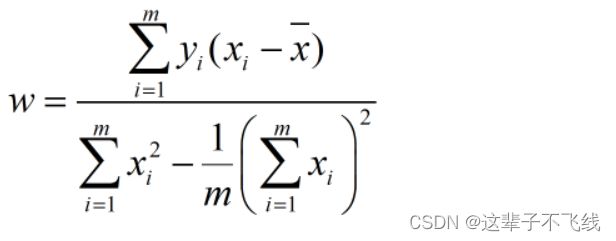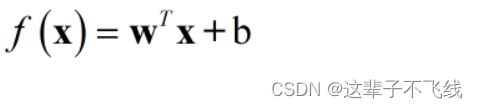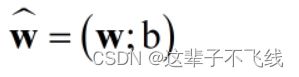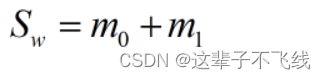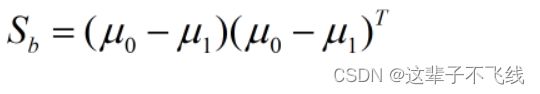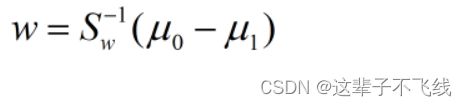吃瓜第二弹——线性模型
最近几天时间,我主要学习了西瓜书上第三章线性模型的相关内容。
0 线性模型综述
线性模型的基本形式与我们初中时候的一次函数形式相似,即函数值等于权重向量乘以自变量矩阵加上偏置项。
当线性模型的权重矩阵和偏置项学得之后,整个模型就会得以确定。
线性模型形式简单、易于建模,且具有很好的可解释性,许多非线性模型都需要基于线性模型得到。
利用线性模型,我们主要解决回归和分类的一些问题。
1 回归
1 线性回归
一元线性回归,试图学得
使得
之所以要约等于,是为了缓解过拟合现象的发生。
那么我们如何确定权重和偏置呢?这时我们想到了均方误差,只要让预测值和实际值的均方误差最小即可。
鉴于这个均方误差的函数是一个凸函数并且不存在最大值,所以我们让均方误差函数分别对w和b求偏导并令两式为0,就可以得到二者的最优解。
二者的最优解如下
本章内容的思路,基本都和一元线性回归的求解思路相同。先写出线性表达式的形式,再想办法确定权重和偏置的参数值,从而确定模型。
多元线性回归,与一元线性回归类数类似,则是
使得估计值约等于真实值。
确定权重向量和偏置时,类似一元线性回归的做法,对均方误差求导并置零可得出结果,这里仅对结果做出一些讨论。
将w和b吸收入向量形式使
令矩阵X为每个自变量一个m×2的矩阵,其中第一列为自变量向量,第二列为1。
当X的转置和X相乘得到满秩矩阵或正定矩阵时,可以得到线性回归模型为
若不满足上述条件,w将不存在唯一解,将由学习算法的归纳偏好决定。
2 对数线性回归(广义线性模型)
对数线性回归定义如下
其实还可以把这里的对数函数换成任何单调可微函数,这样的模型称为广义线性模型。
2 分类
3 对数几率回归
受到广义线性模型启发,如果我们可以找到一个单调可微函数将回归模型预测值和预测真实标记联系起来就可以了。
这样的函数,最理想的莫过于单位阶跃函数了,单位阶跃函数可以直接将所有自变量分为0和1两类。但是阶跃函数不可微,所以我们要想办法用显示存在的函数逼近单位阶跃函数。
我们采用对数几率函数来代替单位阶跃函数,其表达式如下
将上式的自然对数的指数部分的相反数令为z,可以得到z和y的函数图像如下
将上式进行反解可以得到
这是一种“Sigmoid函数”。我们认为g(z)值大于0.5时为一类,小于0.5时为另外一类。
之所以称其为对数几率函数,假设我们有一个二分类问题,将所有的样本分为正例和反例两种。我们设y为正例的可能性,则1-y可以用来表示反例的可能性。我们定义正例的可能性与反例的可能性的比值为几率,给几率取对数就是对数几率,即z就是对数几率。
同样的,我们需要确定权重和偏置从而确定模型。由于之前使用的均方误差方法对该模型不再适用(因为该模型的均方误差函数非凸),我们采用极大似然估计的方法进行求解。
简单来说,我们想要让预测为正例的可能性乘实际为正例的可能性加上预测为反例的可能性乘实际为反例的可能性越大越好,通过一系列的变换最终得到一个目标函数,我们使用梯度下降法等方法得到最优解。
4 线性判别分析(Linear Discriminant Alalysis,LDA)
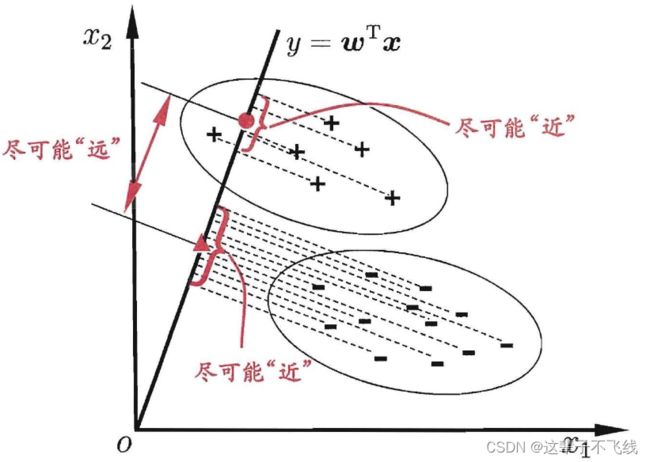
线性判别分析,是一种常用的二分类方法,其思想如下:
将所有的训练数据投影到一条直线上,尽可能使同类样例的投影点接近,异类投影点远离;对新样本进行分类时,观察其投影位置确定类别。
我们希望同类样例的投影点协方差尽可能小,异类样例投影点的类中心距离尽可能大。设X、μ、m分别表示两类的实例、均值向量和协方差向量,直线的方向向量为w,经过投影,我们可以得到如下最大化的目标
定义类内散度矩阵(表征同一类的离散程度,希望其尽可能小)有
类间散度矩阵(表征不同类之间的离散程度,希望其尽可能大)有
所以优化目标变成了上述两个矩阵的广义瑞利商。通过拉格朗日乘子的方法,得到了
此时的w就是最优解。
5 多分类学习
我们通常将多分类问题会分解为多个二分类问题进行,即“拆解法”。最基本的拆解策略有“一对一”“一对其余”“多对多”。
所谓“一对一”,就是将多分类学习分解成为N(N-1)/2个二分类问题(选择器),最终通过投票的方式得到最终结果,即两两pk,统计每一个胜者出现的次数,次数最多的就是最终结果。
所谓“一对其余”,就是将多分类学习中的其中一类拿出来,剩下的为另一类,即将多分类学习分解成为N个二分类问题(选择器),同样找出预测结果中出现次数最多的那个为最终结果。
“多对多”,这里以"纠错输出码”(ECOC)为例。将N个类进行M次划分(选择器),在每个选择器中进行分类,取最终距离最小(海明距离、欧几里得距离等均可)的为最终结果。
例如有甲、乙、丙、丁四个种类,现在有一个样本C不知道属于哪一个分类。这里有五个分类器(M=5),第一个分类器中甲、丙、丁为一类(1A),第二个分类器中只有乙(1B),样本C在这一次分类中分入了1A;第二个分类器中甲、丙为一类(2A),其余为另一类(2B),C分入了2B;第三个分类器甲乙为一类(3A),其余为一类(3B),C分入了3B;第四个分类器甲乙丁为一类(4A),C分入了4B;第五个分类器甲、丙为一类(5A),其余为另一类(5B),C分入了5B;通过计算海明距离和欧几里得距离,该样本均和丙类距离最近,所以属于丙类。
这种方法具有一定的容忍和修正能力,出现错误编码时仍可能产生正确的分类结果。ECOC编码越长纠错能力越强,但是同时意味着所需的分类器越多。
6 类别不平衡问题
如果训练样例中两种类别的数目差异很大,我们需要进行再缩放。
其中m-为反例数目,m+为正例数目。
目前碰到类别不平衡的问题有三种做法:对于样例数目太多的一类进行“欠采样”,对于样例过少的一类进行“过采样”,还有一种就是“再缩放”的思想。
欠采样的时候很可能有一些重要信息被舍弃,过采样又有可能出现严重的过拟合现象。
以上就是线性模型这一章内容的笔记和整理。