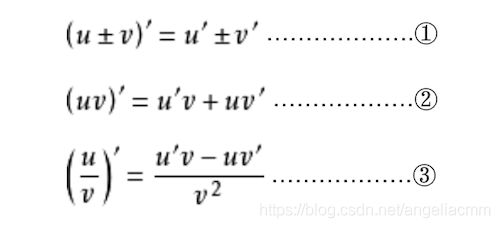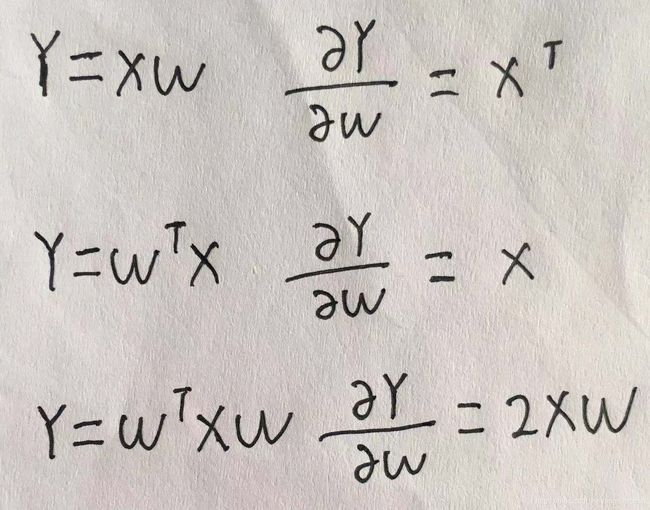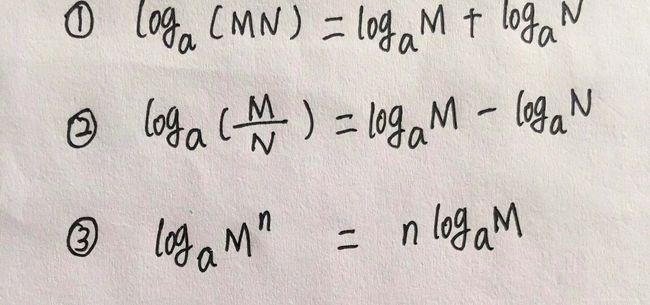学习TensorFlow数学基础知识准备阶段1

最近准备入手TensorFlow深度学习，奈何很多数学基础知识全部都已经回交给各位老师了。因此从刚开始的无从下手，到现在还可以推导一些公式。把我在这个过程中回顾整理的内容，自我留档，同时也分享给大家，希望可以对有兴趣学习TensorFlow但又无从下手的朋友有一些提示作用。

这篇博客只是整理了推导 线性回归 和 逻辑回归 所使用到的数学内容。后期整理出其他部分内容的再给大家分享。

以下数学内容都属于基础知识，涵盖了高中和大学学习的部分内容，主要体现在导数（高中数学），高等数学（上册），线性代数，概率论等。

1.导数

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。
对于可导的函数f(x)，x↦f’(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。反之，已知导函数也可以倒过来求原来的函数，即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

1.1定义

设函数y=f（x）在点x0的某个邻域内有定义，当自变量x在x0处有增量Δx，（x0+Δx）也在该邻域内时，相应地函数取得增量Δy=f（x0+Δx）-f（x0）；如果Δy与Δx之比当Δx→0时极限存在，则称函数y=f（x）在点x0处可导，并称这个极限为函数y=f（x）在点x0处的导数记作：

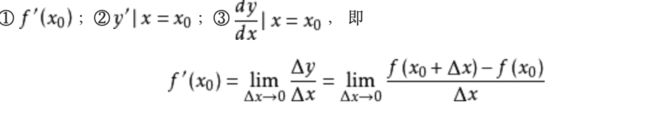
需要指出的是：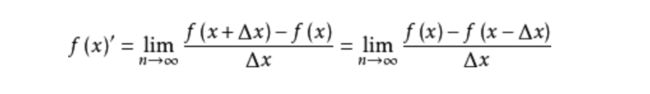
两者在数学上是等价的。

1.1.1导函数

如果函数y=f（x）在开区间内每一点都可导，就称函数f（x）在区间内可导。这时函数y=f（x）对于区间内的每一个确定的x值，都对应着一个确定的导数值，这就构成一个新的函数，称这个函数为原来函数y=f（x）的导函数，记作y’、f’（x）、dy/dx或df（x）/dx，简称导数。
导数是微积分的一个重要的支柱。牛顿及莱布尼茨对此做出了贡献。

1.1.2几何意义

函数y=f（x）在x0点的导数f’（x0）的几何意义：表示函数曲线在点P0（x0,f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

1.2求导公式

以下是6组是我们最经常用到的求导公式，其中在线性回归和逻辑回归中需要使用的为前4组。

1.2.1 导数的四则运算

1.2.2 复合函数求导

复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数（称为链式法则）。
具体求导规则，大家可以通过下方案例自行理解：

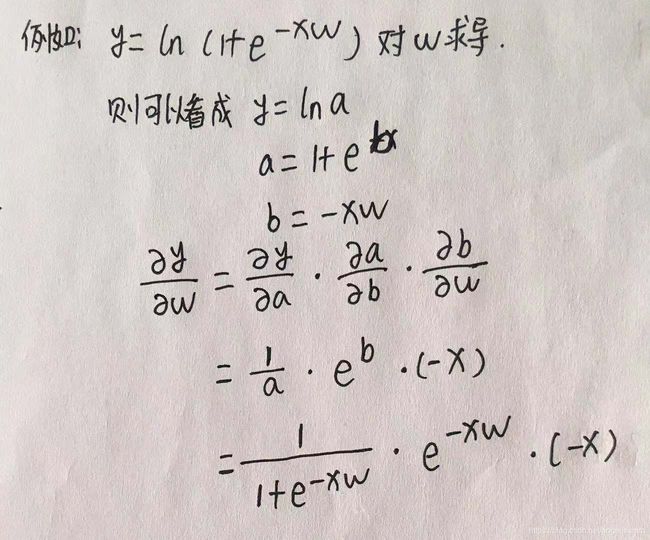
1.3导数与函数的性质编辑

1.3.1 单调性

（1）若导数大于零，则单调递增；若导数小于零，则单调递减；导数等于零为函数驻点，不一定为极值点。需代入驻点左右两边的数值求导数正负判断单调性。
（2）若已知函数为递增函数，则导数大于等于零；若已知函数为递减函数，则导数小于等于零。
根据微积分基本定理，对于可导的函数，有：
如果函数的导函数在某一区间内恒大于零（或恒小于零），那么函数在这一区间内单调递增（或单调递减），这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点，在这类点上函数可能会取得极大值或极小值（即极值可疑点）。进一步判断则需要知道导函数在附近的符号。对于满足的一点，如果存在使得在之前区间上都大于等于零，而在之后区间上都小于等于零，那么是一个极大值点，反之则为极小值点。

1.3.2 凹凸性

可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增，那么这个区间上函数是向下凹的，反之则是向上凸的。如果二阶导函数存在，也可以用它的正负性判断，如果在某个区间上恒大于零，则这个区间上函数是向下凹的，反之这个区间上函数是向上凸的。曲线的凹凸分界点称为曲线的拐点。

关于导数这部分内容如果感觉观看文字效果不好，推荐大家可以去爱奇艺上看看这个视频，http://www.iqiyi.com/u/1470520766/a 个人感觉完全可以满足我们快速回顾导数内容的需求。

2. 偏导数

在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。偏导数在向量分析和微分几何中是很有用的。

2.1 引入

在一元函数中，导数就是函数的变化率。对于二元函数研究它的“变化率”，由于自变量多了一个，情况就要复杂的多。
在xy平面内，当动点由 P(x0,y0) 沿不同方向变化时，函数 f(x,y) 的变化快慢一般来说是不同的，因此就需要研究 f(x,y) 在 (x0,y0) 点处沿不同方向的变化率。
在这里我们只学习函数 f(x,y) 沿着平行于 x 轴和平行于 y 轴两个特殊方位变动时， f(x,y) 的变化率。
偏导数的表示符号为:∂。
偏导数反映的是函数沿坐标轴正方向的变化率。

2.2 定义

x方向的偏导
设有二元函数 z=f(x,y) ，点(x0,y0)是其定义域D 内一点。把 y 固定在 y0而让 x 在 x0 有增量 △x ，相应地函数 z=f(x,y) 有增量（称为对 x 的偏增量）△z=f(x0+△x,y0)-f(x0,y0)。
如果 △z 与 △x 之比当 △x→0 时的极限存在，那么此极限值称为函数 z=f(x,y) 在 (x0,y0)处对 x 的偏导数，记作 f’x(x0,y0)或。函数 z=f(x,y) 在(x0,y0)处对 x 的偏导数，实际上就是把 y 固定在 y0看成常数后，一元函数z=f(x,y0)在 x0处的导数。
y方向的偏导
同样，把 x 固定在 x0，让 y 有增量 △y ，如果极限存在那么此极限称为函数 z=(x,y) 在 (x0,y0)处对 y 的偏导数。记作f’y(x0,y0)。

2.3 求法

当函数 z=f(x,y) 在 (x0,y0)的两个偏导数 f’x(x0,y0) 与 f’y(x0,y0)都存在时，我们称 f(x,y) 在 (x0,y0)处可导。如果函数 f(x,y) 在域 D 的每一点均可导，那么称函数 f(x,y) 在域 D 可导。
此时，对应于域 D 的每一点 (x,y) ，必有一个对 x (对 y )的偏导数，因而在域 D 确定了一个新的二元函数，称为 f(x,y) 对 x (对 y )的偏导函数。简称偏导数。
按偏导数的定义，将多元函数关于一个自变量求偏导数时，就将其余的自变量看成常数，此时他的求导方法与一元函数导数的求法是一样的。

2.4 几何意义

表示固定面上一点的切线斜率。
偏导数 f’x(x0,y0) 表示固定面上一点对 x 轴的切线斜率；偏导数 f’y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。
高阶偏导数：如果二元函数 z=f(x,y) 的偏导数 f’x(x,y) 与 f’y(x,y) 仍然可导，那么这两个偏导函数的偏导数称为 z=f(x,y) 的二阶偏导数。二元函数的二阶偏导数有四个：f"xx，f"xy，f"yx，f"yy。
注意：
f"xy与f"yx的区别在于：前者是先对 x 求偏导，然后将所得的偏导函数再对 y 求偏导；后者是先对 y 求偏导再对 x 求偏导。当 f"xy 与 f"yx 都连续时，求导的结果与先后次序无关。

3.矩阵

有关矩阵的知识内容，我建议大家还是直接去查看线性带书这本书比较好，书中案例比较多，更方便大家理解。
以下为我手中的同济大学-线性代数第六版目录中的前三章内容，按照目前我的体验来看，读取第一章行列式之后，再结合一些矩阵求导法则就可以解决一些基础相关问题了。

3.1矩阵运算

3.1.1 矩阵加

3.1.2数与矩阵相乘

3.1.3矩阵与矩阵相乘

3.2矩阵求导法则

写在前面：数学中的向量默认是行向量，但机器学习中的向量默认都是列向量。因此后期不要和搞混。

矩阵求导应该分为标量求导、向量求导、矩阵求导三个方面来介绍，公式繁多，但仔细看看其实是有规律可循的。

3.2.1标量求导

无论是矩阵、向量对标量求导，或者是标量对矩阵、向量求导，其结论都是一样的：等价于对矩阵（向量）的每个分量求导，并且保持维数不变。

例如，我们可以计算标量对向量求导：

3.2.2向量求导

对于向量求导，我们可以先将向量看做一个标量，然后使用标量求导法则，最后将向量形式化为标量进行。

例如，我们可以计算行向量对列向量求导：

3.2.3矩阵求导

与向量求导类似，先将矩阵化当做一个标量，再使用标量对矩阵的运算进行。

例如，我们可以计算矩阵对列向量求导：

这部分内容引用这篇博客https://blog.csdn.net/crazy_scott/article/details/80557814
其他具体详细的一些可以参考：维基百科矩阵求导公式。链接为：https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities

3.3 推导线性回归时所需的矩阵求导公式

推导线性回归时需要使用到的矩阵求导公式为：

大家下去可以自行退导。

4.对数

概念部分的内容我直接截取自百度百科。

4.1对数符号

4.2对数的定义

4.3对数运算法则

这个是后期公式推导时需要使用的。

以上为基本上为需要准备的基础知识了，后期准备分享有关具体线性回归的推导过程。以上内容如果有什么问题欢迎大家批评指正。