TensorFlow：机器学习基础

目录

  在这本次实验中，我们将概述TensorFlow的基础知识，        
  了解它的结构并查看使用它的动机
   TensorFlow如何工作？
    建立一个图表
    使用TensorFlow定义多维数组
    为什么要测量张量？
       变量
      占位符
      操作
     练习题

TensorFlow如何工作？

TensorFlow在不同设备（如CPU和GPU）上执行代码的能力是其特定结构的结果：

TensorFlow将计算定义为图形，并且这些都是用操作（也称为“ops”）进行的。所以，当我们使用TensorFlow时，它就像在Graph中定义一系列操作一样。

要将这些操作作为计算来执行，我们必须将图形启动到会话中。会话会将表示到图表中的操作转换并传递到要执行它们的设备，无论是GPU还是CPU。

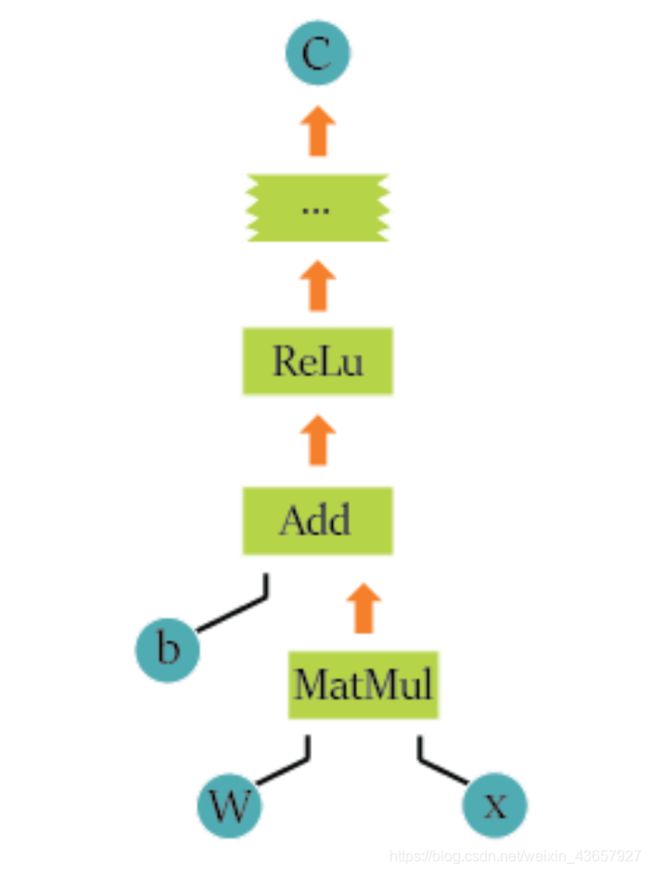
例如，下面的图片表示TensorFlow中的图形。W, x 和b是这个图的边上的张量。MatMul 是对张量W 和x的一个操作，之后调用 _Add_并将前一个运算符的结果与 b相加。每个操作的合成张量与下一个操作相交，直到可能获得所需结果的结束。

导入 TensorFlow

要使用TensorFlow，我们需要导入库。我们导入了它，并且可选地给它命名为"tf"，所以模块可以通过__tf.module-name__访问：

import tensorflow as tf

构建图表

正如我们之前所说的，TensorFlow是一个图形计算模型。我们来创建我们的第一个图。

为了创建我们的第一个图形，我们将利用源操作，它不需要任何信息输入。这些源操作或source ops将把它们的信息传递给执行计算的其他操作。

要创建两个输出数字的源操作，我们将定义两个常量：

           a = tf.constant([2])
           b = tf.constant([3])

之后，让我们对这些变量进行操作。函数 tf.add()添加了两个元素（您也可以使用 c = a + b）。

 c = tf.add(a,b)
 #c = ab + b也是进行加法的一种计算方式

然后TensorFlow需要初始化一个会话来运行我们的代码。在某种程度上，会话是在TensorFlow中创建图形的上下文。让我们来定义我们的会话：

 session = tf.Session()

让我们运行会话以获取来自之前定义的c操作的结果：

       result = session.run(c)
       print(result)

关闭会话以释放资源:

    session.close()

为了避免每一次关闭会话，我们可以在一个with块中定义它们，所以运行with块后会话将自动关闭：

 with tf.Session() as session:
       result = session.run(c)
       print(result)

即使添加2个常量来达到简单结果，这个愚蠢的例子也定义了TensorFlow的基础。定义你的边缘（在这种情况下，我们的常量），包括节点（操作，如t_tf.add_），并启动一个会话来构建图形。

Tensor含义是什么？

在TensorFlow中，所有数据都在计算图中的操作之间传递，这些数据以Tensors的形式传递，因此称为TensorFlow。

新拉丁词__tensor__意思是“延伸”。这是一个名为__tensor__的数学对象， 因为张量的早期应用就是研究在张力下拉伸的材料。张量的当代意义可以看作多维阵列。 

这很好，但是…这些多维数组是什么？
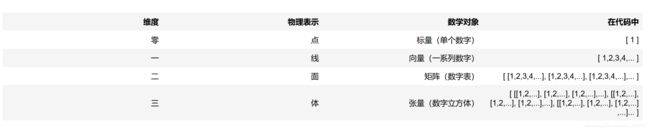
回顾一下物理学理解维度的概念：
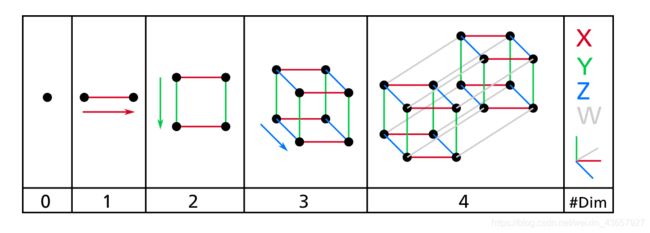零维可以被看作是一个点，一个单一的对象或一个单一的项目。

第一个维度可以看作一条线，一维数组可以看作是沿着这条线的数字，或者沿着这条线的点。一个维度可以包含无限的零维/点元素。

第二个维度可以被看作是一个表面，一个二维数组可以被看作是沿无限长线条的无限系列。

第三维可以看作是体积，三维阵列可以看作是沿着无限长线的无限系列表面。

第四维可以被看作是超空间或时空，体积随着时间的变化而变化，或者是无穷大的无限系列。等等…

作为数学对象：

总结：

使用TensorFlow定义多维数组

现在我们将尝试使用TensorFlow定义这样的数组：

Scalar = tf.constant([2])
Vector = tf.constant([5,6,2])
Matrix = tf.constant([[1,2,3],[2,3,4],[3,4,5]])
Tensor = tf.constant( [ [[1,2,3],[2,3,4],[3,4,5]] , [[4,5,6],          [5,6,7],[6,7,8]] , [[7,8,9],[8,9,10],[9,10,11]] ] )
with tf.Session() as session:
      result = session.run(Scalar)
      print ("Scalar (1 entry):\n %s \n" % result)
      result = session.run(Vector)
      print ("Vector (3 entries) :\n %s \n" % result)
      result = session.run(Matrix)
      print ("Matrix (3x3 entries):\n %s \n" % result)
      result = session.run(Tensor)
      print( "Tensor (3x3x3 entries) :\n %s \n" % result)

现在你已经理解了这些数据结构，我鼓励你使用一些以前的函数来玩这些数据结构，根据它们的结构类型来看看它们的行为方式：

Matrix_one = tf.constant([[1,2,3],[2,3,4],[3,4,5]])
Matrix_two = tf.constant([[2,2,2],[2,2,2],[2,2,2]])

first_operation = tf.add(Matrix_one, Matrix_two)
second_operation = Matrix_one + Matrix_two

with tf.Session() as session:
      result = session.run(first_operation)
      print ("Defined using tensorflow function :")
      print(result)
      result = session.run(second_operation)
      print( "Defined using normal expressions :")
      print(result)

使用常规符号定义和TensorFlow函数，我们可以获得元素乘法，也称为Hadamard乘积。

但是如果我们想要常规矩阵产品呢？

然后我们需要使用另一个称为 tf.matmul()的 TensorFlow函数：

Matrix_one = tf.constant([[2,3],[3,4]])
Matrix_two = tf.constant([[2,3],[3,4]])

first_operation = tf.matmul(Matrix_one, Matrix_two)

with tf.Session() as session:
    result = session.run(first_operation)
    print ("Defined using tensorflow function :")
    print(result)  

我们也可以自己定义这个乘法，但是有一个函数已经做到了，所以不需要重新发明轮子！

为什么叫Tensors?

Tensors结构通过给我们想要的方式自由地塑造数据集来帮助我们。

由于图像信息如何编码的性质，在处理图像时特别有用，

考虑到图像，它很容易理解它具有高度和宽度，因此用二维结构（矩阵）表示图像中包含的信息是有意义的…直到您记住图像具有颜色，并且添加关于颜色的信息，我们需要另一个维度，那么当张量变得特别有用时。

图像被编码到彩色通道中，图像数据在给定点处被表示为颜色通道中的每种颜色强度，最常见的是RGB，这意味着红色，蓝色和绿色。包含在图像中的信息是每个通道颜色在图像宽度和高度上的强度，就像这样：

因此，每个具有宽度和高度的点处的红色通道的强度可以表示为矩阵，对于蓝色和绿色通道也是如此，所以我们最终得到三个矩阵，并且当它们结合时它们形成张量。

变量

现在我们更熟悉数据的结构，我们将看看TensorFlow如何处理变量。

要定义变量，我们使用命令tf.variable()。为了能够在计算图中使用变量，有必要在会话中运行图之前对它们进行初始化。这是通过运行tf.global_variables_initializer()来完成的。

要更新变量的值，我们只需运行一个赋值给变量的赋值操作：

      state = tf.Variable(0)

我们首先创建一个简单的计数器，一次增加一个单位的变量：

 one = tf.constant(1)
 new_value = tf.add(state, one)
 update = tf.assign(state, new_value)

变量必须在启动图形后通过运行初始化操作来初始化。我们首先必须将初始化操作添加到图中：

 init_op = tf.global_variables_initializer()

然后我们开始一个会话来运行图形，首先初始化变量，然后打印state 变量的初始值，然后运行更新state 变量并在每次更新后打印结果的操作：

with tf.Session() as session:
    session.run(init_op)
    print(session.run(state))
    for _ in range(3):
       session.run(update)
       print(session.run(state))

占位符

现在我们知道如何操作TensorFlow中的变量，但是如何在TensorFlow模型外部提供数据呢？

如果要将数据从模型外部提供给TensorFlow模型，则需要使用占位符。

那么这些占位符是什么，他们做了什么？

占位符可以被看作是模型中的"洞"，您将传递数据到的"洞"，您可以使用
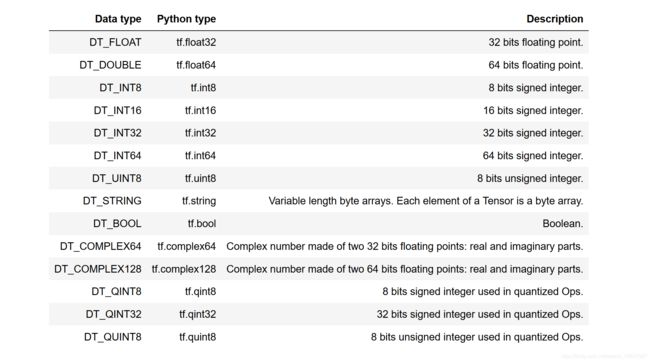
tf.placeholder(datatype)创建它们，其中数据类型指定_datatype_ （整数，浮点数，字符串，布尔值）以及其精度（8,16,32,64）位。

每个数据类型的定义与相应的python sintax定义如下：

所以我们创建一个占位符：

a=tf.placeholder(tf.float32)

并定义一个简单的乘法运算：

          b=a*2

传递给数据，否则我们会得到一个错误。

为了将数据传递给模型，我们使用额外参数 feed_dict调用会话，在该参数中我们应该传递一个字典，其中每个占位符名称都由其各自的数据覆盖，如下所示：

 with tf.Session() as sess:
     result = sess.run(b,feed_dict={a:3.5})
     print(result)

由于TensorFlow中的数据是以多维数组的形式传递的，我们可以通过占位符传递任何类型的张量以获得简单乘法操作的答案：

dictionary={a: [ [ [1,2,3],[4,5,6],[7,8,9],[10,11,12] ] , [ [13,14,15],[16,17,18],[19,20,21],[22,23,24] ] ] }

with tf.Session() as sess:
    result = sess.run(b,feed_dict=dictionary)
    print(result)

操作

操作是表示图上张量的数学运算的节点。这些操作可以是任何类型的函数，如加减张量或者激活函数。

tf.matmul_, tf.add, _tf.nn.sigmoid 是TensorFlow中的一些操作。这些就像python中的函数，但是直接在张量上运行，并且每个都执行特定的事情。

a = tf.constant([5])
b = tf.constant([2])
c = tf.add(a,b)
d = tf.subtract(a,b)

with tf.Session() as session:
    result = session.run(c)
     print ('c =: %s' % result)
     result = session.run(d)
     print ('d =: %s' % result)

_tf.nn.sigmoid_是一个激活函数，它有点复杂，但是这个函数有助于学习模型来评估哪种信息是好的或者不是。

练习题

在这之前，让我们导入TensorFlow库

  %matplotlib inline
  import tensorflow as tf

首先，尝试添加两个常量并打印结果。

     a = tf.constant([5])
     b = tf.constant([2])

练习 1:
使用sum（+）操作创建另一个TensorFlow对象

c=a+b
c=tf.add(a,b)

with tf.Session() as session:
    result = session.run(c)
    print ("The addition of this two constants is: {0}".format(result))

练习 2:
现在让我们尝试将它们相乘

c=a*b
c=tf.multiply(a,b)

with tf.Session() as session:
     result = session.run(c)
     print( "The Multiplication of this two constants is: {0}".format(result))

练习 3:
乘法：单元乘法或矩阵乘法
让我们练习乘法矩阵的不同方法：
第一个操作中的元素方式乘法;
第一个操作中的矩阵方式乘法 ;

matrixA = tf.constant([[2,3],[3,4]])
matrixB = tf.constant([[2,3],[3,4]])

first_operation=tf.multiply(matrixA, matrixB) second_operation=tf.matmul(matrixA,matrixB)

with tf.Session() as session:
    result = session.run(first_operation)
    print ("Element-wise multiplication: \n", result)

    result = session.run(second_operation)
    print ("Matrix Multiplication: \n", result)

练习 4:
将变量b的值修改为常量a中的值：

a=tf.constant(1000)
b=tf.Variable(0)
init_op = tf.global_variables_initializer()

a=tf.constant(1000) b=tf.Variable(0) init_op = tf.global_variables_initializer() update = tf.assign(b,a) with tf.Session() as session: session.run(init_op) session.run(update) print(session.run(b))

练习 5:
斐波那契序列
现在尝试做更先进的事情。尝试创建一个斐波那契序列并使用TensorFlow输出前几个值 如果你不知道，斐波那契序列由下面的公式定义:
=−1+−2
产生如下序列：1,1,2,3,5,8,13,21 …

a=tf.Variable(0) b=tf.Variable(1) temp=tf.Variable(0)     c=a+b

update1=tf.assign(temp,c) update2=tf.assign(a,b) update3=tf.assign(b,temp)

init_op = tf.initialize_all_variables() with tf.Session() as s: s.run(init_op) for _ in range(15): 
print(s.run(a)) s.run(update1) s.run(update2) s.run(update3)

f = [tf.constant(1),tf.constant(1)] for i in range(2,10): temp = f[i-1] + f[i-2] f.append(temp) with tf.Session() as sess: result = sess.run(f) print(result)

练习 6:
现在尝试创建您自己的占位符并定义它们之间的任何类型的操作：

   a=tf.placeholder(tf.float32) b=tf.placeholder(tf.float32)

   c=2*a -b

   dictionary = {a:[2,2],b:[3,4]} with tf.Session() as   session:
   print(session.run(c,feed_dict=dictionary)) 

尝试改变我们的例子与其他一些操作，并看到结果。
函数的一些例子：
tf.multiply(x, y)
tf.div(x, y)
tf.square(x)
tf.sqrt(x)
tf.pow(x, y)
tf.exp(x)
tf.log(x)
tf.cos(x)
tf.sin(x)

a = tf.constant(5.)
b = tf.constant(2.)

练习 7:
创建一个变量，命名c` 为接收结果的操作（看你的选择）：

  c=tf.sin(a)
  with tf.Session() as session:
      result = session.run(c)
      print ("c =: {}".format(result))

它们与数学函数非常相似，唯一的区别是操作在tensors上运行。