美赛整理之投影寻踪模型及其求解
投影寻踪模型
-
- 1.模型的简介和应用
- 2.基本步骤:
- 3.遗传算法求解模型的优化问题
-
- 1.用 M a t l a b Matlab Matlab的 g a ga ga工具箱求解:
- 2.遗传算法求解:
- 3. L I N G O LINGO LINGO求解
1.模型的简介和应用
投影寻踪是处理和分析高维数据的一类统计方法,其基本思想是将高维数据投影到低维(1~3维)子空间上,寻找出反映原高维数据的结构或特征的投影,以达到研究和分析高维数据的目的。1974年,美国Stanford大学的Friedman和Tukey首次将该方法命名为Projection Pursuit,即投影寻踪。
投影寻踪(projection pursuit,简称PP)是国际统计界于70年代中期发展起来的一种新的、有价值的新技术,是统计学、应用数学和计算机技术的交叉学科。它是用来分析和处理高维观测数据,尤其是非正态非线性高维数据的一种新兴统计方法。它通过把高维数据投影到低维子空间上,寻找出能反映原高维数据的结构或特征的投影,达到研究分析高维数据的目的。它具有稳健性、抗干扰性和准确度高等优点,因而在许多领域得到广泛应用。
从投影寻踪的理论与应用研究来看,主要涉及三方面内容:
1.投影寻踪聚类分析;
2.投影寻踪回归;
3.投影寻踪学习网络。
2.基本步骤:
设第 i i i个样本的第 j j j个指标为 x i j ( i = 1 , 2.. n , j = 1 , 2.. m ) x_{ij}(i=1,2..n,j = 1,2..m) xij(i=1,2..n,j=1,2..m), n n n为样本个数, m m m为指标个数。投影寻踪模型建立的投影寻踪聚类模型的步骤如下。
1.样本数据归一化:
x i j ‘ = x i j − x j , m i n x j , m a x − x j , m i n x_{ij}^{`} = \frac{x_{ij}-x_{j,min}}{x_{j,max}-x_{j,min}} xij‘=xj,max−xj,minxij−xj,min
2.线性投影:
从不同的角度去观察数据,寻找最能挖掘数据大的最优投影方向。随机抽取若干初始投影方向 a ( a 1 , a 2 , . . . , a m ) a(a_1,a_2,...,a_m) a(a1,a2,...,am),计算其投影指标的大小。确定最大指标的投影的解为其最佳投影方向:
样本 i i i在一维空间的投影方向为 ( a 1 , a 2 , . . . a m ) (a_1,a_2,...a_m) (a1,a2,...am)上的投影特征值定义为:
z i = ∑ j = 1 m a j x i j z_i = \sum_{j = 1}^{m} a_jx_{ij} zi=j=1∑majxij
3.寻找目标函数:
要求 z i z_i zi的为:局部投影点尽可能集中,形成许多的点团。整体上尽可能散开。
定义目标函数为 Q ( a ) Q(a) Q(a),类间距离为 s ( a ) s(a) s(a),类内密度为 d ( a ) d(a) d(a)。那么:
Q ( a ) = s ( a ) d ( a ) Q(a) = s(a)d(a) Q(a)=s(a)d(a)
类间距离用样本序列的投影特征值方差计算:
s ( a ) = 1 n ∑ i = 1 n ( z i − 1 n ∑ i = 1 n z i ) 2 i = 1 , 2... n s(a) = \sqrt{\frac{1}{n}\sum_{i = 1}^n(z_i - \frac{1}{n}\sum_{i = 1}^nz_i)^2}\\ i = 1,2...n s(a)=n1i=1∑n(zi−n1i=1∑nzi)2i=1,2...n
投影特征值间的距离为 r i k = ∣ z i − z k ∣ ( i , k = 1 , 2 , . . . n ) r_{ik} = |z_i - z_k|(i,k = 1,2,...n) rik=∣zi−zk∣(i,k=1,2,...n),那么:
d ( a ) = ∑ i = 1 n ∑ k = 1 n ( R − r i k ) f ( R − r i k ) d(a) = \sum_{i = 1}^n\sum_{k = 1}^n(R - r_{ik})f(R - r_{ik}) d(a)=i=1∑nk=1∑n(R−rik)f(R−rik)
其中的 f ( t ) f(t) f(t)为以阶跃信号:
f ( t ) = { 0 , t < 0 1 , t ≥ 0 f(t)= \begin{cases}0,t<0\\1,t \geq 0 \end{cases} f(t)={0,t<01,t≥0
R R R为估计局部散点密度的窗宽参数,按宽度内至少包括一个散点的原则,其值与样本数据结构有关:
m a x ( r i k ) < R < 2 m i , k = 1 , 2 , . . . n max(r_{ik})
4.优化投影方向:
将寻找最优投影方向问题转化为下列优化问题:
m a x Q ( a ) = s ( a ) d ( a ) ∑ j = 1 m a j 2 = 1 maxQ(a) = s(a)d(a)\\ \sum_{j = 1}^ma_j^2 = 1 maxQ(a)=s(a)d(a)j=1∑maj2=1
可用遗传算法优化。
5.综合评价聚类分析:
以 z i z_i zi的差异水平对样本群进行聚类分析。根据最优投影方向,便可计算反应各评价指标综合信息的投影特征值 z i z_i zi的差异水平。求出最优投影系数 a = a ( a 1 , a 2 , . . . a m ) a = a(a_1,a_2,...a_m) a=a(a1,a2,...am)。
3.遗传算法求解模型的优化问题
1.用 M a t l a b Matlab Matlab的 g a ga ga工具箱求解:
调用 M a t l a b Matlab Matlab的遗传算法工具箱。
[ x , f v a l ] = g a ( @ f i t n e s s , n v a r s , A , b , A e q , b e q , L B , U B , @ n o n l c o n , o p t i o n s ) ; [x,fval] = ga(@fitness,nvars,A,b,Aeq,beq,LB,UB,@nonlcon,options); [x,fval]=ga(@fitness,nvars,A,b,Aeq,beq,LB,UB,@nonlcon,options);
其中 x x x为决策向量, f i t n e s s fitness fitness为适应度函数 f i t n e s s ( x ) fitness(x) fitness(x), n v a r s nvars nvars:代表决策向量 x x x的个数,其中 A , b , A e q , b e q , L B , U B A,b,Aeq,beq,LB,UB A,b,Aeq,beq,LB,UB满足以下关系:
A x ≤ b A e q × x ≤ b e q L B ≤ x ≤ U B Ax \leq b\\ Aeq \times x \leq beq\\ LB\leq x \leq UB\\ Ax≤bAeq×x≤beqLB≤x≤UB
其中 [ f , g ] = n o n l c o n ( x ) [f,g] = nonlcon(x) [f,g]=nonlcon(x),且 f f f为非线性不等式约束, g g g为非线性等式约束:
f ( x ) ≤ 0 g ( x ) = 0 f(x)\leq 0\\ g(x) = 0 f(x)≤0g(x)=0
而很多时候其实我们如果有非线性等式约束的话是很难直接找到合适的解的,或者说要花很长时间。这是我们可以设定一个阈值 δ \delta δ,使得:
0 ≤ g ( x ) ≤ δ 0 \leq g(x) \leq \delta 0≤g(x)≤δ
来大概满足我们的求解要求。那么此时就可以把等式约束化为不等式约束:
f = ( − g ( x ) g ( x ) − δ ) f = \begin{pmatrix} -g(x)\\g(x)-\delta\end{pmatrix} f=(−g(x)g(x)−δ)
通过这种手段尽可能搜索最优解。相关的matlab代码如下:
归一化代码:
function [z,xd] = normalizef( x,a )
%UNTITLED6 此处显示有关此函数的摘要
% 此处显示详细说明
% [n1,m1]= size(a);%默认是一行m1列
[n,m] = size(x);
x_min = zeros(1,m);
x_max = zeros(1,m);
z = zeros(1,n);
for j = 1:m
x_min(j) = min(x(:,j));
x_max(j) = max(x(:,j));
end
for i = 1:n
for j = 1:m
xd(i,j) = (x(i,j)-x_min(j))/(x_max(j)-x_min(j));
end
end
for i = 1:n
sum = 0;
for j = 1:m
sum = sum + a(j)*xd(i,j);
end
z(i) = sum;
end
end
求 S ( a ) S(a) S(a)的代码:
function S_a = S(z)
%UNTITLED2 此处显示有关此函数的摘要
% 此求S(a)
[m,n] = size(z);%默认为是一行n列
z_mean = sum(z)/n;
S_a = sqrt( 1/n*(sum((z-z_mean).^2)) );
end
求 D ( a ) D(a) D(a)的代码:
function da = D(z)
%UNTITLED4 此处显示有关此函数的摘要
% 求d(a),我们假定R = r_m+3;
[m,n] = size(z);%默认为是一行n列
sum = 0;
for i = 1:n
for k = 1:n
r(i,k) = abs(z(i)-z(k));
% sum = sum+(R-r(i,k))*fun(R-r(i,k));
end
end
R = max(max(r));
R = R+3;
for i = 1:n
for k = 1:n
sum = sum+(R-r(i,k))*fun(R-r(i,k));
end
end
da = sum;
end
函数 f ( x ) f(x) f(x)的代码:
function f = fun( t )
%UNTITLED5 此处显示有关此函数的摘要
% 此处显示详细说明
if t>=0
f =1;
else
f = 0;
end
end
适应度函数代码:
function Q = fitness(a)
%UNTITLED8 此处显示有关此函数的摘要
% 用遗传算法求最优的 a (适应度函数)
x = xlsread('数据.xlsx','sheet1','B2:N9');
[z,xd] = normalizef( x,a );
Q = S(z)*D(z);
Q = -Q;
end
约束函数代码:
function [ f,g ] = yueshu( a )
%UNTITLED10 此处显示有关此函数的摘要
% 此处显示详细说明
%[n,m] = size(a);
delta = 0.1;
f = [1-sum(a.^2);sum(a.^2)-1-delta;];
g= [];
end
主函数代码:
%主函数用遗传算法求解最合适的投影角度
nvars = 13;
a = sqrt(1/13)*ones(1,nvars);
options = gaoptimset('PopulationSize',50,'Generations',20,'PlotFcns',@gaplotbestf);
[a fval] = ga(@fitness,nvars,[],[],[],[],[],[],@yueshu,options);
fval = -fval;
disp('最终的a是:');
disp(a);
disp('目标函数值是:');
disp(fval);
结果是:
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
and constraint violation is less than options.ConstraintTolerance.
最终的a是:
-0.1534 0.2417 -0.0865 0.7742 -0.0963 -0.0297 0.2373 0.3051 -0.3150 0.3357 -0.0384 0.0405 -0.0820
经过验证得到:
sum(a.^2)
ans =
1.0702
数据暂不给出
遗传算法工具箱的优化的确有点复杂,后面将直接用遗传算法来优化。
2.遗传算法求解:
如果用遗传算法求解的话最重要的就是要有一个函数能产生满足约束条件 ∑ i = 1 m a i 2 = 1 \sum_{i=1}^ma_i^2=1 ∑i=1mai2=1的解 ( a 1 , a 2 , . . . a m ) (a_1,a_2,...a_m) (a1,a2,...am)。现在就将这样的满足约束条件的赋值函数给出:
function al = inital(nvars,N,step)
%nvars = 13;
%N = 10000;决定最后样本个数的次数
%step = 0.1;划分步长
al = [];
k = 0;
for alpha = 0:step:1
for k=1:N
a = zeros(1,nvars);
k = k+1;
for i = 1:(nvars-1)
a(i) = rand*(1-alpha);
end
sum_n_1 = sum(a(1:(nvars-1)).^2);
if sum_n_1>1
continue;
else
a(nvars) = sqrt(1- sum_n_1);
al = [al;a];
end
end
end
% [m,n] = size(al);
% for j = 1:100
% Q(j) = fitness(al(j,:));
% end
% plot(1:100,Q);
end
这个算法的主要思想是用不同比例的 [ 0 , 1 ] [0,1] [0,1]的均匀随机数用来填充 ( a 1 , a 2 , . . . a m − 1 ) (a_1,a_2,...a_{m-1}) (a1,a2,...am−1),然后根据这 m − 1 m-1 m−1组数据求出 a m a_m am。这样就可以求出满足约束条件 ∑ i = 1 m a i 2 = 1 \sum_{i=1}^ma_i^2=1 ∑i=1mai2=1的很多样本。然后由大数定律可以求出,最后实际满足要求的样本个数约为 N 2 s t e p \frac{N}{2step} 2stepN。
剩下的遗传算法的其他实现过程就不再赘述。
取前 100 100 100组数据观察这些数据的适应度为:
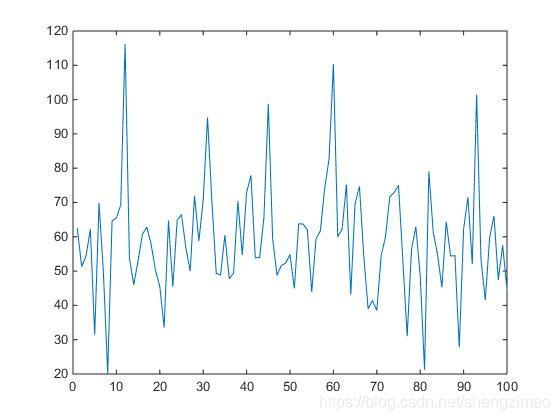
3. L I N G O LINGO LINGO求解
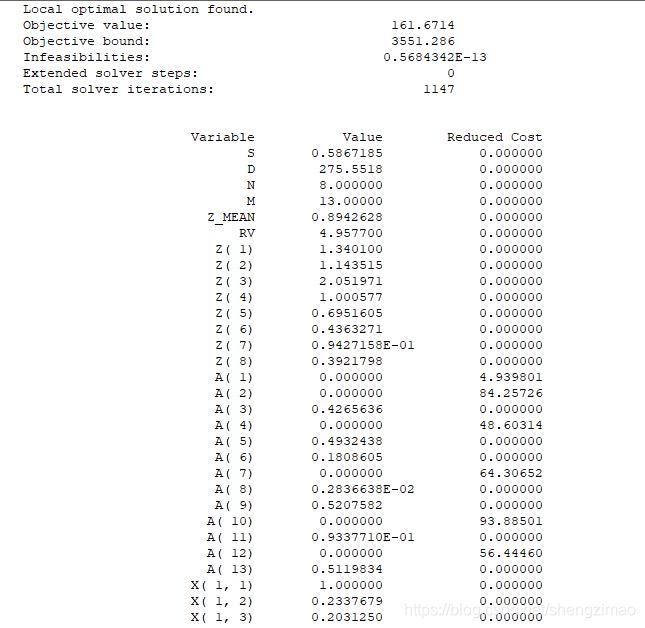
若将归一化后的数据存入 数 据 2. x l s x 数据2.xlsx 数据2.xlsx的 d a t a data data区域后,调用 L I N G O LINGO LINGO求解:
model:
sets:
row/1..8/:z;
col/1..13/:a;
link(row,col):x;
same(row,row):r;
endsets
data:
x = @ole('D:\LINGO11\数据2.xlsx',data2);
enddata
max = s*d;
n = @size(row);
m = @size(col);
@for(row(i):z(i)=@sum(col(j):a(j)*x(i,j)));
z_mean = 1.0/n*@sum(row(i):z(i));
s = @sqrt(1.0/n*@sum(row(i):(z(i)-z_mean)^2));
@for(same(i,k):r(i,k)=@abs(z(i)-z(k)));
Rv = @max(same(i,k):r(i,k))+3;
d = @sum(same(i,k):(Rv-r(i,k))*@if((Rv-r(i,k))#ge#0,1,0));
@sum(col(j):(a(j))^2) = 1;
end