基于强化学习的多战机同SEAD联合作战空战辅助决策(改进版)
基于强化学习的多战机同SEAD联合作战空战辅助决策(改进版)
1.基础知识
这部分的基础知识可以参考以前的博文:基于强化学习的多战机同SEAD联合作战空战辅助决策
2.之前的工作
之前运用强化学习的知识求解时,对其的建模分为以下几个部分:
-
状态空间:两个战机的状态,分别是两个战机的横纵坐标:
s t = ( x 1 ( t ) , y 1 ( t ) , x 2 ( t ) , y 2 ( t ) ) T ∈ [ 0 , 100 k m ] 4 s_t=(x_1^{(t)},y_1^{(t)},x_2^{(t)},y_2^{(t)})^T\in [0,100\mathbf {km}]^4 st=(x1(t),y1(t),x2(t),y2(t))T∈[0,100km]4 -
动作空间:两个战机彼此的动作空间看作是相同的,其联合动作空间为:
a t ∈ { 东 , 正东北 , 北 , 正西北 , 西 , 正西南 , 南 , 正东南 , 停留 } ( 1 ) × { 东 , 正东北 , 北 , 正西北 , 西 , 正西南 , 南 , 正东南 , 停留 } ( 2 ) a_t\in \{东,正东北,北,正西北,西,正西南,南,正东南,停留\}^{(1)} \times \{东,正东北,北,正西北,西,正西南,南,正东南,停留\}^{(2)} at∈{东,正东北,北,正西北,西,正西南,南,正东南,停留}(1)×{东,正东北,北,正西北,西,正西南,南,正东南,停留}(2)
实际上 a t a_t at的维度是2,例如: a t = ( 东 , 正西北 ) T a_t=(东,正西北)^T at=(东,正西北)T表示的是第t时刻,战机1采取向正东匀速运动时间段 Δ t \Delta t Δt,战机2采取向正西北匀速运动时间段 Δ t \Delta t Δt。所以实际的动作空间中的离散动作个数为 9 × 9 = 81 9 \times 9=81 9×9=81。例如采取这样的动作下一个状态的转移方程为:
x 1 ( t + 1 ) = x 1 ( t ) + v 1 Δ t y 1 ( t + 1 ) = y 1 ( t ) x 2 ( t + 1 ) = x 2 ( t ) − 2 2 v 2 Δ t y 2 ( t + 1 ) = y 2 ( t ) + 2 2 v 2 Δ t x_{1}^{(t+1)} =x_{1}^{(t)} +v_1 \Delta t \\ y_1^{(t+1)}=y_1^{(t)}\\ x_{2}^{(t+1)} =x_{2}^{(t)} -\frac{\sqrt{2}}{2}v_2 \Delta t \\ y_{2}^{(t+1)} =y_{2}^{(t)} +\frac{\sqrt{2}}{2}v_2 \Delta t \\ x1(t+1)=x1(t)+v1Δty1(t+1)=y1(t)x2(t+1)=x2(t)−22v2Δty2(t+1)=y2(t)+22v2Δt
-
奖励函数:
奖励函数主要有以下几种情况:
- 当战机1,2其中任意一架击毁Target时,返回奖励1000,回合结束。
- 当战机1,2其中一架在SAM的火力范围内停留时间超过SAM的火力瞄准时间时,任意一架战机被摧毁都会返回奖励-1000,回合继续。直到两架战机都被摧毁回合结束。
- 当SAM在战机1,2其中的一架火力范围内停留时间超过战机的火力瞄准时间时,SAM会被摧毁,此时返回奖励50,回合继续。
- 其他情况,每经历一个时间段,返回奖励-1,回合继续。
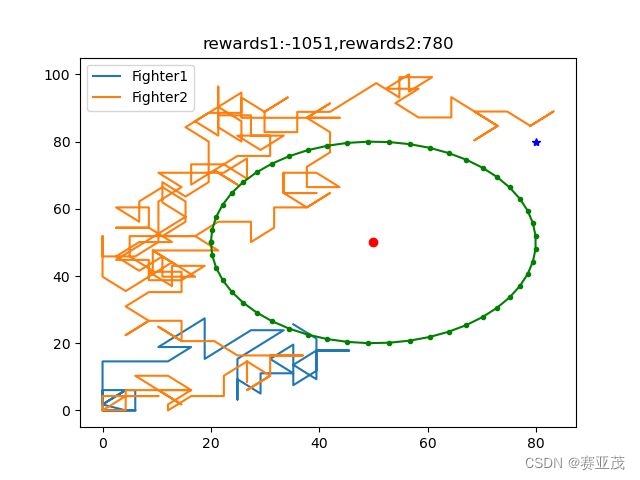
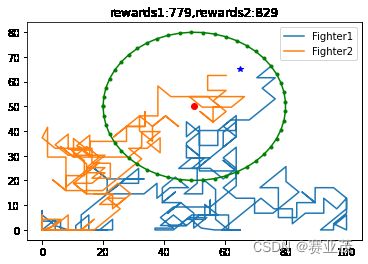
当采取以上参数时,得用PPO训练的两组较为优化的轨迹如下:
实际上这里的描述是不对的,因此从实际的角度考虑,战斗机的转向角度不会这么大。过大的转向角度(最小45°)使得战机的轨迹类似于随机游走,几乎是醉汉走路。
3.现在的工作
在之前的工作的基础上,仅仅修改战机的状态空间与动作空间。在不考虑修改原来的奖励函数的基础上,在状态空间中引入两个战机的二维方位角 θ t ( 1 ) , θ t ( 2 ) \theta_t^{(1)},\theta_t^{(2)} θt(1),θt(2)。而将动作空间修改为两个战机在 t t t时刻方位角的增量值 Δ θ t ( 1 ) , Δ θ t ( 2 ) \Delta \theta_t^{(1)},\Delta \theta_t^{(2)} Δθt(1),Δθt(2)。如下所示:
-
状态空间:两个战机的状态,分别是两个战机的横纵坐标以及方位角:
s t = ( x t ( 1 ) , y t ( 1 ) , θ t ( 1 ) , x t ( 2 ) , y t ( 2 ) , θ t ( 2 ) ) T ∈ [ 0 , 100 k m ] 2 × [ − π , π ] × [ 0 , 100 k m ] 2 × [ − π , π ] s_t=(x_t^{(1)},y_t^{(1)},\theta_t^{(1)},x_t^{(2)},y_t^{(2)},\theta_t^{(2)})^T\in [0,100\mathbf {km}]^2 \times [-\pi,\pi] \times [0,100\mathbf {km}]^2\times [-\pi,\pi] st=(xt(1),yt(1),θt(1),xt(2),yt(2),θt(2))T∈[0,100km]2×[−π,π]×[0,100km]2×[−π,π] -
动作空间:两个战机可以采取的二维方位角的增量:
a t = [ Δ θ t ( 1 ) , Δ θ t ( 2 ) ] ∈ { − π 12 , π 12 } ( 1 ) × { − π 12 , π 12 } ( 2 ) a_t=[\Delta \theta_t^{(1)},\Delta \theta_t^{(2)}]\in\{-\frac{\pi}{12},\frac{\pi}{12}\}^{(1)} \times \{-\frac{\pi}{12},\frac{\pi}{12}\}^{(2)} at=[Δθt(1),Δθt(2)]∈{−12π,12π}(1)×{−12π,12π}(2)
很明显,这里的动作空间是连续动作空间。再次为了方便用离散PPO算法进行求解,将上述连续动作空间离散化。例如当将战机1的连续动作空间5等分时, a t a_t at 的离散动作空间中的动作个数围为 5 × 5 = 25 5\times 5=25 5×5=25。 -
奖励函数:同之前工作中做的奖励函数一致。
-
状态转移方程: s t + 1 s_{t+1} st+1 与 s t s_t st之间与动作 a t a_t at有关的状态转移方程为:
x t + 1 ( 1 ) = x t ( 1 ) + v 1 Δ t cos ( θ t ( 1 ) + Δ θ t ( 1 ) ) y t + 1 ( 1 ) = y t ( 1 ) + v 1 Δ t sin ( θ t ( 1 ) + Δ θ t ( 1 ) ) θ t + 1 ( 1 ) = θ t ( 1 ) + Δ θ t ( 1 ) x t + 1 ( 2 ) = x t ( 2 ) + v 1 Δ t cos ( θ t ( 2 ) + Δ θ t ( 2 ) ) y t + 1 ( 2 ) = y t ( 2 ) + v 1 Δ t sin ( θ t ( 2 ) + Δ θ t ( 2 ) ) θ t + 1 ( 2 ) = θ t ( 2 ) + Δ θ t ( 2 ) x_{t+1}^{(1)}=x_{t}^{(1)}+v_1\Delta t \cos(\theta_t^{(1)}+\Delta \theta_t^{(1)})\\ y_{t+1}^{(1)}=y_{t}^{(1)}+v_1\Delta t \sin(\theta_t^{(1)}+\Delta \theta_t^{(1)})\\ \theta_{t+1}^{(1)}=\theta_{t}^{(1)} + \Delta \theta_t^{(1)}\\ x_{t+1}^{(2)}=x_{t}^{(2)}+v_1\Delta t \cos(\theta_t^{(2)}+\Delta \theta_t^{(2)})\\ y_{t+1}^{(2)}=y_{t}^{(2)}+v_1\Delta t \sin(\theta_t^{(2)}+\Delta \theta_t^{(2)})\\ \theta_{t+1}^{(2)}=\theta_{t}^{(2)} + \Delta \theta_t^{(2)}\\ xt+1(1)=xt(1)+v1Δtcos(θt(1)+Δθt(1))yt+1(1)=yt(1)+v1Δtsin(θt(1)+Δθt(1))θt+1(1)=θt(1)+Δθt(1)xt+1(2)=xt(2)+v1Δtcos(θt(2)+Δθt(2))yt+1(2)=yt(2)+v1Δtsin(θt(2)+Δθt(2))θt+1(2)=θt(2)+Δθt(2)
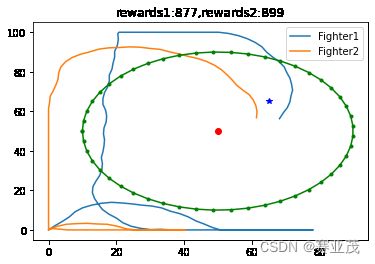
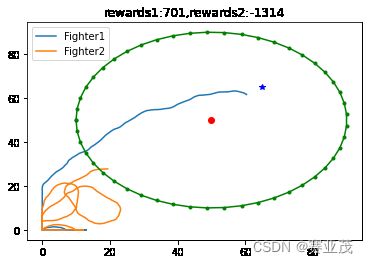
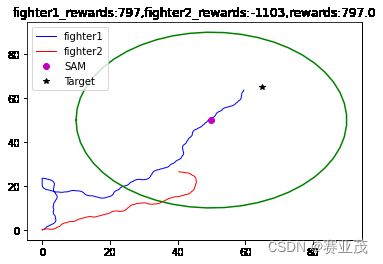
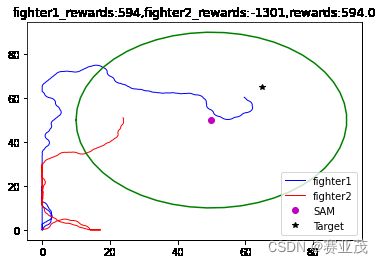
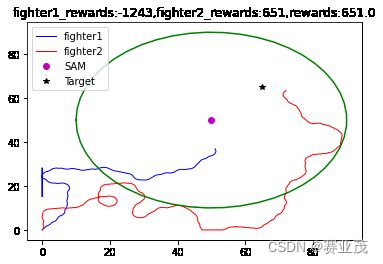
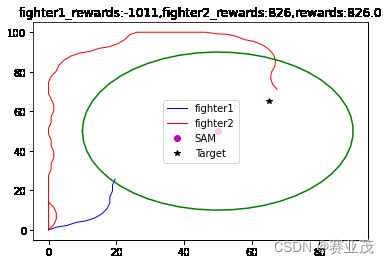
当采取以上参数时,得用离散PPO训练的一组较为优化的轨迹如下:
这个结果就很好的反映了战机的一个迂回穿插袭击Target的轨迹,与人们传统的想法一致。其300次的训练过程如下:
4.代码
当前工作下环境搭建的代码:
import numpy as np
import matplotlib.pyplot as plt
# 下面环境的搭建将是基于全局可观测的
# 下面写战斗机的类
class Fighter(object):
def __init__(self,x0=0.0,y0=0.0,theta0=0,theta_num=6,
fighter_range=20,L_limits=100,theta_range=np.pi/6,
velocity=2175.0/3600,delta_t=10,aim_time=30):
# 下面设置战斗机的基本属性
self.x = x0
self.y = y0
self.theta = theta0
self.fighter_range = fighter_range # 战斗机火力范围
self.L_limits = L_limits # 区域长度限制
self.velocity = velocity # 战斗机速度
self.delta_t = delta_t # 采样时间
self.aim_time = aim_time # 战斗机瞄准时间
self.dead = False # 战斗机的生存状态
self.state = np.array([self.x,self.y,self.theta]) # 战斗机当前状态是包括x0,y0的np数组
# 下面建立离散动作空间的映射表
self.theta_num = theta_num
self.action_space = np.linspace(-theta_range/2,theta_range/2,theta_num)
# 下面开始设置瞄准时间
self.aim_SAM_time = 0.0
self.aim_target_time = 0.0
def reset(self,rand_initial_position=True,theta=np.pi/4):
# 试探性出发假设
if rand_initial_position:
self.x = np.random.random()*self.L_limits
self.y = np.random.random()*self.L_limits
self.theta = np.random.random()*np.pi/2
else:
self.x = 0
self.y = 0
self.theta = theta
self.dead = False
# 下面开始设置瞄准时间
self.aim_SAM_time = 0.0
self.aim_target_time = 0.0
return np.array([self.x,self.y,self.theta])
def step(self,action,SAM,target):
# 动作空间action表示航向{0,1,2,3,4,5,6,..theta_num}
# 这里需要知道SAM的实际位置与target的实际位置
# 下面开始获取当前战斗机位置
# SAM_range:SAM的火力范围
# 下面开始抽取target与SAM的状态
# 下面对动作进行描述
self.theta += self.action_space[int(action)]
self.x += self.velocity*self.delta_t*np.cos(self.theta)
self.y += self.velocity*self.delta_t*np.sin(self.theta)
# # 使战斗机位置在所在区域内,对于角度范围没有限制
if self.x >= self.L_limits:
self.x = self.L_limits
elif self.x <= 0.0:
self.x = 0.0
if self.y >= self.L_limits:
self.y = self.L_limits
elif self.y <= 0.0:
self.y = 0.0
self.state = np.array([self.x,self.y,self.theta])
# 下面开始计算奖励
d_target = np.linalg.norm(np.array([self.x - target.x,self.y - target.y]))
d_SAM = np.linalg.norm(np.array([self.x - SAM.x,self.y - SAM.y]))
# 如果SAM与target在战斗机的火力射程范围外,则无法瞄准,其瞄准时间为0
if d_target >= self.fighter_range:
self.aim_target_time = 0.0
else:
self.aim_target_time += self.delta_t
if d_SAM >= self.fighter_range:
self.aim_SAM_time = 0.0
else:
self.aim_SAM_time += self.delta_t
if d_SAM >= SAM.SAM_range: # Fighter在SAM的火力范围内会计算时间
SAM.aim_Fighter_time = 0.0
else:
SAM.aim_Fighter_time += self.delta_t
# 如果战斗机瞄准时间比较长可以击落target
if self.aim_target_time >= self.aim_time:
target.dead = True
self.aim_target_time = 0.0
return self.state,1000,True # 比较圆满的结果是target被击落
# 如果SAM有弹药且成功击毁Fighter
if (SAM.dead==False) and (d_SAM <= SAM.SAM_range) and (SAM.aim_Fighter_time >= SAM.aim_time):
SAM.dead = True # 此时弹药已经消耗光
SAM.aim_Fighter_time = 0.0
return self.state,-1000,True # 不太圆满的结果是Fighter被击落
# 战斗机同样也击落SAM的可能性
if (SAM.dead==False) and (d_SAM <= self.fighter_range) and (self.aim_SAM_time >= self.aim_time):
SAM.dead = True # SAM 被击毁
self.aim_SAM_time = 0.0
return self.state,50,False
return self.state,-1,False
# 下面开始写SAM的类
class Sam:
def __init__(self,x=50,y=50,SAM_range=30,
L_limits=100,max_aim_time=10):
self.x = x
self.y = y
self.SAM_range = SAM_range
self.L_limits = L_limits
self.aim_time = max_aim_time
self.aim_Fighter_time = 0
self.dead = False
def reset(self):
self.aim_Fighter_time = 0
self.dead = False
# 下面开始写target的类
class Target:
def __init__(self,x=80,y=80,L_limits=100):
self.x = x
self.y = y
self.L_limits = L_limits
self.dead = False
def reset(self):
self.dead = False
# 总环境的搭建
class Fighter2Env(object):
def __init__(self,SAM_x=50,SAM_y=50,Target_x=80,Target_y=80,
Fighter_range=20,SAM_range=30,L_limits=100,
delta_t=10,velocity=2175.0/3600,fighter_action_dim=9,
fighter_aim_time=30,sam_aim_time=10,delta_theta=np.pi/6):
# 构造两个同构战斗机
self.fighter1 = Fighter(x0=0,y0=0,fighter_range=Fighter_range,
L_limits=L_limits,velocity=velocity,
delta_t=delta_t,aim_time=fighter_aim_time)
self.fighter2 = Fighter(x0=0,y0=0,fighter_range=Fighter_range,
L_limits=L_limits,velocity=velocity,
delta_t=delta_t,aim_time=fighter_aim_time)
# 分别构造SAM与Target对象
self.Target = Target(x=Target_x,y=Target_y,L_limits=L_limits)
self.SAM = Sam(x=SAM_x,y=SAM_y,SAM_range=SAM_range,
L_limits=L_limits,max_aim_time=sam_aim_time)
# 战斗机1,2的位置组成战斗机的状态空间
self.observation_space = np.array([[0,L_limits],[0,L_limits],[-delta_theta/2,delta_theta/2],
[0,L_limits],[0,L_limits],[-delta_theta/2,delta_theta/2]])
self.observation_ndim = 6
self.action_space = np.linspace(-delta_theta/2,delta_theta/2,fighter_action_dim)
self.fighter1_action_dim = fighter_action_dim
self.action_dim = int(fighter_action_dim**2) # 9 * 9=81维动作空间,动作空间巨大是一个很大的问题
# 设置2架战斗机的初始位置
fighter1_x0,fighter1_y0,fighter1_theta0 = self.fighter1.reset(theta=np.arctan(self.Target.y/self.Target.x),
rand_initial_position=True)
fighter2_x0,fighter2_y0,fighter2_theta0 = self.fighter2.reset(theta=np.arctan(self.Target.y/self.Target.x),
rand_initial_position=True)
self.state = np.array([fighter1_x0,fighter1_y0,fighter1_theta0,
fighter2_x0,fighter2_y0,fighter2_theta0])
#self.fighter1_theta = np.arctan(Target_y/Target_x)
self.fighter1_done = False # 这里说明两个战斗机都没有被击落
self.fighter1_state = np.array([fighter1_x0,fighter1_y0,fighter1_theta0])
self.fighter1_total_rewards = 0
self.fighter1_x_array = []
self.fighter1_y_array = []
#self.fighter2_theta = np.arctan(Target_y/Target_x)
self.fighter2_done = False # 这里说明两个战斗机都没有被击落
self.fighter2_state = np.array([fighter2_x0,fighter2_y0,fighter2_theta0])
self.fighter2_total_rewards = 0
self.fighter2_x_array = []
self.fighter2_y_array = []
self.done = False
# 下面是动作解码
def action_decode(self,action):
# action:0-80
fighter1_action = int(action)//self.fighter1_action_dim
fighter2_action = int(action)%self.fighter1_action_dim
return fighter1_action,fighter2_action
# 下面是重置函数
def reset(self,rand_initial_position=True):
# 设置2架战斗机的初始位置
self.SAM.reset()
self.Target.reset()
fighter1_x0, fighter1_y0,fighter1_theta0 = self.fighter1.reset(rand_initial_position=rand_initial_position)
fighter2_x0, fighter2_y0,fighter2_theta0 = self.fighter2.reset(rand_initial_position=rand_initial_position)
self.fighter1_state = np.array([fighter1_x0, fighter1_y0,fighter1_theta0])
self.fighter1_theta = np.arctan(self.Target.y/self.Target.x)
self.fighter1_done = False # 这里说明两个战斗机都没有被击落
self.fighter1_total_rewards = 0
self.fighter1_x_array = []
self.fighter1_y_array = []
self.fighter2_state = np.array([fighter2_x0, fighter2_y0,fighter2_theta0])
self.fighter2_theta = np.arctan(self.Target.y/self.Target.x)
self.fighter2_done = False # 这里说明两个战斗机都没有被击落
self.fighter2_total_rewards = 0
self.fighter2_x_array = []
self.fighter2_y_array = []
self.state = np.array([fighter1_x0, fighter1_y0,self.fighter1_theta ,
fighter2_x0, fighter2_y0,self.fighter2_theta])
self.done = False # 回合结束标志
return self.state
# 下面是动作函数
def step(self,action):
# action:0-80
fighter1_action,fighter2_action = self.action_decode(action)
fighter1_total_rewards,fighter2_total_rewards = self.fighter1_total_rewards,self.fighter2_total_rewards
if not self.fighter1_done:
fighter1_state,fighter1_reward,fighter1_done = self.fighter1.step(fighter1_action,self.SAM,self.Target)
self.fighter1_x_array.append(fighter1_state[0])
self.fighter1_y_array.append(fighter1_state[1])
self.fighter1_done = fighter1_done
self.fighter1_state = fighter1_state
self.fighter1_total_rewards += fighter1_reward
if not self.fighter2_done:
fighter2_state,fighter2_reward,fighter2_done = self.fighter2.step(fighter2_action,self.SAM,self.Target)
self.fighter2_x_array.append(fighter2_state[0])
self.fighter2_y_array.append(fighter2_state[1])
self.fighter2_done = fighter2_done
self.fighter2_state = fighter2_state
self.fighter2_total_rewards += fighter2_reward
self.state = np.array([self.fighter1_state[0],self.fighter1_state[1],self.fighter1_state[2],
self.fighter2_state[0],self.fighter2_state[1],self.fighter2_state[2]])
# 下面开始设置奖励函数
## 如果两个累计奖励都不变化
if (self.fighter1_total_rewards != fighter1_total_rewards) and (self.fighter2_total_rewards != fighter2_total_rewards):
reward = max(self.fighter1_total_rewards - fighter1_total_rewards,self.fighter2_total_rewards - fighter2_total_rewards)
else:
reward = (self.fighter1_total_rewards + self.fighter2_total_rewards) - (fighter1_total_rewards + fighter2_total_rewards)
# 当二者都True结束时真的结束
if self.fighter1_done and self.fighter2_done: # 这里可以用故障树分析!!!
self.done = True
else:
self.done = False
return self.state,reward,self.done
# 下面是根据画图
def render(self):
x1, y1 = [], []
for theta in np.linspace(-np.pi, np.pi):
x1.append(self.SAM.x + self.SAM.SAM_range * np.cos(theta))
y1.append(self.SAM.y + self.SAM.SAM_range * np.sin(theta))
plt.plot(self.fighter1_x_array,self.fighter1_y_array)
plt.plot(self.fighter2_x_array,self.fighter2_y_array)
plt.plot(x1,y1,'g.-')
plt.plot(self.SAM.x,self.SAM.y,'ro')
plt.plot(self.Target.x,self.Target.y,'b*')
plt.title("rewards1:{},rewards2:{}".format(self.fighter1_total_rewards,self.fighter2_total_rewards))
plt.legend(['Fighter1', 'Fighter2'])
plt.show()
if __name__ == "__main__":
env = Fighter2Env(delta_t=1, L_limits=100, Fighter_range=10,
SAM_range=40, SAM_x=50, SAM_y=50, Target_x=65,
Target_y=65, sam_aim_time=5, fighter_aim_time=10,
fighter_action_dim=5)
env.reset(rand_initial_position=False)
while True:
action = np.random.randint(low=0, high=env.action_dim)
env.step(action)
if env.done:
break
env.render()
离散PPO代码这部分的基础知识可以参考以前的博文:基于强化学习的多战机同SEAD联合作战空战辅助决策
5.采用连续ppo算法求解
用以下代码进行训练:
# 声明环境
args = args_param(max_episode_steps=2000,batch_size=2048,max_train_steps=3000,K_epochs=10)
# 声明参数
env = Fighter_ContinuousEnv(delta_t=1, L_limits=100, Fighter_range=10,
SAM_range=40, SAM_x=50, SAM_y=50, Target_x=65,
Target_y=65, sam_aim_time=5, fighter_aim_time=10)
agent = train_network(args,env)
用以下代码进行测试:
s = env.reset(rand_initial_position=False)
x1,y1,theta1,x2,y2,theta2 = [s[0]],[s[1]],[s[2]],[s[3]],[s[4]],[s[5]]
rewards = 0.0
while True:
a,_ = agent.choose_action(s)
s_,r,done = env.step(a)
s = s_
rewards += r
x1.append(s[0])
y1.append(s[1])
x2.append(s[3])
y2.append(s[4])
if done:
print("当前奖励为:{}".format(rewards))
break
用以下代码进行画图:
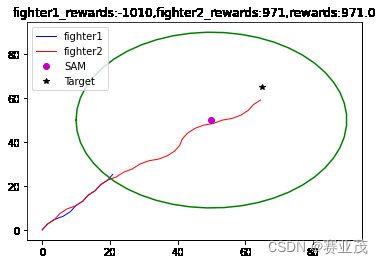
plt.plot(x1,y1,'b-',linewidth=1)
plt.plot(x2,y2,'r-',linewidth=1)
circle_x,circle_y = [],[]
for theta in np.linspace(-np.pi,np.pi,50):
x = env.SAM.x + env.SAM.SAM_range*np.cos(theta)
y = env.SAM.y + env.SAM.SAM_range*np.sin(theta)
circle_x.append(x)
circle_y.append(y)
plt.plot(env.SAM.x,env.SAM.y,'mo')
plt.plot(env.Target.x,env.Target.y,'k*')
plt.plot(circle_x,circle_y,'g-')
plt.legend(['fighter1','fighter2','SAM','Target'])
plt.title("fighter1_rewards:{},fighter2_rewards:{},rewards:{}".format(env.fighter1_total_rewards,env.fighter2_total_rewards,rewards))
连续ppo算法的代码如下:
import matplotlib.pyplot as plt
import numpy as np
from normalization import Normalization, RewardScaling
from replaybuffer import ReplayBuffer
from ppo_continuous import PPO_continuous
from fighter2_continuous import Fighter_ContinuousEnv
# 先定义一个参数类,用来储存超参数
class args_param(object):
def __init__(self,max_train_steps=int(3e6),
evaluate_freq=5e3,
save_freq=20,
policy_dist="Gaussian",
batch_size=2048,
mini_batch_size=64,
hidden_width=64,
lr_a=3e-4,
lr_c=3e-4,
gamma=0.99,
lamda=0.95,
epsilon=0.2,
K_epochs=10,
max_episode_steps = 1000,
use_adv_norm=True,
use_state_norm=True,
use_reward_norm=False,
use_reward_scaling=True,
entropy_coef=0.01,
use_lr_decay=True,
use_grad_clip=True,
use_orthogonal_init=True,
set_adam_eps=True,
use_tanh=True):
self.max_train_steps = max_train_steps
self.evaluate_freq = evaluate_freq
self.save_freq = save_freq
self.policy_dist = policy_dist
self.batch_size = batch_size
self.mini_batch_size = mini_batch_size
self.hidden_width = hidden_width
self.lr_a = lr_a
self.lr_c = lr_c
self.gamma = gamma
self.lamda = lamda
self.epsilon = epsilon
self.K_epochs = K_epochs
self.use_adv_norm = use_adv_norm
self.use_state_norm = use_state_norm
self.use_reward_norm = use_reward_norm
self.use_reward_scaling = use_reward_scaling
self.entropy_coef = entropy_coef
self.use_lr_decay = use_lr_decay
self.use_grad_clip = use_grad_clip
self.use_orthogonal_init = use_orthogonal_init
self.set_adam_eps = set_adam_eps
self.use_tanh = use_tanh
self.max_episode_steps = max_episode_steps
def print_information(self):
print("Maximum number of training steps:",self.max_train_steps)
print("Evaluate the policy every 'evaluate_freq' steps:",self.evaluate_freq)
print("Save frequency:",self.save_freq)
print("Beta or Gaussian:",self.policy_dist)
print("Batch size:",self.batch_size)
print("Minibatch size:",self.mini_batch_size)
print("The number of neurons in hidden layers of the neural network:",self.hidden_width)
print("Learning rate of actor:",self.lr_a)
print("Learning rate of critic:",self.lr_c)
print("Discount factor:",self.gamma)
print("GAE parameter:",self.lamda)
print("PPO clip parameter:",self.epsilon)
print("PPO parameter:",self.K_epochs)
print("Trick 1:advantage normalization:",self.use_adv_norm)
print("Trick 2:state normalization:",self.use_state_norm)
print("Trick 3:reward normalization:",self.use_reward_norm)
print("Trick 4:reward scaling:",self.use_reward_scaling)
print("Trick 5: policy entropy:",self.entropy_coef)
print("Trick 6:learning rate Decay:",self.use_lr_decay)
print("Trick 7: Gradient clip:",self.use_grad_clip)
print("Trick 8: orthogonal initialization:",self.use_orthogonal_init)
print("Trick 9: set Adam epsilon=1e-5:",self.set_adam_eps)
print("Trick 10: tanh activation function:",self.use_tanh)
# 下面函数用来训练网络
def train_network(args,env,show_picture=True):
epsiode_rewards = []
epsiode_mean_rewards = []
# 下面将导入env环境参数
args.state_dim = env.observation_space.shape[0]
args.action_dim = env.action_space.shape[0]
args.max_action = float(env.action_space[0][1])
# 下面将定义一个缓冲区
replay_buffer = ReplayBuffer(args)
# 下面将定义一个PPO智能体类
agent = PPO_continuous(args)
# 下面将采用Trick 2技巧标准化
state_norm = Normalization(shape=args.state_dim)
if args.use_reward_norm:
reward_norm = Normalization(shape=1)
elif args.use_reward_scaling: # Trick 4:reward scaling
reward_scaling = RewardScaling(shape=1, gamma=args.gamma)
# 下面开始进行训练过程
for epsiode in range(args.max_train_steps):
# 每个回合首先对值进行初始化
epsiode_reward = 0.0
done = False
epsiode_count = 0
# 再赋予一个新的初始状态
s = env.reset()
# 对状态进行标准化操作
if args.use_state_norm:
s = state_norm(s)
if args.use_reward_scaling:
reward_scaling.reset()
# 设置一个死循环,后面若跳出便在死循环中跳出
while True:
# 每执行一个回合,count次数加1
epsiode_count += 1
a,a_logprob = agent.choose_action(s)
# 根据参数的不同选择输出是高斯分布/Beta分布调整
if args.policy_dist == "Beta":
action = 2*(a-0.5)*args.max_action
else:
action = a
# 下面是执行环境交互操作
s_,r,done = env.step(action) ## !!! 这里的环境是自己搭建的,输出每个人都不一样
s_ = s_.T[0] ## !!! 这一部起始没必要,由于我的环境有问题所以加的这一步
epsiode_reward += r
# 下面考虑状态标准化的情况
if args.use_state_norm:
s_ = state_norm(s_)
# 下面考虑奖励标准化的可能性
if args.use_reward_norm:
r = reward_norm(r)
elif args.use_reward_scaling:
r = reward_scaling(r)
# 下面考虑回合的最大运行次数(只要回合结束或者超过最大回合运行次数)
if done or epsiode_count >= args.max_episode_steps:
dw = True
else:
dw = False
# 将经验存入replayBuffer中
replay_buffer.store(s,action,a_logprob,r,s_,dw,done)
# 重新赋值状态
s = s_
# 当replaybuffer尺寸到达batchsize便会开始训练
if replay_buffer.count == args.batch_size:
agent.update(replay_buffer,epsiode)
replay_buffer.count = 0
# 如果回合结束便退出
if done:
epsiode_rewards.append(epsiode_reward)
epsiode_mean_rewards.append(np.mean(epsiode_rewards))
print("第{}次训练的奖励为{:.2f},平均奖励为{:.2f}".format(epsiode,
epsiode_reward, epsiode_mean_rewards[-1]))
break
# 如果需要画图的话
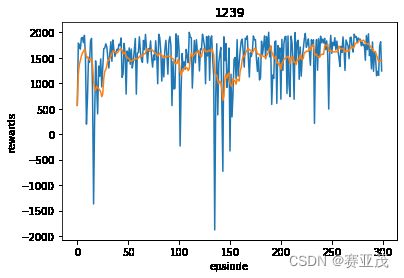
if show_picture:
plt.plot(epsiode_rewards)
plt.plot(epsiode_mean_rewards)
plt.xlabel("epsiodes")
plt.ylabel("rewards")
plt.title("Continuous PPO With Optimization")
plt.legend(["rewards","mean_rewards"])
plt.show()
return agent