Numpy笔记
Numpy笔记
-
- 3.1 Numpy优势
-
- 3.1.2 ndarray介绍
- 3.1.3 ndarray与Python原生list运算效率对比
- 3.1.4 ndarray的优势
- 3.2 认识N维数组-ndarray属性
-
- 3.2.1 ndarray的属性
- 3.2.2 ndarray的形状
- 3.3 基本操作
-
- 3.3.1 生成数组的方法
- 3.3.2 数组的索引、切片
- 3.3.3 形状修改
- 3.3.4 类型修改
- 3.3.5 数组的去重
- 3.4 ndarray运算
-
- (一)逻辑运算
- (二)统计运算
- (三)数组间运算
-
- 3.5.2 数组与数的运算
- 3.5.3 数组与数组的运算
- 3.5.4 广播机制
- 3.5.5 矩阵运算
- 3.6 合并、分割
- 3.7 IO操作与数据处理
-
- 3.7.1 Numpy读取
- 3.7.2 如何处理缺失值
Numpy 高效的运算工具
ndarray运算
逻辑运算
统计运算
数组间运算
合并、分割、IO操作、数据处理
![]()
3.1 Numpy优势
3.1.1 Numpy介绍 - 数值计算库
num - numerical 数值化的
py - python
ndarray
n - 任意个
d - dimension 维度
array - 数组
3.1.2 ndarray介绍
NumPy提供了一个N维数组类型ndarray,它描述了**相同类型的"items"**的集合
#优势
3.1.3 ndarray与Python原生list运算效率对比
import numpy as np
import time
import random
score=np.array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])
#生成一个数组
python_list=[]
for i in range(10000000):
python_list.append(random.random())
ndarray_list=np.array(python_list)
#python的list
t1=time.time()
a=sum(python_list)
t2=time.time()
print(t2-t1)
t3=time.time()
b=np.sum(ndarray_list)
t4=time.time()
print(t4-t3)
0.0708153247833252
0.014972209930419922
3.1.4 ndarray的优势
1)存储风格
ndarray - 相同类型 - 通用性不强
list - 不同类型 - 通用性很强
2)并行化运算
ndarray支持向量化运算
3)底层语言
C语言,解除了GIL
3.2 认识N维数组-ndarray属性
3.2.1 ndarray的属性
| 属性名称 | 属性解释 |
|---|---|
| ndarray.shape | 数组维度的元组 |
| ndarray.ndim | 数组维数 |
| ndarray.size | 数组中的元素数量 |
| ndarray.itemsize | 一个数组元素的长度(字节) |
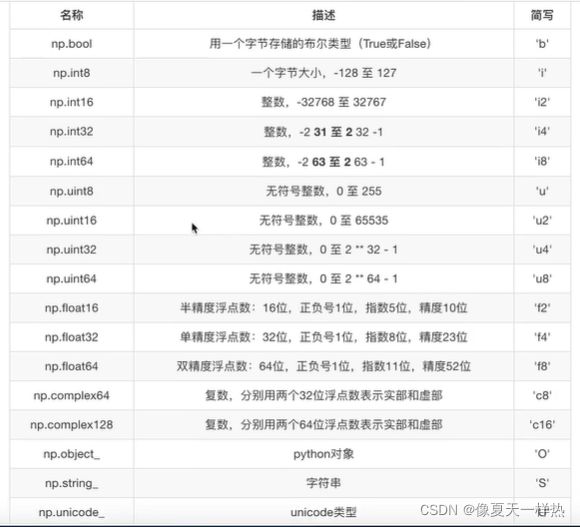
| ndarray.dtype | 数组元素的类型( 在创建ndarray的时候,如果没有指定类型默认 整数 int64 浮点数 float64) |
import numpy as np
score=np.array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])
print(f"形状:{score.shape}")
print(f"维度:{score.ndim}")
print(f"元素数量:{score.size}")
print(f"类型:{score.dtype}")
print(f"一个语素的大小:{score.itemsize}")
# 创建数组的时候指定类型
np.array([1.1, 2.2, 3.3], dtype="float32")
np.array([1.1, 2.2, 3.3], dtype=np.float32)
形状:(8, 5)
维度:2
元素数量:40
类型:int32
一个语素的大小:4
3.2.2 ndarray的形状
import numpy as np
a=np.array( [1, 2, 3, 4] ) #一维(1,)
b=np.array([[1, 2, 3, 4], #二维(3,4)
[1, 2, 3, 4],
[1, 2, 3, 4]])
c=np.array([[[1, 2, 3, 4], #三维(3,3,4)
[1, 2, 3, 4],
[1, 2, 3, 4]],
[[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]],
[[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]]])
print(f"a形状{a.shape}")
print(f"b形状{b.shape}")
print(f"c形状{c.shape}")
a形状(4,)
b形状(3, 4)
c形状(3, 3, 4)
3.3 基本操作
adarray.方法()
np.函数名()
np.array()
3.3.1 生成数组的方法
1)生成0和1
np.zeros(shape)
np.zeros((3,4))
np.zeros(shape=(3,4),dtype="float64")
np.ones(shape)
np.ones(shape=(3,4),dtype="float64")
np.ones(shape=[2, 3], dtype=np.int32)
2)从现有数组中生成
score=np.array([[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])
#深拷贝--重新创建了数组
#浅拷贝--没有重新创建数组,只进行了索引
data1 = np.array(score) # 深拷贝
data2 = np.asarray(score) # 浅拷贝
data3 = np.copy(score) # 深拷贝
3)生成固定范围的数组
np.linspace(0, 10, 100)# 0-10 等距离生成100个数
[0, 10] 0闭合,10闭合,等距离
例:
np.linspace(0,10,5)
--》array([ 0. , 2.5, 5. , 7.5, 10. ])
np.arange(a, b, c) #a-b步长c
[a, b) a闭合,b开,c是步长
例:
np.arange(0,10,2)
--》array([0, 2, 4, 6, 8])
4)生成随机数组
分布状况 - 直方图
1)均匀分布
每组的可能性相等
# 生成均匀分布的一组数[low,high)
#从low-high随机采样,左闭右开,size数据量
data1 = np.random.uniform(low=-1, high=1, size=1000000)
from matplotlib import pyplot as plt
plt.figure(figsize=(20,8),dpi=80)
plt.hist(data1,10000)
plt.show()
2)正态分布
μ均值 σ 标准差 幅度、波动程度、集中程度、稳定性、离散程度

方差:

标准差:
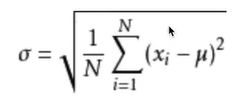
# 生成正态分布的一组数,loc:均值(对称轴);scale:标准差
data2 = np.random.normal(loc=1.75, scale=0.1, size=1000000)
from matplotlib import pyplot as plt
plt.figure(figsize=(20,8),dpi=80)
plt.hist(data2,10000)
plt.show()
3.3.2 数组的索引、切片
#8只股票两周交易日数据(10天)
stock_change=np.random.normal(loc=0,scale=1,size=(8, 10))
#获取第一支股票前三个交易日的涨跌数据
stock_change[0,1] #二维度 数据取值--取第一行第二个数据
stock_change[0,:3] #列 进行切片---取前三个
三维:
a1=np.random.uniform(low=1,high=10,size=(3,2,3))
a1.shape
a1[1,1,1]
输出:
array([[[8.70049876, 9.93619126, 7.73370012],
[1.09430792, 4.38404288, 6.98579176]],
[[1.40222372, 3.63577369, 9.16166421],
[1.4860602 , 4.08693516, 8.07739258]],
[[3.92915707, 1.67903719, 4.88658457],
[7.87125165, 2.17489838, 3.19750204]]])
4.086935164553364
3.3.3 形状修改
(1) ndarray.reshape(shape) 返回新的ndarray,原始数据没有改变
a1=np.random.uniform(low=1,high=10,size=(3,4))
a1
a1.reshape((4,3))
#原始数据a1
array([[5.60500373, 8.72161176, 7.86130914, 7.50406727],
[8.17364736, 6.47552821, 5.1970167 , 7.26511887],
[9.14093054, 5.64902841, 6.90000473, 8.99393082]])
#a1 reshape()后
array([[5.60500373, 8.72161176, 7.86130914],
[7.50406727, 8.17364736, 6.47552821],
[5.1970167 , 7.26511887, 9.14093054],
[5.64902841, 6.90000473, 8.99393082]])
(2) ndarray.resize(shape) 没有返回值,对原始的ndarray进行了修改
a1.resize((4,3))
#a1 resize后
array([[5.60500373, 8.72161176, 7.86130914],
[7.50406727, 8.17364736, 6.47552821],
[5.1970167 , 7.26511887, 9.14093054],
[5.64902841, 6.90000473, 8.99393082]])
(3)ndarray.T 转置 行变成列,列变成行----转置
a1.T
#a1 转置后 行变成列,列变成行
array([[4.17448716, 9.90722989, 9.96374063],
[9.53599125, 2.47426122, 6.82785891],
[3.33629652, 1.465962 , 9.25083382],
[7.31726594, 7.12043049, 9.37375175]])
3.3.4 类型修改
ndarray.astype(type)
stock_change.astype("int64")
array([[ 0, 0, 0, 0, 0, 0, -1, 0, 2, -1],
[ 0, 0, 1, 0, 1, 0, 2, 0, 0, 1],
[ 0, 0, 1, 0, 0, 0, 0, 1, 0, 0],
[ 2, 0, 0, 0, 0, -1, 0, 0, 0, 0],
[ 0, 0, 1, 0, 0, -1, 0, 0, 0, 0],
[-2, 0, 0, 0, -1, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 0, 0, 2, -1, 0, 0],
[-1, 0, 0, 0, 0, 0, -1, 0, 0, 0]], dtype=int64)
ndarray序列化到本地
ndarray.tostring()
stock_change.tostring() # ndarray序列化到本地
3.3.5 数组的去重
b=np.array([[1, 2, 3, 4], #二维(3,4)
[1, 2, 3, 4],
[1, 2, 3, 4]])
np.unique(b)
-->array([1, 2, 3, 4])
使用set数据必须是一维的:所以先展平
set(temp.flatten())
-->{1, 2, 3, 4}
3.4 ndarray运算
(一)逻辑运算
布尔索引
stock_change=np.random.normal(loc=0,scale=1,size=(3, 4)) #两周交易日10天
stock_change
-->array([[ 0.03168576, -0.84114358, -0.15573287, -0.757188 ],
[-0.67288526, 1.11056923, -0.35185445, 0.20066526],
[ 0.35186827, -0.7508142 , 0.50245255, 1.8511653 ]])
# 逻辑判断, 如果涨跌幅大于0.5就标记为True 否则为False
stock_change > 0.5
-->array([[False, False, False, False],
[False, True, False, False],
[False, False, True, True]])
stock_change[stock_change > 0.5] = 2
stock_change
-->array([[ 2. , -0.42716664, 2. , -2.24569804],
[ 0.27978041, -0.03538432, -0.21644275, -0.19097601],
[ 2. , 2. , -1.27567962, 2. ]])
通用判断函数
np.all(布尔值)
只要有一个False就返回False,只有全是True才返回True
np.any(布尔值)
只要有一个True就返回True,只有全是False才返回False
stock_change>0
-->array([[False, True, False, False],
[ True, True, True, True],
[ True, True, True, True]])
np.all(stock_change>0)
-->False
np.any(stock_change)
-->True
三元运算符
np.where(三元运算符)
np.where(布尔值, True的位置的值, False的位置的值)
stock_change=np.random.normal(loc=0,scale=1,size=(3, 4))
stock_change
-->array([[-1.00412336, 1.51447151, -0.02444968, -1.2600538 ],
[ 1.09021281, 0.91958616, 0.18345248, 0.28801944],
[ 0.38189105, 0.11208632, 0.0432234 , 1.29729351]])
np.where(stock_change>0,1,0)
array([[0, 1, 0, 0],
[1, 1, 1, 1],
[1, 1, 1, 1]])
# 大于0.5且小于1
#np.logical_and(temp > 0.5, temp < 1) 使用逻辑运算符函数logical_and()
np.where(np.logical_and(stock_change > 0.5, stock_change < 1), 1, 0)
# 大于0.5或小于-0.5
np.where(np.logical_or(temp > 0.5, temp < -0.5), 11, 3)
(二)统计运算
统计指标函数
min, max, mean, median, var(方差), std(标准差)—一 一对应相应的函数
两种使用方式:
- np.函数名
- ndarray.方法名
#返回array所有数据的最大值
#1.
np.max(stock_change)
#2.
stock_change.max()
按行、按列求最大值 0-列 ,1-行(维度下标)//还是试一下吧
stock_change=np.random.normal(loc=0,scale=1,size=(3, 4))
stock_change
-->array([[ 0.88128531, -0.43458763, 1.10651898, 0.04986138],
[ 1.90579788, -0.65613119, -0.1087075 , -0.12294807],
[ 0.1417611 , 1.64306952, -0.70325562, -0.52802373]])
np.max(stock_change,axis=0)
stock_change.max(axis=0)
-->array([1.90579788, 1.64306952, 1.10651898, 0.04986138])
np.max(stock_change,axis=1)
stock_change.max(axis=1)
-->array([1.10651898, 1.90579788, 1.64306952])
返回最大值、最小值所在位置
np.argmax(temp, axis=)
np.argmin(temp, axis=)
np.argmax(temp, axis=-1) #按行求最大值位置
-->array([2, 0, 1], dtype=int64)
(三)数组间运算
3.5.2 数组与数的运算
arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr * 10
-->array([[10, 20, 30, 20, 10, 40],
[50, 60, 10, 20, 30, 10]])
3.5.3 数组与数组的运算
arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr
arr2=np.array([[1, 2, 3,4], [5, 6, 1, 2]])
arr2
arr+arr2
-->ValueError: operands could not be broadcast together with shapes (2,6) (2,4)
could not be broadcast
3.5.4 广播机制
执行broadcast的前提在于,两个nadarray执行的是element-wise的运算,Broadcast机制的功能是为了方便不同形状的ndarray(numpy库的核心数据结构)进行数学运算。
当操作两个数组时,numpy会逐个比较它们的shape(构成的元组tuple),只有在下述情况下,两个数组才能够进行数组与数组的运算。1.维度相等
2. shape(其中相对应的一个地方为1)
arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr
-->array([[1, 2, 3, 2, 1, 4],
[5, 6, 1, 2, 3, 1]])
arr.shape
-->(2, 6)
arr2=np.array([[1], [5]])
arr2
-->array([[1],
[5]])
arr2.shape
-->(2, 1)
arr+arr2
-->array([[ 2, 3, 4, 3, 2, 5],
[10, 11, 6, 7, 8, 6]])
(arr+arr2).shape
-->(2, 6)
3.5.5 矩阵运算
1 什么是矩阵
矩阵matrix == 二维数组
矩阵 & 二维数组
矩阵乘法运算规则:

两种方法存储矩阵
- ndarray 二维数组
score_ndarray =np.array([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
score_ndarray.shape
-->(8, 2)
score_ndarray
-->array([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
数组存储的矩阵 的矩阵乘法(三种方式):
1. np.matmul
2. np.dot
3. data@data1
score_ndarray =np.array([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
weights=np.array([[0.3],
[0.7]])
#矩阵乘法的三种方式:
np.matmul(score_ndarray,weights)
np.dot(score_ndarray,weights)
score_ndarray@weights
-->
array([[86.3],
[91.3],
[92.8],
[91. ],
[83.7],
[76.3],
[92.6],
[85.3]])
- matrix数据结构
score_matrix=np.mat([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
score_matrix.shape
-->(8, 2)
score_matrix
-->matrix([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
矩阵乘法运算
形状
(m, n) * (n, l) = (m, l)
运算规则
A (2, 3) B(3, 2)
A * B = (2, 2)
matrix存储的矩阵乘法:
score_matrix=np.mat([[80, 89],
[78, 97],
[90, 94],
[91, 91],
[76, 87],
[70, 79],
[94, 92],
[86, 85]])
we**加粗样式**ights_matrix=np.mat([[0.3],
[0.7]])
score_matrix*weights_matrix
-->
matrix([[86.3],
[91.3],
[92.8],
[91. ],
[83.7],
[76.3],
[92.6],
[85.3]])
3.6 合并、分割
a=np.array((1,2,3))
b=np.array((4,5,6))
np.hstack((a,b))
>>>array([1, 2, 3, 4, 5, 6]
a=np.array([
[1],
[2],
[3]
])
b=np.array([
[2],
[3],
[4]
])
np.hstack((a,b))
>>>array([[1, 2],
[2, 3],
[3, 4]])
竖直拼接:
a=np.array((1,2,3))
b=np.array((4,5,6)
np.vstack((a,b)
>>>array([[1, 2, 3],
[4, 5, 6]])
a=np.array([
[1],
[2],
[3]
])
b=np.array([
[2],
[3],
[4]
])
np.vstack((a,b))
>>>array([[1],
[2],
[3],
[2],
[3],
[4]])
concatenate拼接:
#竖直拼接
a=np.array([
[1,2],
[3,4]
])
b=np.array([[5,6]])
np.concatenate((a,b),axis=0)
>>>array([[1, 2],
[3, 4],
[5, 6]]
#水平拼接
a=np.array([
[1,2],
[3,4]
])
b=np.array([[5,6]])
np.concatenate((a,b.T),axis=1)
array([[1, 2, 5],
[3, 4, 6]]
(2)分割
x=np.arange(9.0)
x
np.split(x,3)
>>>[array([0., 1., 2.]), array([3., 4., 5.]), array([6., 7., 8.])
x=np.arange(9.0
>>>array([0., 1., 2., 3., 4., 5., 6., 7., 8.]
np.split(x,[3,5,6])
>>>[array([0., 1., 2.]), array([3., 4.]), array([5.]), array([6., 7., 8.])
3.7 IO操作与数据处理
3.7.1 Numpy读取
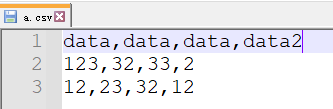
np.genfromtxt("a.csv", delimiter=",") # 会有问题,读不出字符串
## 读取不出字符串
>>>array([[ nan, nan, nan, nan],
[123., 32., 33., 2.],
[ 12., 23., 32., 12.]])
3.7.2 如何处理缺失值
两种思路:
直接删除含有缺失值的样本
替换/插补
按列求平均,用平均值进行填补
缺失值类型:
data=np.genfromtxt("a.csv", delimiter=",") # 会有问题,读不出字符串
type(data[0,1])
>>> numpy.float64