[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN
文章目录
- 1. 前言
- 2. Overview of Sparsity in Deep Learning
-
- 2.1 Generalization
- 2.2 performance and model storage
- 2.3 what can be sparsified?
- 2.4 when to sparsify
- 2.5 Input Feature Selection
- 2.6 Ensembles
- 3. Pruning Criteria - How to Select Elements to Remove
-
- 3.1 Structured vs. unstructured element removal
- 3.2 Data-free selection
- 3.3 Data-driven selection based on sensitivity
- 3.4 Data-driven selection based on 1st order Taylor expansion of the training loss function
- 3.5 Selection based on 2nd order Taylor expansion of the training loss function
- 3.6 Selection based on regularization of the loss during training
- 3.7 Variational selection schemes
- 3.8 Other selection schemes
- 3.9 Parameter budgets between different layers
- 4. Dynamic Pruning: Network regrowth during training
-
- 4.1 Random or uniform regrowth
- 4.2 Gradient information based
- 4.3 Locality-based and greedy regrowth
- 5. Ephemeral Sparsification Approaches
-
- 5.1 Sparsifying neuron activations
- 5.2 Dropout techniques for training
- 5.3 Gradients
-
- 5.3.1 Magnitude-based gradient sparsification
- 5.3.2 Variance-based gradient sparsification
- 5.3.3 Other methods for gradient sparsification
- 5.3.4 Convergence of sparsified gradient methods
- 5.3.5 Runtime support for sparse gradient summation
- 5.3.6 Gradient sparsification for better accuracy
- 5.4 Errors and optimizer state
- 5.5 Dynamic networks with conditional computation
- 6. Sparsifying Particular Neural Network Architectures
-
- 6.1 Sparsifying convolutional neural networks
-
- 6.1.1 CNN architecture evolution
- 6.1.2 CNN sparsification techniques
- 6.2 Sparsifying transformer networks
-
- 6.2.1 Structured sparsification
- 6.2.2 Unstructured sparsification
- 6.2.3 Sparse attention
- 7. Speeding up Sparse Models
- 8. Discussion
-
- 8.1 Relation to Biological Brains
- 8.2 Permutation Groups and Information Loss
- 8.3 Sparse subnetworks for training and lottery tickets
-
- 8.3.1 Pruning is all you need - networks without weight training
- 8.3.2 Lottery tickets in large networks
- 9. Challenges and Open Question
- 典型相关工作整理
-
- layer-wise unstructured sparsity
1. 前言
论文地址:https://arxiv.org/abs/2102.00554
2. Overview of Sparsity in Deep Learning
2.1 Generalization
sparse model的精确度和计算性能随稀疏程度的变化,分别如下图的绿\红所示。
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第1张图片](http://img.e-com-net.com/image/info8/fece2bd26cfe43db98228951f6ab9532.jpg)
2.2 performance and model storage
实现模型稀疏化需要存储的数据格式,如下面的bitmap就是存储一个模型参数个数大小的0/1矩阵,作为mask。

2.3 what can be sparsified?
- model sparsity:模型的稀疏模式不会随着单个样本而改变
- weights:细粒度,优点:精度高;缺点:非结构化稀疏,硬件不友好
- neurons&neuron-like:粗粒度,优点:稀疏化的模型可以重组成一个新的稠密模型,硬件友好
- ephemeral sparsification:模型的稀疏模式视输入样本而定
2.4 when to sparsify
- Sparsify after training:稠密模型收敛之后,裁剪,微调到第二次收敛
- 优点:性能好(有工作表明,收敛之前的裁剪会影响最终性能)
- 缺点:训练效率低
- Sparsify during training:边训练边裁剪
- 优点:先前裁剪的错误可能被改善; 避免了layer collapse问题
- 缺点:收敛速度慢;受超参影响大;
- 关键:以怎样的频率,每次裁剪多少元素,相关工作有:
- Prechelt:使用泛化性作为损失,来调整裁剪率
- Iterative hard thresholding:(dense)->sparse->dense
- 一些发现:
- early structure adaptation:the importance of elements is determined relatively early on in training
- a large learning rate in earlier iterations helps the model to memorize easy to fit patterns that are later refined
- sparsity may naturally emerge from the optimization process
- early structure adaptation:the importance of elements is determined relatively early on in training
- Sparse training:先进行稀疏初始化,然后进行稀疏训练,期间可能进一步grow\prune
- Dynamic sparsity during training:
- SET:magnitude pruning、random regrowth、balanced parameter budget
- NeST:a random seed architecture、a growth phase、a pruning phase
- RigL:weights for training fixed、magnitudes、gradients.
- Fixed sparsity during training:
- 特点:
- Liu:one can train structured sparse models from scratch without pruning if the architecture and hyperparameters are chosen well and that such sparse training may improve performance(structured pruning可能更有效)
- Frankle\Su:
-the most significant feature of those methods is the sparsity ratio per layer. Specifically, they demonstrate that a dataindependent random sparsity structure with the right density ratio at each layer achieves competitive, sometimes even better performance than more complex methods such as SNIP and GraSP- those methods generally achieve accuracies below the baseline of magnitude pruning after training.
- data-driven:
- SNIP:identifies unstructured sparsity in the network in a data-driven way before training using importance score evaluation(缺点:They observe that SNIP can hinder gradient flow and performs worse than random pruning at high sparsity (de Jorge et al., 2021), because it considers the gradient for each weight in isolation)(一阶导)
- GraSP:gradient flows and only prunes weights that decrease the gradient norm(二阶导)
- SNIP-it&SNAP-it:some elements that may be of medium importance initially, gain importance with increased pruning, roughly following the gradient flow argument. They iteratively removing elements according to importance score evaluation
- data-free:
- signal propagation:better signal propagation leads to better properties during training
- ?ensure a minimal flow to overcome layer collapse
- 特点:
- Dynamic sparsity during training:
- Ephemeral sparsity during training
- SWAT: a simple top-k selection to remove small weights during the forward pass and both small weights and activations during the backward pass(从rigl的代码来看,被裁剪掉的参数依然会被计算梯度,而这里的方法,可能和NA-MNMT一样?同时操控前向计算和反向传播?)
- Sparsity for transfer learning and fine tuning
- first order(gradient-based)
- magnitude-based
- Diff pruning:defining task-specific model parameters as difference over the pretrained parameters,they sparsify the task-specific differences wtask by up to xxx
- General Sparse Deep Learning Schedules:
- 流程如下图所示
- (5)的意义:裁剪过后的finetune能够把裁剪带来的loss给补回来;裁剪完成后的finetune也能够提升性能
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第5张图片](http://img.e-com-net.com/image/info8/1b8caef1349a4389abc98a574e795353.jpg)
- (4)-(5)的频率:There have not been many structured studies on how to tune this new hyperparameter but it seems related to the choice of minibatch size and ideas such as gradient noise (McCandlish et al., 2018) may be a good starting point. Raihan and Aamodt (2020) show that a higher update frequency is better for training based on ephemeral weight and activation sparsity. Many works also consider tempering hyperparameters on a specific schedule during training (e.g., sparsification probability, Guo et al., 2016), similarly to other hyperparameters (e.g., learning rate schedules).
2.5 Input Feature Selection
- Engelbrecht:each output’s sensitivity with respect to each input for each example
- Castellano and Fanelli:the contribution of an input neuron
- QuickSelection:uses a sparse denoising autoencoder with a single hidden layer to quickly select salient input features in an unsupervised manner
2.6 Ensembles
- train an ensemble of multiple smaller models and average
- combine their outputs to make a final selection
3. Pruning Criteria - How to Select Elements to Remove
3.1 Structured vs. unstructured element removal
- fine-grained unstructured sparsity:Both add significant cost to processing and storing sparse deep neural networks.
- Structured sparsity:Structured sparsity promises highest performance and lowest storage overheads but it may lead to worse models because it may limit the degrees of freedom in the sparsification process
- the removal of whole neurons in a fullyconnected layer
- convolutional filters
- transformer heads
- Strided sparsity
3.2 Data-free selection
- 不同方法:
- based on magnitude
- 特点:
- It is often used together with re-training the sparsified network and training schedules where the sparsity is gradually increased over time
- (unstructured)It can be applied to either individual weights;(structured) or arbitrary groups of weights using ∑ |Wi| for structured pruning
- 关键问题:An obvious question is how to choose the magnitude x below which to prune
- 相关工作:
- fixing a weight budget and keeping the top-k weights globally or per layer
- learn sparsification thresholds per layer,将模型的参数替换成下式,模型参数和每层的裁剪阈值一起训练
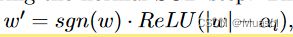
- reinforcement learner to derive the best values for each layer
- fix a weight to zero if the SGD optimizer would flip its sign during training
- prune whole filters with the smallest sum of absolute weights in convolutional layers
- prune recurrent neural networks
- lottery ticket hypothesis
- Han et al. (2016b) popularized magnitude pruning for modern deep neural networks as part of neural network compression for inference.
- 特点:
- based on the structure of the network:
- merge similar neurons
- Coreset pruning
- based on magnitude
- data-free methods的缺陷:expensive retraining to recover an accuracy as close to the original performance as possible
- 改进的方向:An obvious way to improve precision is to consider the influence of the training data (and implicitly its distribution) in the pruning selection.
3.3 Data-driven selection based on sensitivity
- intuition:Elements with very small or zero change with respect to deviation of the input examples contribute less in the entire network since their outputs are approximately constant to the variation in their inputs.
- 相关工作:
- based on input or output sensitivity
- output sensitivity(移除之后output不受影响):
- removes neurons that show very little variation in their output across various input examples. After removing, we add their output to the next neurons’ biases
- compute new weights for all units that consumed the output of the removed unit to minimize the change in their inputs. They pose the problem using a least-squares metric and optimize it with a conjugate gradient method
- model the outputs of hidden units as linear combinations of outputs of other neurons. A neuron can be pruned if its output is well approximated by a linear combination of other units’ outputs
- in convolutional networks:
- prune filters that, across the whole minibatch, change the output of a layer least
- use “centripetal SGD” to train the network towards similar filter weights that can later be pruned.
- use a geometric interpretation and find filters that are close to the geometric median of all filters
- sensitivity of neuron outputs with respect to elements in earlier layers
- the output sensitivity of a neuron with respect to deviations in its inputs
- sensitivity matrix S that captures the change of a neuron i in a layer k with respect to small perturbations of a neuron j in an earlier layer l
- contribution variance:
- if a connection has little variance across all training examples, then it can be removed and added to the bias of the target neuron
- prune “low-energy” neurons
- Average Percentage of Zeros:prunes neurons whose activations are mostly zero for many examples
- variation of model output depending on variation of each weight
- output sensitivity(移除之后output不受影响):
- based on activity and correlation:merge neurons that have very similar output activations and simply adapt their biases and rewire the network accordingly(similar as “merge similar neurons” in 3.2)
- identify such pairs of similaroutput neurons across the training examples and remove redundant ones
- use either Principal Component Analysis or KL divergence to compute the number for each layer and then remove the most correlated neurons or filters.
- preferentially drop weights between weakly correlated neurons and maintain connections between strongly correlated neurons.
- based on input or output sensitivity
- 缺点:they purely aim at minimizing the impact on the inputoutput behavior of the network. Thus, if the network has a low accuracy, it will not gain from such pruning methods
- 改进之处:consider the training loss function itself in the pruning process and use it to preserve or even improve the model accuracy of the pruned network as much as possible.
3.4 Data-driven selection based on 1st order Taylor expansion of the training loss function
- 基础:扰动参数前后的损失函数变化,可以用泰勒展开表示成:
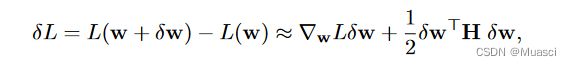
- total weight change
- Molchanov:use a squared gradient-weight product as first-order approximation to a neuron’s or filter’s importance. The intuition is that if weights are changed little from their initial random values during the network’s learning process, then they may not be too important
- binary gating function:
- two backprop stages
- absolute value of gradients
- Tri-state ReLU
- Jacobian matrix:
- QR factorization of jacobian matrix(both approaches benefit from the nonlinearity (e.g., sigmoid or ReLU) creating the rank deficiency due to saturation or cut-off)
- transfer learning:
- Movement pruning
- global sparse momentum:the important set is updated with the gradients during backprop;the other set does not receive gradient updates but follows weight decay to be gradually zeroed out
3.5 Selection based on 2nd order Taylor expansion of the training loss function
- 简介:Relative to the work in the previous section, these frameworks also focus on the question of which parameter to remove in order to minimize the corresponding loss increase
- optimization task:
- 其它跳过,公式太多了…
3.6 Selection based on regularization of the loss during training
- 常见的正则化方式:
- weight decay
- 正则项用于裁剪的难点:
- The choice of penalty term is most crucial for the success of the method
- The resulting problem is often non-convex and can hardly be characterized theoretically
- tuning the regularization parameters often requires a delicate balancing between the normal error term and the regularization term to guide the optimization process
- L0 NORM
- differentiable non-negative stochastic gating variables
- Estimating discrete functions
- Straight-through Estimators
- "softer” selection functions such as the Leaky ReLU or Softplus
- parameterizable continuous approximations:Heaviside step function
- directly learn the threshold for magnitude pruning during training
- top-k:
- top-k weights by magnitude
- select layers to sparsify
- polarization
- L1 NORM
- 特性:While L1 norms lead to very small weight values, they usually do not reduce weights to exactly zero and magnitude-based thresholding is often used to sparsify models
- Hoyer regularizer
- shrinkage operator
- Layer-wise regularization:they use the “cut off” to provide a convex relaxation to this optimization problem
- Grouped regularization
- lasso
- other:
3.7 Variational selection schemes
- Sparse Variational Dropout
- Molchanov:explicitly learns individual dropout rates αij for each weight wij
- Srivastava:regular binary dropout
- 优点:
- no additional hyperparameters need to be tuned
- without additional fine-tuning of the sparse network
- 缺点:
- this new model has twice as many parameters as the original network
- difficulties in training the model from scratch
- 优点:
- Structured Bayesian pruning:If the goal is acceleration, then structured sparsity is a more desirable outcome
- Soft weight sharing:combining soft weight sharing(compress a neural network by assigning its weights to different clusters)with pruning to compress neural networks
- Bayesian pruning with hierarchical priors
- Bayesian pruning for recurrent neural networks
- Related methods
3.8 Other selection schemes
略
3.9 Parameter budgets between different layers
- global selection:
- global selection without differentiating layers performs best for pruning of RNNs
- earlier layer-wise selection requiring to tune potentially complex hyperparameters
- especially for networks with very different layer types, convolutional and densely connected, different layers should be treated differently
- even the same layer types should be sparsified differently depending on their position in the network
- later layer-wise selection:
- automatically determine a good parameter budget per layer to reduce the hyperparameter complexity、
- link the sparsity to properties of the layer, such as the ratio of weights to neurons or kernel dimensionality
- computation performance:
- different layer types can have very different computational intensities
- two models with the same overall sparsity can have dramatically different operational (flop count) requirements
4. Dynamic Pruning: Network regrowth during training
4.1 Random or uniform regrowth
- activate a random weight during training:They also draw parallels to biological brains and argue that weight removal can be seen as natural selection, similar to synaptic shrinking during sleep(prune);weight addition can be seen as natural mutation(add)
- layer-wise addition:add parameters preferentially in layers that would be sparsified less
- uniform addition:Uniformly adding filters or neurons via a “width multiplier” to layers
4.2 Gradient information based
- gradients computation:
- keep a full copy of all weights up to date during training and only deactivate them with a mask in the forward pass
- restricts the flow of gradient information through pruned weights,gradients flow to pruned weights but their contribution is not forwarded to other weights
- compute a momentum term that captures gradients over multiple iterations as a criterion for growing weights
- reduce gradient storage:略
4.3 Locality-based and greedy regrowth
略
5. Ephemeral Sparsification Approaches
模型的稀疏模式视输入样本而定
5.1 Sparsifying neuron activations
- ReLU
5.2 Dropout techniques for training
- dropout
- Concrete Dropout:uses the Concrete distribution instead of Bernoulli sampling
- Variational dropout:uses Bayesian principles to define a variational dropout probability specific to each neuron based on measured noise during training, foregoing the data-free property of dropout to reduce the gradient variance
- Gomez:rank weights and neurons (activation outputs) by their magnitude and apply dropout only to a fraction of those deemed less important
5.3 Gradients
The key intuition is that the gradients produced by SGD are noisy, and therefore identifying and removing unimportant sub-components should not have a significant impact on convergence or may even have a regularizing effect, while enabling compression(reduce communication bandwidth).
5.3.1 Magnitude-based gradient sparsification
- A fixed threshold
- error feedback
- top-k selection
- compression is applied separately to subsets of a layer’s gradients
5.3.2 Variance-based gradient sparsification
5.3.3 Other methods for gradient sparsification
5.3.4 Convergence of sparsified gradient methods
5.3.5 Runtime support for sparse gradient summation
5.3.6 Gradient sparsification for better accuracy
5.4 Errors and optimizer state
In addition to the gradients of parameters, the gradients of a layer’s input, or the “errors”, can also be sparsified.
5.5 Dynamic networks with conditional computation
- PackNet and Supermasks:encode many tasks into the same dense network while circumventing catastrophic forgetting by using task-specific sparse subnetworks
- trained (data dependent) gating techniques
- use switching methods that explicitly select the next “expert”:
- MOE:
- GShard:600B
- Switch transformers
- MOE:
- product key networks
6. Sparsifying Particular Neural Network Architectures
6.1 Sparsifying convolutional neural networks
6.1.1 CNN architecture evolution
- GoogLeNet
- Inception
- Inception V3 CNN
- depth-wise separable convolution
- parameter-efficient MobileNets
6.1.2 CNN sparsification techniques
- Sparsify after training
- Han:magnitude-based sparsification, quantization, weight sharing, and Huffman coding
- a fully-sparse training approach could not match the performance of the dense-trained, then sparsified network
- with a sparser model, the randomized initial values of the weights play a more significant role than in a dense model. Thus, training a sparse model appears to be more prone to converge to suboptimal local minima than a dense network(tickets hypothesis)
- Sparsify during training
- Guo:the process of sparsification can benefit from re-adding weights during training that were “erroneously” pruned
- Sparse training
- Sparsifying parameter-efficient networks
- soft pruning
6.2 Sparsifying transformer networks
6.2.1 Structured sparsification
- heads
- Louizos:simple stochastic gating scheme to prune heads
- Michel:a first-order head importance score for pruning
- feedforward networks
- remove attention heads and slices of feedforward and embedding layers and use a gating mechanism(McCarley)
- all weight matrices(Wang)
- layers
- LayerDrop
6.2.2 Unstructured sparsification
- Prasanna: first-order importance metric | unstructured magnitude pruning typically results in networks that are both smaller and retain better accuracy
- Gordon: one need only prune BERT once after pretraining instead of for each downstream task
- Chen:magnitude pruning can prune a pretrained BERT model to up to 70% sparsity without compromising performance on the pretraining objective, and that such networks transfer universally to downstream tasks
- Sanh:Movement pruning
6.2.3 Sparse attention
QK计算的复杂度为O(s^2),其中s是序列长度。根据Yun(2020),如果要降低为O(s),需要满足三个条件:1. every token attends to itself;2. a chain of connections covers all tokens;3. each token connects to all other tokens after a fixed number of transformer layers
- restricting attention to local neighborhoods
- star topologies
- combinations of strided and fixed sparsity patterns
- sliding windows
- local attention plus a fixed number of tokens that attend globally
- SAC:learns a task-specific sparsity structure using an LSTM edge predictor.
7. Speeding up Sparse Models
略
8. Discussion
8.1 Relation to Biological Brains
computers和brains的不同:
- the three-dimensional arrangement of the brain encodes structural information nearly for free and learns through neuroplasticity. Silicon devices cannot adapt their wiring structure easily, and thus the simulation of structural properties leads to overheads in terms of memory (encoding the structure) as well as compute (controlling the execution)
- the visual cortex does not utilize weight sharing like convolutional networks do, however, in silicon, it seems to be the most efficient technique given that weight sharing reduces redundancy during feature detection and enables reuse for performance
- While we currently use SGD to train networks, it remains unclear whether biological brains use similar methods. Recent discoveries have shown a possible relationship to Hebbian learning (Millidge et al., 2020) and argue that SGD may be biologically plausible, albeit some gaps remain (Lillicrap et al., 2020).
8.2 Permutation Groups and Information Loss
8.3 Sparse subnetworks for training and lottery tickets
8.3.1 Pruning is all you need - networks without weight training
8.3.2 Lottery tickets in large networks
- Liu et al. (2019b) showed that with the best learning rate for larger networks, keeping the original initialization does not improve the final accuracy over random initialization
- Gale et al. (2019) also could not reproduce the hypothesis for larger networks.
- Frankle et al. (2020b) later argue that a variant of the hypothesis “with rewinding” applies also to larger networks if one uses the values after some initial optimization steps at iteration
略
9. Challenges and Open Question
典型相关工作整理
layer-wise unstructured sparsity
《Soft Threshold Weight Reparameterization for Learnable Sparsity》
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第2张图片](http://img.e-com-net.com/image/info8/50e6d7c5a1f247a7a08db9d361f6117b.jpg)
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第3张图片](http://img.e-com-net.com/image/info8/9af4cfbbdaf1432d972b799f69f68a8d.jpg)
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第4张图片](http://img.e-com-net.com/image/info8/43eb9d072c4e45e3bea4fa397871bbee.jpg)
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第6张图片](http://img.e-com-net.com/image/info8/4084c129a7b647f1a9878d94dec140ea.jpg)
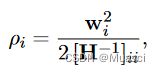
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第7张图片](http://img.e-com-net.com/image/info8/4b7100f0a6f147f88614136564365055.jpg)
![[文献阅读] Sparsity in Deep Learning: Pruning and growth for efficient inference and training in NN_第8张图片](http://img.e-com-net.com/image/info8/603bff63cf1d4c6c9c924f069549e9bf.jpg)