Texture Mapping for 3D Reconstruction with RGB-D Sensor(CVPR_2018) 中文翻译 论文带读

论文链接

Abstract

为3D模型获取逼真的纹理细节在3D重建中很重要。然而，由噪声的rgb-d传感器数据引起的几何误差的存在总是使得色彩图像不能精确地对齐到重建的3D模型上。在本文中，我们提出了一种全局到局部的校正策略，以获得更多期望的纹理映射结果。我们的算法首先为3D模型的每个面自适应地选择一个最佳图像，这可以有效地消除由多个图像混合产生的模糊和幽灵伪影。然后，我们采用非刚性的全局到局部校正步骤来减少纹理之间的接缝。这可以有效补偿由相机位姿漂移和几何误差引起的纹理和几何未对准。我们在一系列复杂场景中评估了所提出的算法，并展示了其在为3D模型生成无接缝、高保真纹理方面的有效性能。

1. Introduction

随着RGB-D传感器的出现，近年来3D重建取得了重大进展。虽然小规模对象和大规模场景都可以用令人印象深刻的几何细节建模 [10,17，26,27，28]，但3D模型的纹理恢复保真度仍然不太令人满意 [7,13，22]。

为什么纹理映射技术落后于3D建模？原因有四个: 1) 由于深度数据的噪声，重建的3D模型总是伴随着几何误差和失真。2) 在相机轨迹估计中，姿态残差会逐渐累积并导致相机漂移。3) 捕获的深度帧和色彩帧之间的时间戳不完全同步。4) RGB-D传感器通常分辨率低，色彩图像也容易受到光线和运动条件的影响。上述所有挑战都导致几何模型和相应图像之间的不对准，并导致不理想的映射结果。

虽然投影映射方法 [21,23] 可以减少由多图像混合引起的模糊和重影伪影，但由于几何配准误差和相机轨迹漂移，纹理出血在不同视图的边界上是不可避免的。Zhou和Koltun [30] 提出了一种使用局部图像扭曲的优化框架，该框架可以补偿几何错位。但是，这种方法需要细分网格模型，这将大大增加数据量并限制其应用范围。此外，多图像混合中通常采用的加权平均策略对相机快速移动引起的光变化和运动模糊敏感。

为了克服这些挑战，本文提出了一种新颖的纹理映射方法，该方法可以执行全局到局部的非刚性校正优化。首先，我们为每个面选择最佳图像，以避免多图像混合中的人为效果。在全局优化步骤中，我们使用联合的颜色一致性和几何一致性优化来从不同视图中校正每个纹理块的相机位姿。然后，在局部优化步骤中，我们为块的边界顶点找到了一个附加变换，以改善由几何误差引起的纹理坐标漂移。最后，我们采用纹理图集将纹理映射到所需的3D模型上。

我们验证了所提出方法在一系列复杂场景中的有效性，并显示出高保真的纹理。与方法 [30] 相反，我们的方法要快得多，并且需要的三角形信息要少得多。纹理模糊伪影也大大消除了。与 [23] 相比，我们的方法可以有效减少面边界之间的接缝不一致，并且可以容忍几何错位。

2. Related Work

纹理映射是获取逼真的3D模型的重要步骤 [11,16，26,29]。在本节中，我们将回顾一些改善纹理映射效果的相关方法。

基于混合的方法: 纹理映射的一种常用方法是采用不同的加权平均策略将多个图像混合成纹理 [3,8，20]。当前的rgb-d重建系统 [25,19，7] 主要依赖于截断有符号距离函数 (TSDF) 表示。这意味着，除了TSDF体积网格之外，他们还需要添加一个额外的颜色体积网格，以通过运行多个图像的加权平均值来计算每个顶点的颜色。但是，这使得这种方法对计算噪声敏感; 如果恢复的相机姿势或3D几何形状稍微不准确，则很容易出现模糊和重影。此外，模型细分的过程以及不同观点中模型大小的变化也会影响其性能。

基于投影的方法: 另一种机制是投影纹理映射，它将每个面或顶点与一个适当的图像相关联。Lempitsky等 [21] 使用成对马尔可夫随机场为每个面选择最优图像。受这项工作的启发，Allene等人 [2] 和Gal等人 [14] 引入了额外的度量来改进数据项和平滑项，以选择更合适的视图。但是，这些方法面临一个具有挑战性的问题，即如何减轻相邻面纹理之间的视觉接缝。为了克服这个问题，他们必须通过分别利用多频带混合 [6] 和泊松编辑 [15] 来添加后处理。Waechter等[23] 提出了一种全局色彩调整算法，以减少由视图投影引起的视觉断裂。虽然这些方法可以大大减少由多图像混合引起的模糊和重影伪影，但由于几何配准误差和相机轨迹漂移，纹理出血在不同视图的边界上是不可避免的。

基于扭曲的方法: 与上述方法不同，基于扭曲的方法对几何误差和相机漂移引起的未对准问题具有更大的抵抗力。Eisemann等人 [12] 通过估计投影纹理图片之间的光流，引入了一种局部纹理扭曲方法。Aganj等人 [1] 将不同的变形应用于不同的图像，以便拟合恢复的网格。通过薄板样条近似匹配不同视图中的特征点来计算位移场。此外，Zhou和Koltun [30] 设计了一个纹理映射框架，其中相机姿势和几何误差均通过局部图像扭曲进行校正。但是，这种方法需要细分网格模型，这将大大增加数据量并限制其应用范围。此外，由于仍在使用加权平均混合策略，因此这些方法还存在模糊的伪像。最近，Bi等人 [4] 使用基于补丁的合成为每个面生成新的目标纹理图像，以补偿相机漂移和重建误差，但是包含动态阴影的场景将是该方法的挑战。

3. Overview

这项工作的目的是将纹理图像映射到由商品深度相机获取的3D模型上。输入是包含深度帧和相应颜色帧的rgb-d序列或实时视频，输出是伴随高保真纹理的3D模型。为了实现这一目标并克服上述挑战，我们提出了一种全局到局部的优化策略，该策略包含四个主要步骤。图1显示了所提出方法的概述。

Input: 我们算法的输入是由Kinect v1获取的RGB-D序列或实时视频。有关更详细的颜色信息，还建议在Kinect的顶部添加一个额外的高清摄像头，以获得高分辨率的纹理图像。然而，为了公平地比较，我们仍然采用Kinect V1的低分辨率彩色图像作为实验输入。

Preprocess: 从输入深度序列中重建网格模型作为纹理映射的初始模型M0，并从原始颜色序列中提取帧子集作为纹理候选。为了提高质量和降低计算复杂度，与 [30] 不同，我们利用 [28] 来重建3D模型，而不是KinectFusion [18,22]，并通过加权图像清晰度，抖动，模糊和视口叠加的元素来选择纹理候选图像。该步骤产生一个初始模型M0和一组对应于所选色彩图像子序列 {Ci} 和深度图像子序列{Di} 的相机位姿 {T0 i}。

Optimization: 为了构建高保真纹理，我们的方法结合了 [23] 和 [30] 的优点。我们为模型的每个面选择最佳的纹理图像，以避免多图像混合引起的模糊。因此，通过将每个候选图像视为标签，我们将选择问题公式化为一个多标签马尔可夫场，其中包括相机位姿与法线映射之间的角度，投影区域以及从模型面到相机平面的距离。但是，由于T0和m0都不是绝对准确的，因此通常无法完全缝合具有不同标签的相邻面。为了解决这个问题，我们采用了全局到局部的优化策略。对于全局优化，我们根据相关块之间的颜色一致性和几何一致性来调整每个纹理块的相机位姿。在局部优化阶段，我们导入了一个额外的转换，以在不同块的边界上细化纹理坐标，并制作无缝拼接的纹理。

Texture Atlases: 最后，我们利用纹理图集将所需的纹理映射到3D模型上。在优化的相机位姿下，将每个面投影到其关联的纹理图像上，以获得投影区域。每个投影区域用于建立纹理图集，同时记录每个三角形面的顶点坐标。然后，我们将它们转换为图集空间。这样，可以通过纹理坐标在图集中直接检索每个顶点的纹理，并生成最终的纹理模型。

4. Texture Mapping Method

在本节中，我们将更详细地阐述每个步骤。令M0表示用于纹理映射的重建网格模型，{vi} 和 {fi} 分别是M0的顶点集和面集，其中每个面表示模型上的三角形网格。T是一个4 × 4变换矩阵，它将M0的顶点vi从世界坐标变换为局部相机坐标，定义为:

其中R是3 × 3旋转矩阵，t是3 × 1变换向量。
我们还将3D顶点v = [x，y，z]T在2D图像平面上的透视投影指定为 Π。因此，在图像平面上顶点v的像素坐标u(u，v)可以被计算通过：

其中K是相机内部矩阵，fx，fy是焦距，cx，cy对应于小孔相机模型中相机中心的坐标。此外，我们使用D表示深度图像，C表示色彩图像，I对应于色彩图像的强度。

4.1. Model Reconstruction

我们管道的输入是深度图像流和伴随的RGB颜色序列。在我们的系统中，我们使用Microsoft Kinect V1来捕获这些数据。由于Kinect V1的输入帧分辨率低，并且容易受到运动模糊和抖动效应的影响，因此我们选择了高可信度帧的子集用于场景建模和纹理映射。
我们的方法利用稀疏序列融合 (SSF) 方法 [28] 代替KinectFusion [18,22] 来重建初始3D模型并提取高可信度的颜色帧。此方法考虑了抖动，模糊和其他一些导致扫描噪声的因素。它可以用稀疏深度图像序列 {Di} 重建网格模型M0。[28] 的基本功能定义如下:

其中Esel(i) 是开关项控制深度图像Di的选择。如果将当前图像视为要集成的有效图像，则应将其设置为1，否则为0。Ejit(i) 通过计算选定图像之间的即时视点变化来测量抖动效果。连续性项Edif(i) 是通过计算相机位姿变化来确保两个选定支持图像之间有足够的场景重叠，并且Evel(i) 评估相机运动速度。除了这些元素之外，为了获得高清晰度的图像，我们还引入了一个术语来描述每种颜色帧的质量。等式4显示了我们用于帧提取的目标函数:

其中Essf是SSF项，λ cla是平衡参数。我们在实验中使用 λ cla = 10，其他的是根据 [28] 设置的。清晰度术语Ecla定义为:

模糊值 θ 通过 [9] 计算。等式5示出，一旦深度图像Di被添加到支持子集中，其对应的色彩图像Ci的清晰度必须要被计算；否则，根据Esel(i) 的值直接忽略。迭代继续进行，直到处理完所有捕获的图像。这将产生具有关联的相机位姿{T0 i} 的稀疏色彩图像序列 {Ci}，可以用作纹理候选。

4.2. Texture Image Selection

许多纹理映射方法 [3,8，20] 将网格投影到多个图像平面上，然后采用加权平均混合策略从像素 [11,16] 合成模型纹理。他们理想地假设估计的几何表面和相机姿势足够准确，但是在实践中，这很容易被违反。因此，我们不是直接从多个图像中合成，而是分别为模型m0的每个面部选择一个最佳纹理图像。通过将每个候选图像视为标签，我们将此选择问题公式化为基于 [2] 的成对马尔可夫随机场 (MRF):

数据项Ed将每个模型面投影到每个候选图像Ci上，并测量投影区域的面积，该面积与角度视图接近度、角度、图像分辨率和可见性约束有关，定义如下:

平滑项Es，由公式描述，如8所示，计算沿边缘e的积分以测量颜色差异，其中e是分配给不同纹理图像 (Ci，Cj) 的相邻面之间的公共边。ε 是模型m0的整个边集。
公式的等式6的MRF函数E（C）用图形切割和阿尔法展开最小化 [5]。

4.3. Global Optimization

上述步骤将每个面与纹理图像Ci相关联。但是，由于几何误差和相机漂移的存在，直接使用纹理拼接或颜色调整后处理 [21,14] 无法使相邻面上的纹理在视觉上保持一致。这是投影纹理映射方法的主要挑战。为了消除视觉接缝，我们借鉴了非网格校正的思想，以在相邻面之间缝合纹理。

通过外在矩阵T0和内在矩阵K，可以轻松地将模型面投影到它们的关联图像中，以获得纹理颜色。然而矩阵 {T0 i} 总是嘈杂的，因此，通过这些变换获得的纹理颜色也可能不准确。因此，在本节中，我们必须优化 {T0 i} 以确保来自不同纹理图像的所有面都可以紧密对齐。

我们首先基于纹理图像 {Ci} 执行面的聚类过程，也就是说，如果两个相邻的面对应于同一纹理图像，我们将它们放在同一带标签的聚类中。遍历所有面后，可以获得簇的集合，如图2所示。为了清楚起见，我们将同一群集中的所有面命名为chart 。为了提高鲁棒性，如果chart i中的面Fi的数量小于阈值FN，则该chart将被合并到其最接近的邻居j中，该邻居j由三方面的因素测量: 1) chart i和j的纹理图像之间的视点角度应该是最小的。2) 面数符合Fj> FN的标准。3) 图表i中所有顶点在图表j的纹理图像上的投影仍应保持在边界内。在随后的实验中，我们凭经验设置FN = 50。基于聚类，我们从chart 中建立一个无向连接图G; 如果两个图表彼此相邻，则将有一个边gij ∈ G链接它们。

chart 内的面的纹理来自同一图像，因此它们对齐良好。这意味着，为了为模型生成自然纹理，我们只需要调整不同chart 之间的纹理。对于理想的纹理映射，我们认为一个chart 的边界纹理可以通过其相邻chart 的纹理完全恢复。基于此观察，只要有可能最大程度地减少每个chart及其邻居的关联纹理和投影纹理之间的不一致，我们就可以对齐相邻的chart 纹理。但是，仅考虑颜色一致性可能会导致无纹理区域的未对准。因此，我们还考虑了几何一致性，它是等式9中的正则项。如下，我们通过测量每个chart 的颜色一致性和几何一致性构造出目标函数公式。

其中vk表示chart i中的整个顶点集，N是其编号。chart N表示模型m0上的chart 数量。函数 φ (x) 计算向量x的Z分量。Gi描绘了chart i的邻域。第一项使chart i的纹理与其相邻chart j的投影纹理一致。第二项确保，当T改变时，优化的相机位姿不仅使纹理一致，而且重建的模型要与RGB-D相机获取的深度图像保持一致，并在颜色约束不足时确保相机位姿T不会偏离初始值T0。通过最小化等式9，我们可以为每个chart 计算一个校正变换矩阵，这使得相邻的chart 彼此更接近，并减少视觉接缝。

4.4. Local Optimization

虽然全局优化能够使大多数纹理区域缝合，但对于具有较大几何误差的一些区域 (如图1© 的红色框所示)，纹理仍然不能精确地对齐。全局优化只能校正每个chart 的相机漂移。如果重建的几何模型足够精确，则在全局优化之后，所有纹理都将被很好地缝合。不幸的是，几何误差的普遍性使得仅有的全局优化不足以实现高保真纹理映射。因此，我们在模型的每个面上引入了进一步的调整，以便也可以很好地对齐局部纹理。

因为一个chart 上的所有面都对应于同一纹理图像，因此不需要优化整个图表。此外，由于在全局优化步骤中已将每个图表大致对齐，因此仅需要对一小部分顶点进行校正，以弥补由几何误差引起的纹理未对齐。我们建议修改每个chart 中边界顶点的投影坐标，而不是编辑网格模型。如图3(b) 所示，为了在顶点v处对齐纹理，我们可以在图像A中移动v的投影坐标以在图像B中对齐v的纹理。只要优化了边界顶点，整个chart 的纹理就会很好地对齐。

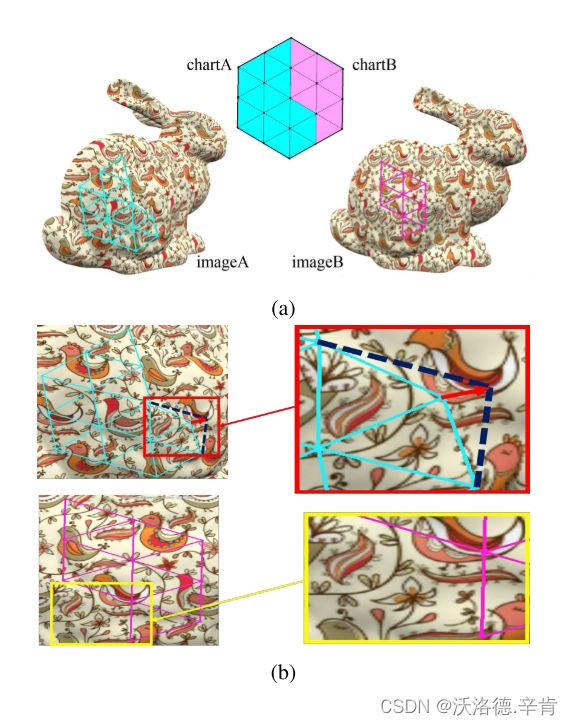
但是，移动顶点的投影坐标是一个不适定的问题。为应对挑战，我们找到每个边界顶点的纹理坐标的最佳移动向量，并使其与其相邻的chart 纹理对齐。为此，我们为chart 边界上的顶点v计算一个额外的变换矩阵，而不是直接计算移动矢量。附加变换确保顶点v所在的chart 与连接到v的chart 充分对齐。然后我们使用此矩阵来获得v的最佳投影坐标作为纹理坐标。纹理坐标校正过程能够使每个边界顶点v处的局部纹理充分对齐。我们设计一个目标函数来计算v矩阵以校正图像中的纹理坐标，如下所示:

其中j代表chart i的边界顶点，k代表共享顶点j的i的相邻chart ，v代表chart i中的整个顶点。Tij是一个额外的变换矩阵用于校正顶点j的纹理坐标，使顶点j在chart i中的投影纹理与相邻chart k的纹理图像上的投影纹理一致。Ti和Tj是通过全局优化对chart A和chart B进行优化的变换矩阵。I表示单位矩阵。第一项是数据项，它使chart 边界上的顶点的纹理尽可能对齐。第二项是正则项，它确保附加矩阵不会偏离全局优化的结果。

我们使用高斯牛顿迭代来求解方程9和10。我们得到全局优化后每个chart 的相机变换Ti。对于chart 边界上的一个顶点，我们获得了一个额外的变换来校正投影的纹理坐标，这可以使纹理与该顶点处相邻面的纹理对齐。然后，我们重复该过程，直到处理完所有边界纹理坐标。

整个chart 可以通过Ti投影到纹理图像以获得纹理坐标，对于chart 边界上的顶点，我们进一步使用变换Tij进行非刚性校正以获得校正后的纹理坐标。我们保存纹理坐标并获得纹理图集。最后，使用纹理图集技术，我们可以生成无缝纹理模型。

5. Results

略

6. Conclusion

在本文中，我们提出了一种非刚性纹理映射方法通过RGB-D传感器重建三维模型。我们方法的输入是RGB-D视频序列，输出是具有高质量纹理的3D重建模型。我们引入了全局优化步骤来调整纹理位置，并设计了局部优化以进一步细化纹理边界。实验表明，即使在具有挑战性的场景中，我们的方法也可以产生高保真的纹理模型。将来，我们希望将视觉显着性信息 [24] 导入我们的框架中，以进行更详细的纹理恢复。

7.References

略。