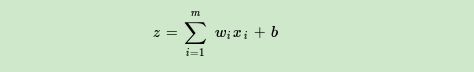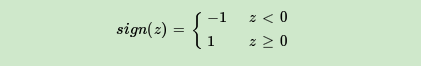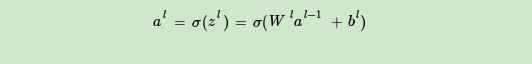深度神经网络DNN的理解

1.从感知机到神经网络

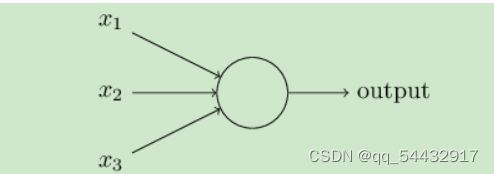
上图是一个感知机模型，有若干个输入和一个输出（输出的结果只可以是1或-1）

输入和输出有一个线性关系：

神经元激活函数：（二分类）

 由于这个简单的感知机只可以进行二分类，则对于感知机进行升级，升级如下：

1）加入隐藏层，从而增加模型的表达能力，同时也增加了模型的复杂度

2）输出层的神经元不止一个输出，可以有多个输出

3）扩展了激活函数，从感知机的激活函数sign（z）---->sigmoid，之后又出现了tanX，softmax，ReLu等，通过不同的激活函数提高了神经网络的表达能力

2.深度神经网络（DNN）的基本结构

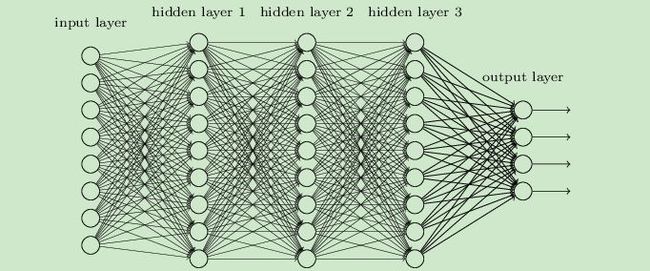
 神经网络是基于感知机的扩展，深度神经网络就是有很多隐藏层的神经网络，所以深度神经网络也叫做多层感知机。

深度神经网络的内部神经网络有3层，第一层输入，最后一层输出，其余中间都是隐藏层，层与层之间全连接。在局部的小模型来讲和感知机是一样的，都是线性关系+激活函数，即

Layer 1:                                                                Layer 2:

Z[1] = W[1]·X + b[1]                                            Z[2] = W[2]·A[1] + b[2]
A[1] = σ(Z[1])                                                      A[2] = σ(Z[2])

X其实就是A[0]，所以不难看出：

Layer i:
Z[i] = W[i]·A[i-1] + b[i]
A[i] = σ(Z[i])

（注：σ是sigmoid函数）

因此不管我们神经网络有几层，都是将上面过程的重复

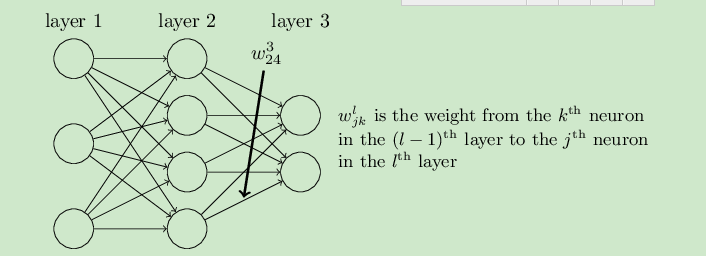
系数w的定义：

如下图：这里的w243指的是第二层的第四个神经元到第三层的第二个神经元

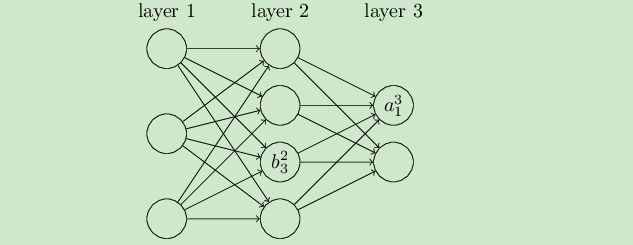
偏置b的定义：

如下图：b23表示第二层的第三个神经元，a13表示第三层的第一个神经元

3.深度神经网络前向传播算法的原理

核心：利用上一层的输入计算下一层的输出

以上是代数法，其实一个一个表示输出很复杂，所以就有了简化版的写法，就是矩阵法。

假设第l−1层共有m个神经元，而第l层共有n个神经元，则第l层的线性系数w组成了一个n×m的矩阵Wl，第l层的偏倚b组成了一个 n×1 的向量 bl ，第l-1层的输出 a 组成了一个 m×1 的向量 a（l−1），第l层的未激活前线性输出z组成了一个 n×1 的向量 zl ，第l层的输出 a 组成了一个 n×1 的向量 al 。 

4.深度神经网络的前向传播算法

利用若干个权重系数矩阵w，偏置向量b来和输入值向量x，进行一系列的线性运算和激活运算，从输入层开始，一层一层向后计算，运算到输出层得到输出结果

5.深度神经网络反向传播算法要解决的问题

假设有m个训练样本 {(x1,y1),(x2,y2),...,(xm,ym)} ，xi为输入向量，其特征维度是n_in；y为输出向量，其特征向量为n_out。用m个样本训练出一个模型。当有一个新的测试样本（Xtest，Y？）的时候，预测Ytest的输出。

我们使用深度神经网络模型，使输入层有n_in个神经元，输出层有n_out个神经元，再加上含有若干个神经元的一些隐藏层。现在的目标就是要找到所有隐藏层和输出层对应的线性系数矩阵w和偏置向量b，让所有训练样本输入计算出的结果（输出）尽可能的接近或等于样本的输出。通俗来讲就是你的训练集已经放进了一个完美的标注Ym，神经网络在训练的时候会也会训练出一个标准，用神经网络那个标准与Ym相比对，会产生一定的差距。损失函数就是Ym结果与神经网络训练出的模型具体差多少的定量表达。一般损失函数比较两个模型差距多少的三种思路是：最小二乘法，极大似然估计法，交叉熵法。对损失函数进行优化求最小化的极值，对应的一系列w和b即为最终的合适的参数。而这个损失函数的优化极值求解过程最常见的一般是通过梯度下降法来步步迭代。

6.深度神经网络反向传播算法的基本思路

在进行反向传播算法前，我们要选择一个损失函数，来度量训练样本计算出的输出与真实训练样本输出的损失。深度神经网络可以选择的损失函数很多，要选择一个损失函数来用梯度下降法迭代修改每一步的w和b。具体的思路很复杂 ，我暂时还不能很好的理解，请读者见谅！

7.深度神经网络反向传播算法过程

输入：总层数L，各隐藏层与输出层的神经元个数，激活函数，损失函数，迭代步长a，最大迭代次数max与停止迭代阈值，输入的m个训练样本

输出：各隐藏层与输出层的线性关系系数矩阵w和偏置向量b

8.均方差损失函数+sigmoid激活函数的问题

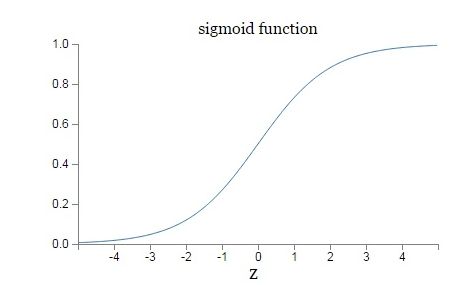
在讲反向传播算法的时候，我们用均方差损失函数和sigmoid激活函数做了实际例子，但是其实这是有问题的。

看上图，如果z取值越来越大，函数曲线变得平缓，意味着导数 σ′(z) 也越来越小。而在反向传播过程中，每一层向前递推都要乘以导数 σ′(z)得到梯度变化值sigmoid这个曲线就意味着在大多数时候梯度的变化值很小，导致算法收敛速度较慢。那怎么解决这个问题呢？

9.改变损失函数和激活函数

损失函数3种：最小二乘法，极大似然估计法，交叉熵法

激活函数：sigmoid，tanX，softmax，ReLu...

根据经验，应该两两搭配换着；来试一下，哪个效果好选哪个

10.参考资料

深度神经网络(DNN) - 知乎 (zhihu.com)