数据库学习笔记

ppt下载

ppt 提取码：cyyy

数据库系统概述

数据

数据本质上是对现实世界的编码，与现实一一对应，数据由各种成分组成，都是字段。

数据管理

1. 人工管理：程序与数据集1对1
2. 文件系统：以系统为中介，链接程序与文件
3. 数据库系统：以DBMS为中介，且文件被封装为一个整体（DB）
4. 大数据：正在发展

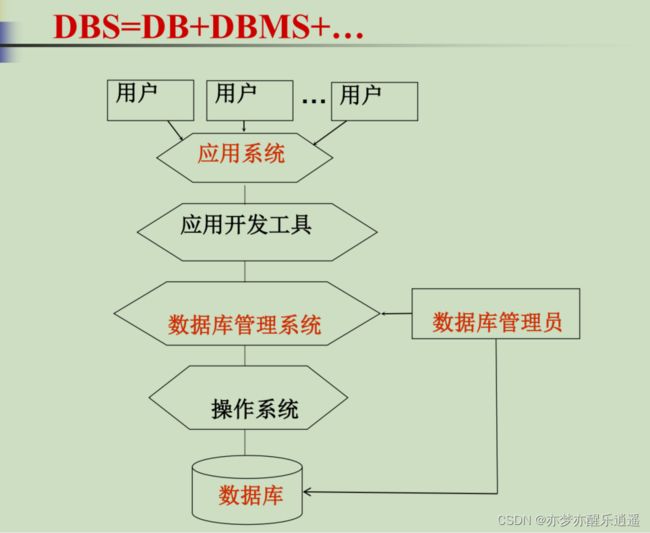
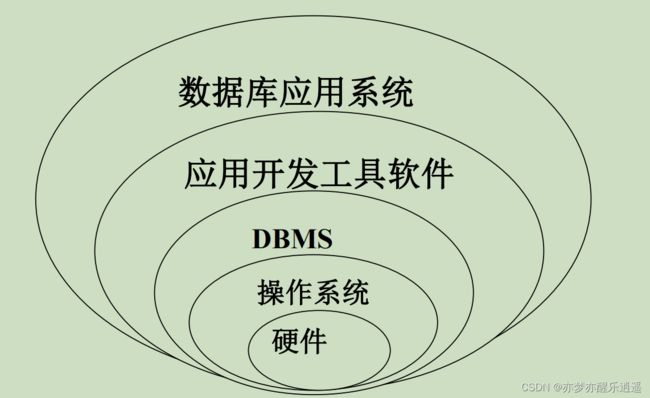
数据库

优点：

1. 继承了前面的储存，有组织
2. 发扬了结构化，独立性（解耦），减少冗余，提高了数据容量
3. 增加了共享性，安全保护。

简言之，数据库高度抽象，建立程序与数据之间的通道。

通常来说，数据库指DBMS。

发展：

1. 层次，网状数据库。
2. 关系数据库。Oracle，MySQL，SQL Server等等。
3. 新型数据库。解决数据量变大，以及网络环境的。网络的，分布式，面向对象的，多媒体的。NoSQL，NewSQL。

数据模型

三要素：

1. 数据结构，即基本的组织方式，数据定义，这个是最基本的。
2. 数据操作，CRUD+其他高级操作
3. 完整性约束，这个个人感觉是区别与文件系统的核心，更复杂，更抽象。

三要求：

1. 真实模拟
2. 便于链接人（让人理解）
3. 便于链接计算机（在计算机上实现，让计算机理解）

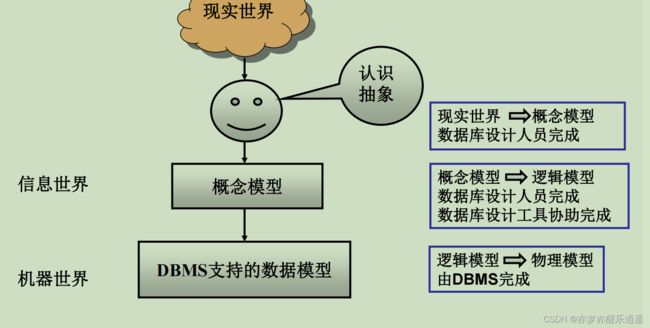
分类：

1. 概念模型：最顶层的设计，产品端提出要求，和具体实现无关
2. 数据模型：和DBMS设计关系较大，比如有层次模型，网状模型，关系模型，面型对象数据模型，对象关系数据模型，半结构化数据模型。

基本数据模型（前面的2）也分两层：

1. 逻辑数据模型：相当于定义DBMS的一些操作，概念。
2. 物理数据模型：具体在操作系统上实现DBMS。

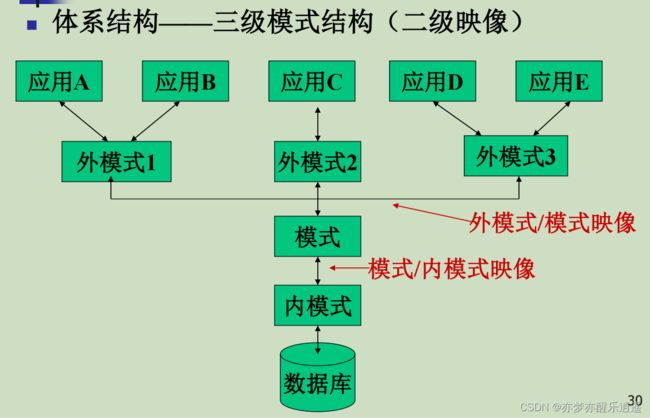
数据库系统结构

（视图）外模式：与视图对应，又名子模式，与程序，用户绑定。

外模式-模式映像：用户级。接口。

（概念）模式：综合所有数据，是一种逻辑上的全局描述。

模式-内模式映像：管理员，设计师级。接口。

（物理）内模式：是模式的物理实现的描述。

操作系统：将硬件操作封装，通过物理内模式描述来操作数据库。

物理数据库：文件。

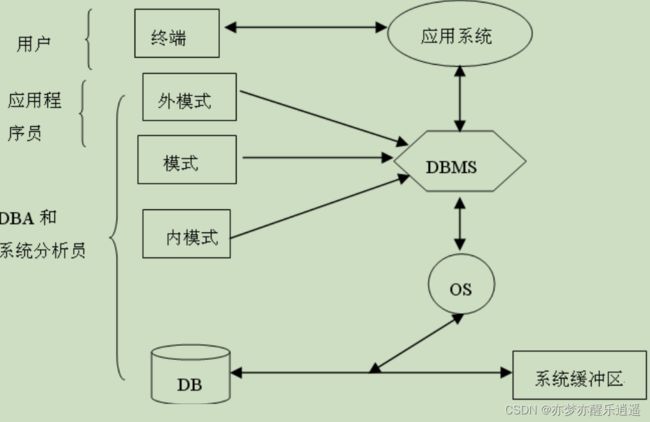
DBMS

这门课主要学习DBMS，后面会逐章学习。

1. 定义功能
2. 操纵功能
3. 保护功能
4. 维护功能

数据模型

基础概念

核心：

将现实事物抽象为数据，并将现实中事物之间的联系抽象为数据之间的联系。说白了就是用数据去复刻现实，在此之上添加更多的操作。

内容：

1. 概念模型：最顶层的设计，产品端提出要求，和具体实现无关
2. 数据模型：和DBMS设计关系较大，比如有层次模型，网状模型，关系模型，面型对象数据模型，对象关系数据模型，半结构化数据模型。

基本数据模型（前面的2）也分两层：

1. 逻辑数据模型：相当于定义DBMS的一些操作，概念。
2. 物理数据模型：具体在操作系统上实现DBMS。

实现步骤：

按照上面的结构自顶向下逐层分解，直到实现。

E(ntity)-R(elationship)概念模型（基础）

这个是朴素的关系思想，和知识图谱非常像。

基本概念

实体：

1. 实例：某个具体的东西，或者是一个抽象的概念（比如一节课）
2. 实体集（set）：同类实体（实例）集合，这里应该是一张表。
3. 实体型（type）：名字+若干特征，用于描述一个实体集的特征。

属性：

1. 属性的类型：就是字段
2. 属性的值：字段的具体值
3. 属性的域（domain）：属性的定义域
4. 特殊属性-键（key）：独一无二，实体id

实体间的联系：

1. 实体内部联系：各属性之间联系
2. 实体之间联系：各实体集之间的联系，往往是一个动作描述，这一点和实际不同，在计算机中我们只关注大类。
3. 两个实体集之间的联系从数量上说，有链式，树式，图式。当然也可以多个实体集有联系。实体集内部不同实体也可以有联系。

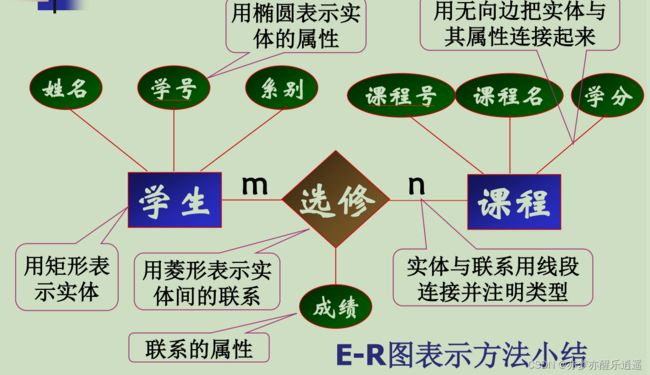
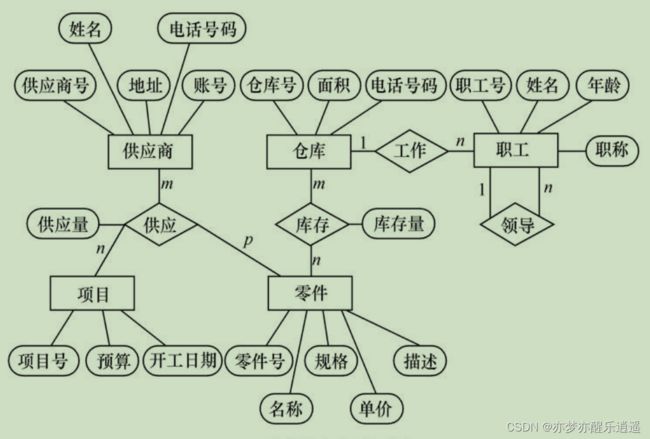
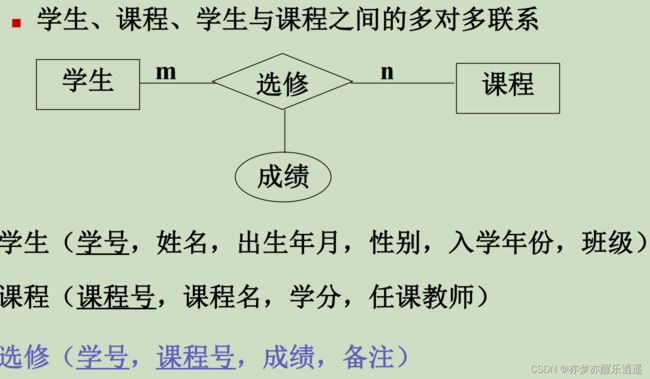
E-R数据模型

图形表示：

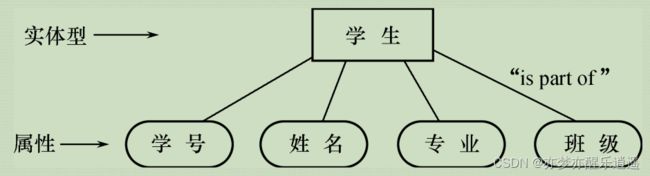
1. 实体用矩形——无向边链接——属性用椭圆
2. 联系用菱形，无向边链接实体集，上面注明连接类型（链树图）。
3. 联系本身也算实体，所以也有属性。

联系的语义：

1. 基数比约束。就是几对几
2. 参与约束。描述完全参与或者部分参与
3. 参与度：实体集中的某个实体参与联系的最小次数比最大次数。基数比约束和参与约束都可以通过参与度统一表示。

弱实体：

1. 类比面向对象中的组合。就相当于把实体中的一些属性弄出来变成新的实体，但是这个实体是对原实体依赖的，是他的成员。比如家长，可以作为学生的属性，也可以提出来。
2. 依赖于其他实体存在的实体。
3. 实体，联系，连线都用双框表示

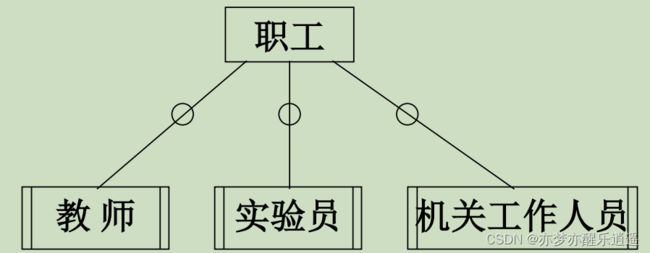
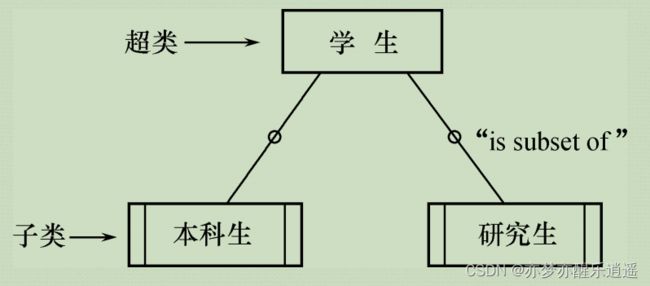
子实体：

1. 将基实体特例化。
2. 将超类分割为子类
3. 子类继承超类属性，联系
4. 子类之间也可以有联系
5. 表示方法如下：加两边短线表示孩子，然后用圆圈链接线。

模型综合举例：

层次数据模型

这是最早的，比较混沌。代表是，IBM的IMS。

特征

相比于E-R模型的图结构，层次结构是树形结构，有点面向对象的味道。

1. 只能处理一对多联系，多对多只能通过分解成一对多来实现。
2. 记录值必须按照路径查看，才有意义，有点huffman编码的味道。
3. 子女不能脱离双亲记录值独立存在，每次插入都必须从根部找下来，每次删除节点都必须递归删除所有子节点。
4. 每个记录类型定义一个排序字段，称为码字段

储存结构

1. 按照前序遍历的顺序，把所有记录值按照物理顺序存放。
2. 用指针直接将树结构储存。

点评

优点：

1. 数据结构直观
2. 查询效率高

缺点

1. 不能直接反应多对多联系
2. 插入删除效率低

网状数据模型

有点像E-R模型，是有向图结构。代表是DBTG系统。

层次模型可以说是网状数据模型的一个特例。

表示方法

1. 实体：用结点表示
2. 属性：用字段描述
3. 联系：用连线描述，多对多联系仍然是分解成一对多联系。

点评

优点

1. 图更容易模拟显示世界
2. 指针存取效率比较高

缺点

1. 结构会随着体量而逐渐复杂，冗杂
2. 操作不太容易
3. 编程实现不太容易

关系数据模型（主流）

IBM的研究员提出的，获得了图灵奖。

基本概念

1. 关系：基本数据结构单元是二维表，称为关系，可以用来描述一个实体集
2. 属性，域，同上。但是属性不可分是一个基本原则。
3. 元组：实体集中的一个个体，有包括Key在内的若干属性（分量）
4. 键：主键只能有一个，但是可以有多个候选键
5. 关系模式：用于描述一个实体集，形式为，关系名（属性名1，属性名2，…，属性名n），是实体的封装。
6. 关系数据库模式：一组关系模式的集合，是实体集的封装。
7. 关系数据库：一组关系模式所对应的关系的集合，是关系数据库模式的封装。

表示方法

1. 实体集用关系表示
2. 一切联系都用关系表示，一种朴素的想法就是，将两个被连接实体集的主键包含在关系中，表明联系，再加入额外的属性用来说明联系的更多信息。
3. 通过关系的组合可以模拟出各种复杂的联系

数据操纵

CRUD是基本，而且通过SQL语句高度封装，我们这里解释一下本质，对数据的全部操作都可以归结为对关系的运算。

也就是说，关系型数据库，实体是关系，联系是关系，操作还是关系操作，操作结果仍然是关系。

关系运算：

1. 关系代数
2. 关系演算

点评

优点：

1. 数据结构简单，概念单一
2. 建立在严格的数学概念基础上，具有良好的扩展性，可以建立复杂的架构
3. 存取路径对用户透明，数据独立性好，开发简单

缺点：

1. 查询效率一般，为此需要进行查询优化
2. 语义贫乏，难以描述特别复杂的对象（似乎和前面所说的复杂结构有所矛盾？）

面向对象数据模型（发展）

起源于OOP，将数据结构定义成对象，支持面向对象的各种层次结构。

但是有待研究，或许是未来的新的爆发点。

关系数据库

关系模型的基本概念

基本概念

1. 数据结构：现实中实体与实体之间的联系均用关系来表示
2. 逻辑结构：二维表，每一个实体集都是一张二维表
3. 数学基础：集合代数

关系的定义

基础概念

1. 笛卡尔积。若干个集合的笛卡尔积是这些集合的全排列，每一个位置上都可以出现该集合的任一元素。
2. 元组。Tuple，同Python里的写法，有n个元素则叫做n元组
3. 分量。元组里的元素被称为第i个分量.。写作$d_i$
4. （值）域。域是相对于分量来说的，即第i 个分量的取值空间称作第i 个分量的域。写作$D_i$。经常的，我们会对若干个域进行笛卡尔积运算。
5. 基数（cardinal number）。对于一个域，本身就是一个集合，自然有基数。写作$m_i$。 对于有限集，就是n，无限可列集就是${\aleph }_0$，无限不可列集$\aleph$。对若干个域进行的笛卡尔积也是集合，易得为$M=\prod m_i$

关系的概念

1. n个域，对应n个分量，对应n个属性。n个域的笛卡尔积可以产生M个n元组，这样就可以排列出M行n列的二维表。
2. 定义：$D_1\times \cdots \times D_n$的子集称为$D_1,\cdots ,D_n$上的关系。域笛卡尔积产生的二维表是全排列，实际上不一定用全排列，所以用子集作为关系。
3. 写作：$R(D_i,\cdots ,D_n)$，R为关系名，n为关系的度或者目，$D_1,\cdots ,D_n$为关系的域。联系一下离散数学，当n=2，则为二元关系。
4. 关系的每一行对应一个元组，用t 表示
5. 关系的每一列对应一个域，同时对应一个属性，记作$A_i$
6. $t[A_i]$表示元组t 在$A_i$属性上的值
7. $dom(A_i)$表示属性$A_i$的域

关系的特殊性

1. 分量的次序没有关系。可以用属性名绑定分量，这样无论如何排列，总能通过属性名绑定找到对应的分量。
2. 数学意义上的关系可以是无限的，但是实际上受到储存空间限制。
3. 关系必须是简单的二维表，每一列都不可分
4. 本质上，关系是一个笛卡尔积产生的集合，只不过被表达成二维表

规范化的关系

理论上规范化的关系应该有以下特征：

1. 一个属性必然属于一个域。同时多个属性也可以共享一个域。
2. 列次序无关紧要，行次序也无关紧要，重点在于关系本身。
3. 每个分量都是原子的，不可再拆分的。
4. 每个元组都是独一无二的，满足集合的不重性

实际上的DBMS不一定满足。

关系与关系模式

1. 关系的型：指关系模式（对标实体型），用来描述一种关系类型，写作$R(A_1,\cdots ,A_n)$，或者简单用R来描述
2. 关系的值：指元组的集合（对标实体集），就是关系的内容，是一种类型的具体表示。所以一般将关系r 写为$r(R)$，即建立在关系类型R上的一个关系值。

实际上，完整的关系模式不能简单用1来描述，而是$R(U,D,DOM,F)$

1. R：关系名
2. U：属性名集合
3. D：属性的域集合
4. DOM：属性名和属性域的映射，用来链接U与D
5. F：属性间的数据依赖关系集合。这个难以用二维表描述。

关系数据库与关系数据库模式

一个关系数据库中有p 个关系，所以数据库对关系是包含关系，据此引出以下概念

1. 关系数据库模式：$R=\{R_1,\cdots ,R_p\}$ （注意这里是大括号）。从这里可以看出，关系数据库模式就是该库中所有关系型的集合
2. 关系数据库：$d=\{r_1,\cdots ,r_p\}$。同上，关系数据库就是库中所有关系值的集合。

关系模式与关系统称为关系，根据上下文判断。

键

键定义和超键

属性名通常记作K

键的本质目的在于区分元组，即区分行。所以有一个硬性要求：$\forall t_1,t_2有t_1[K]\ne t_2[K]$

键的形式就是用于区分作用的属性或者属性组合。

1. 理想中的键就是一种一一对应，具有最小属性数。
2. 超键就是键的超集，超键是键，可以用于区分元组，但是超键允许冗余属性存在。

其他键类型

1. 主键与候选键与候补键：在n个候选键中选出1个主键与n-1个候补键
2. 候选键中的属性成为主属性，其他的称作非键属性（非主属性）
3. 联合键与全键：多个属性组成的键。如果是所有属性的联合键，那就是全键。
4. 外键：外键是属于另外一个关系的。具体来说就是，外键在被参照关系中。外键可以给出不同关系之间的联系。可以看这篇文章,外键其实就是约束了值的范围。

https://blog.csdn.net/sinat_41803693/article/details/84021238?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%A4%96%E9%94%AE&utm_medium=distribute.pc_search_result.none-task-blog-2_allsobaiduweb~default-1-84021238.142^v14pc_search_result_control_group,157^v14control&spm=1018.2226.3001.4187

关系的完整性约束

为了保证数据库与现实世界的一致性，需要维护完整性。

1. 实体完整性约束。即实体中不能有空的
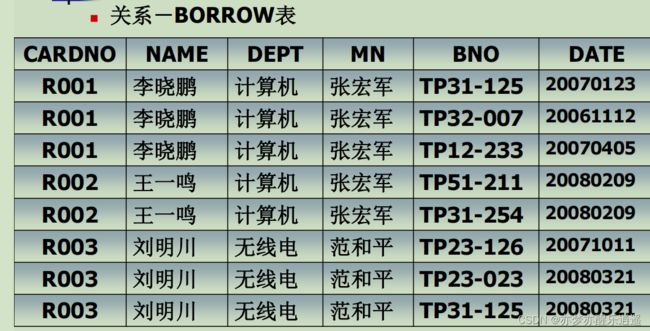
2. 参照完整性约束。描述两个关系的联系，一个关系是参照，含有外键，另一个是被参照，其主键作为参照的外键。比如这个右边就是一个被参照的，左边就是参照（别的关系的），每次参照都要取被参照的主键。
3. 其他约束。用户自定义后由系统支持。

关系代数

关系代数概述

1. 基础是集合代数，
2. 实际上是一种抽象的查询语言，用关系的运算来表达查询指令
3. 运算的对象与结果都是关系

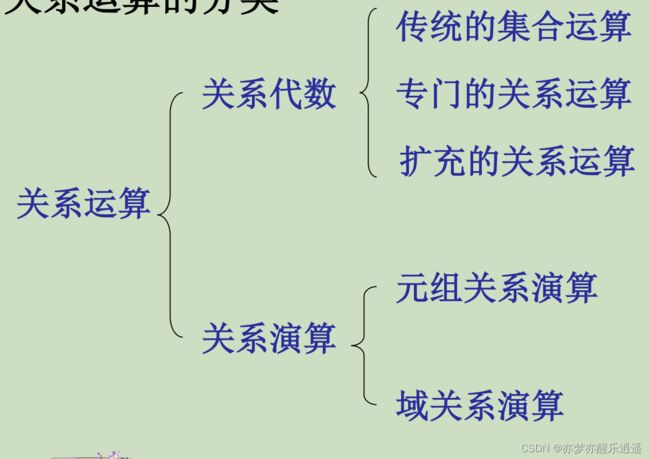
分类：

1. 传统集合运算。交并差，广义笛卡尔积，以及将元组作为元素来进行集合代数运算
2. 专门的关系运算。选择，投影，连接，除
3. 扩充的关系运算。为数据库应用而引进的特殊运算

传统的集合运算

并差交

对于同一个关系模型的两个关系进行运算，产生新的集合（关系）。同传统的并差交一样，保留集合的唯一性。

笛卡尔积

关系来源于对域的笛卡尔积。而我们这里的笛卡尔积又是对关系作用的，但是本质相通。

对于R与S的笛卡尔积，是针对每一个元组，进行全排列组合。

新关系的度数为原有度数之和，内容是元组拼接的全排列。

专门的关系运算

选择

对应select语句，条件就是一个布尔表达式，选出所有真值的行合并为一个新关系，是原有关系的子集。

写法：

1. ${\sigma }_F(R)=\{t|t\in R\wedge F(t)\}$

举例：

1. ${\sigma }_{age<20}(R)$，对R中年龄小于20的进行选择

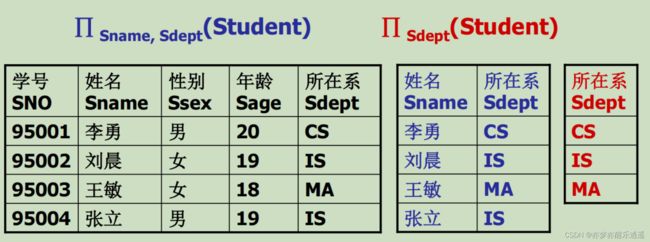
投影

选择是从行的角度提取，投影是从列的角度提取。提取一个属性集对应的关系。

写法：

1. ${\prod }_x(R)=\{t[X]|t\in R\}$

举例：

1. ${\prod }_{name,dept}(Student)$，这里可以看出，属性集并没有写成集合形式，只是用逗号隔开而已，这种写法和集合具有一一对应的关系，不用担心混淆。

这里需要注意，行的提取肯定不会出现重复，但是提取列可能重复。比如仅仅提取一个列，但是这个列的属性只有1种，那最后投影出来的就只有1行。所以投影是会去重的。

本质上，这是因为为每一行都是有唯一键的，但是部分列不一定具有键，所以存在重复可能。

连接

连接是列上的合并+行上的筛选。

条件连接

将满足条件的元组进行拼接。

从这一点看，本质上这就是两个元组的笛卡尔积的子集，这个子集符合我们前面的条件。所以也自然可以转换形式。

写法：

1. $R\underset{A\theta B}{\bowtie }S$。如果碰到重复的属性，我们可以用 关系.属性 来进行区分
2. $R\underset{A\theta B}{\bowtie }S={\sigma }_{A\theta B}(R\times S)$ 即条件连接可以作为笛卡尔积的子集，然后进行一个条件的选择。

举例：

等值连接

$\theta$为=的条件叫做等值连接。

这里就会有个问题，明明都等值了，为什么还要保留相同的两列呢？这里只是为了形式保持一致，符合条件连接定义。后面用自然连接特殊化。

自然连接

自然连接写法不需要加条件，自动合并相同属性组。

自然连接本质上是一种等值连接，但是相比于等值连接来说，进行了重复列删除的操作，提高了简洁性，牺牲了形式一致性。

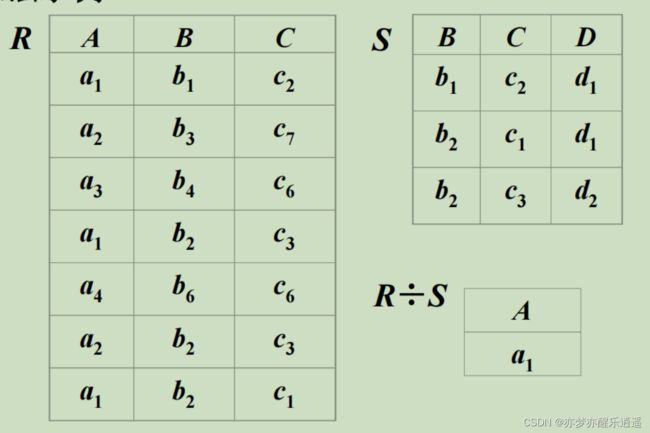
除法

像集

像集是一个属性中元素到另一个属性中元素的映射。

前面的是原象，后面的是像集。

写法：

$Z_{原象值}=\{Z上的像集\}$

举例：

除法

本质上就是，去掉两个关系中相同的属性后剩下的属性。

步骤：

1. 找到相同的属性，假设为A，B
2. 在左边关系中找出每个元素对应的AB上的像集
3. 在右边关系中找出AB的投影
4. 如果左边有某个元素的像集 包含 右边的投影集，那么就保留该元素
5. 这本质上就是一种包含关系，符合 $÷$ 的概念，用左边元素去包含右边整个集合，包含的介质就是左边该元素的像集和右边整个集合的投影，包含就留下来，不包含就舍去。

非常抽象，所以要给足例子：

例1：

例2：

这个例子里包含了实际意义。就是进行一个筛选，筛选是满足像集包含投影的条件的。

扩充的关系运算

属性重命名

就是简单意义上的重命名，即，复制一份并给一个属性重命名或者一组属性重命名。
就是生成一个等价的新关系。

写法：

$$r^{\prime }(R^{\prime })={\delta }_{A\to B}(r)$$

其中，R为原来关系模式，r为原来关系。

用法：

1. 做同一个关系的笛卡尔积。一个关系无法进行，于是复制一份。
2. 做同一个关系的自然连接。同样式单个关系没办法自然连接，链接和没连接一样，重命名后，重命名列不会被消去。

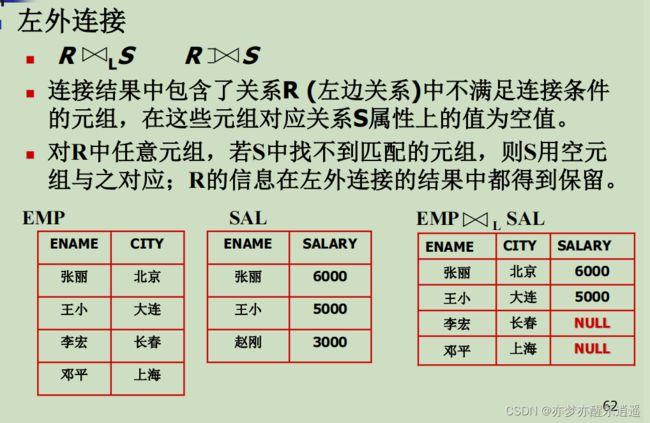
外连接

前面的条件连接，包括自然连接，都会把不满足条件的元组去掉。
对于不满足条件的元组，还可以有另一种处理方法：保留，但是强行合并的部分用NULL区分，由此分出三种保留方法。

1. 左外连接。保留左边不匹配项，右边强行合并用NULL。
2. 右外连接。保留右边不匹配项，左边强行合并有NULL。
3. 完全外连接。保留所有不匹配项，分别用NULL。
   

关系代数应用

用于增删查改

对数据库的各种操作，增删查改，都可以用关系代数表达式来表示。这就是完备性。但是注意，某种操作并不一定只有一种关系表达式，而是可以有各种方法。
当然，一般不直接用关系代数表达式，而是将表达式封装进SQL语言。
这里对关系代数的效果进行理解：

1. 交。
2. 并。一般用于插入。直接∪上一个元组。
3. 差。一般用于删除，取补，取反。
4. 选择。取一些行。
5. 投影。取一些列。
6. 连接。将两个表匹配+合并。通常是使用自然连接，一来是＝关系最常用，二来是能够去重复列，很多时候进行匹配列数不会增加。对于表示联系的关系，可以用
   $S\bowtie SC\bowtie C$，来制造一个直观的表，将多对多转换成一一对应关系。
7. 除。多用于筛选全部的情况。比如筛选选修了所有课程的学生学号。
8. 重命名。
9. 外连接。

案例解析

首先声明一下，S代表学生，C代表课程，SC代表选修关系。

首先用选择筛选学生，然后用投影提取学号和姓名属性。

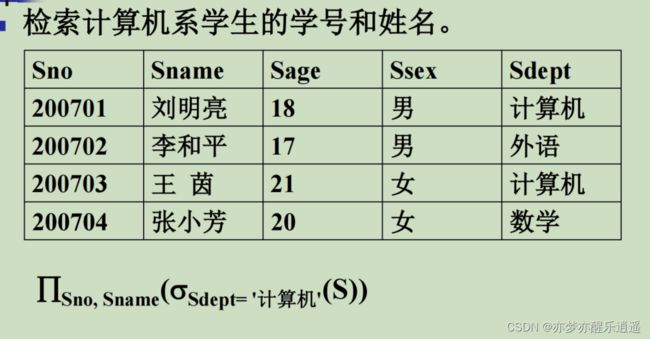
首先将SC中选C1筛选出来，然后进行匹配链接，最后再将学号提取出来。
还有一种方法，先进行匹配连接，然后筛选C1课程，最后将学号提取出来。
至于不选C1的，就用差进行取补运算即可。

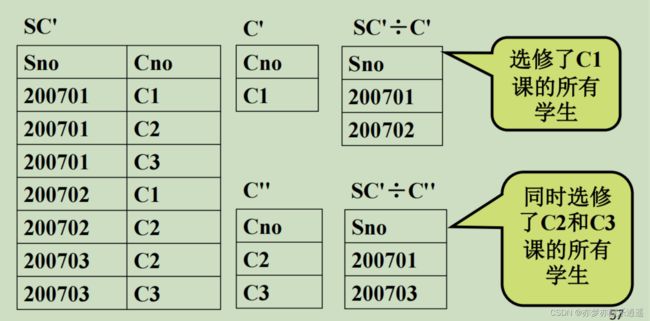
涉及到“全部”二字，自然要用除。为了控制除的相同属性与最后结果，我们需要进行投影。

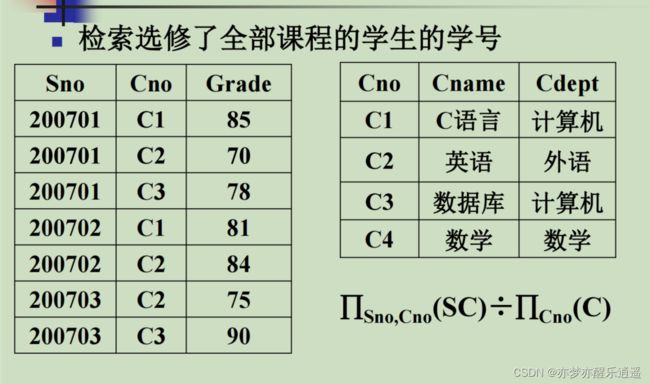
这里从全部变成“至少”。至少两门的情况下，需要建立临时关系，再除。

一般的除，只能剩下一列，那我如果结果要多列怎么办？用除的结果匹配连接一下就好。

第一种方法简单粗暴，直接先将多对多转化为一一对应的选修表，然后将其中Cpno=5的选修找出来，再提取这些学生的名字。这里可能会重复，但刚好投影的特性就是去重。
后面两种方法，运用了很多投影，投影可以将问题简化，只关注对解决问题有效的列。

插入和删除比较简单，插入就并，删除就差，条件判断通过查找来实现。
删除操作中，首先将S和C选择+投影出来简化问题，然后匹配，就可以得出一条元组（这里的选择方式最后只能得出一条元组），然后删去即可。

这个问题的核心在于同一个系。所以首先用重命名复制一份，只保留Sdept（专业）进行匹配，最后的话就会匹配出所有专业相同学生的组合，包括李勇和他自己。然后将和李勇专业相同的匹配筛选出来，这个时候左半边就都是李勇，最后取出右半边的同学。
注意李勇还是会存在，如果不想要，就进行删去。

这个问题可以简化，用除法。这里为什么可以放两个元素在左边，不会吧问题搞复杂吗？是因为Sno和Sname是一一对应的，所以无所谓。在同一个系可以理解为这个学生所在的系包含这个系，自然引出除。
这是除的特殊用法，一个学生只能在一个系中，所包含的系也不可能同时有两种。

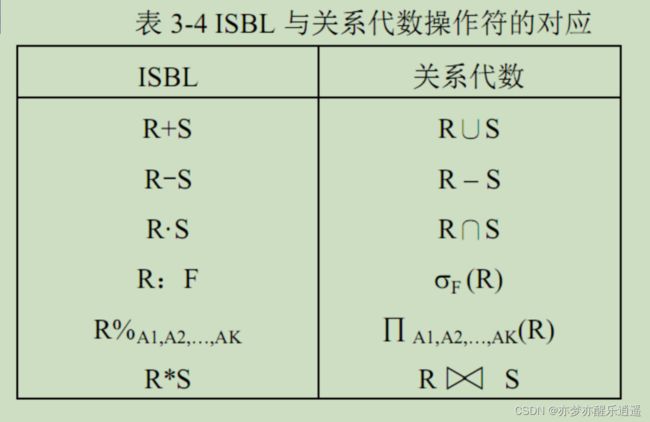
典型关系代数语言：ISBL

这是关系代数的简单抽象，仅仅是将符号编码成计算机内的符号而已。然后属性重命名之类的特殊操作也有对应写法。
这个语言实用性不强，毕竟只是简单抽象的编程语言。

关系演算

比较抽象，通过谓词演算来进行操作，至于具体怎么实现，由系统解决。
这可以说是对关系代数的封装。
所以这个非过程化的，通过关系演算推测背后的实现比较麻烦。

元组关系演算

进行简单观察看出，元组运算对列的选取采用下标方式。S（t）表示t是S中的元组，后面加上t[5]=“计算机”的限制条件。

第二个表达式，首先声明t属于S，然后声明u属于SC，u满足选修C1课且u和t在学生方面匹配

元组关系演算语言：ALPHA

了解即可。

域关系演算

了解即可，核心在于，谓词变元的基本对象是域变量。
域关系演算用于非专业用户，多用于图形界面的表格直接查询。

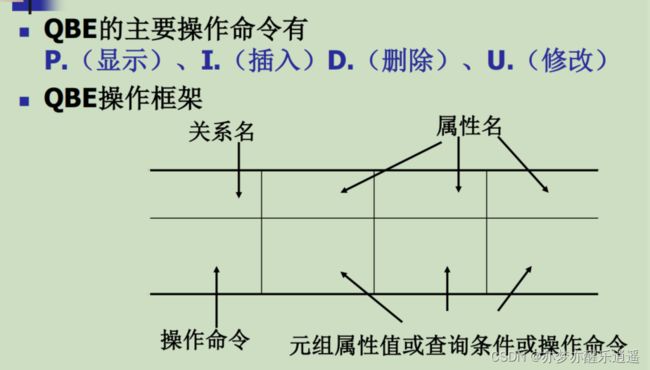
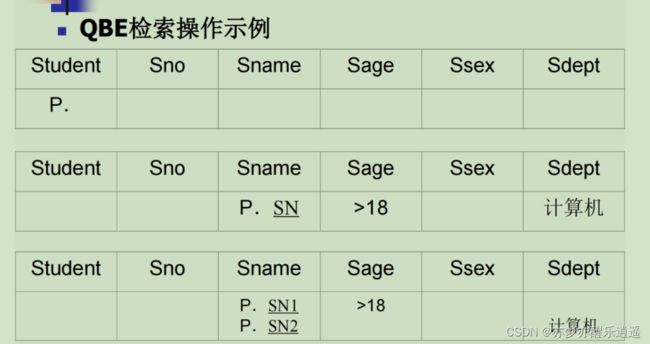
域关系演算语言QBE

关系数据语言

关系数据语言，将关系代数封装，具体的存取路径由DBMS优化机制完成。
而且可以嵌入高级语言中使用，毕竟已经变成高级语言了。
我们现在都用SQL（Structured Query Language）语言，兼顾关系代数和关系演算的双重特性，非过程化·，但是足够结构化。

关系运算的安全性与等价性

这里的安全指的是，不要产生无限的关系，否则会溢出内存。

关系代数运算是安全的，因为本地关系有限，所以只要经过有限次关系代数运算，产生的结果就是有限。

关系演算不一定安全，需要加以限制，定义一个有限的符号集。

确定安全以后，关系代数，元组关系演算，域关系演算三者是可以互相转换的，必然有表达式可以用来替代。

SQL语言（核心）

SQL概述

SQL是现在标准的数据库描述语言。体现出声明式特征，高度非过程化。
综合性强：

1. 数据定义。DDL语言特征
2. 数据操纵。DML语言特征
3. 数据控制。DCL语言特征

可以提供两种使用方式：

1. 交互式SQL。独立，cmd。
2. 嵌入式SQL。嵌入高级程序中，具备过程性。
   

SQL数据定义

SCHEMA定义

如果不指定模式名，默认为用户名。此处体现出用户和SCHEMA的内在联系

TABLE定义

域定义相当于typedef。

constraint是标准约束定义。

强制绑定模式可以用 模式.表命名，或者在模式创建中定义表。

改表可以增删改列。但是新增列是空值，所以不能用NOT NULL

建立索引

索引用于自定义存取路径，加快查询。
通常用B+树实现。B+树就是平衡多路查找树，用于二分查找。

如果不加UNIQUE意味着可能一个索引对应多个数据，但是不推荐在很多重复上建立，没意义.

聚集索引强制储存空间级别的排序。这样，如果要查询15-20之间的数，查到15顺着物理空间找就好了，用不着反复二分查找，对于范围查找有奇效。


索引不会被依赖，所以不用cascade之类的声明

SQL数据操纵——查询

查询是数据库核心技术，本质是对数据操纵对象的选择，是一切操纵的基础。

单表查询

基础，最花的玩法。
基础查：

1. 投影：SELECT选择一些列，可以选择保留重复值。
   列可以是属性，也可以是计算后的值，表达式，聚集函数。
   列还可取别名。
2. 选定数据来源：FROM，这里可以给表取别名。
3. 选择：WHERE加各种条件。比较，与或非，BETWEEN，IN，LIKE（匹配字符串），是否为NULL，EXIST
   选择的各种条件是查询的灵魂。
4. 排序：ORDER BY有两种，ASC（ascending），DESC（descending）
5. 聚集查询：GROUP BY对结果分组，不分组默认全部为一组。
   组内调用聚集函数，聚集函数可以选择是否保留重复值
   算出的组可以用HAVING筛选。注意WHERE作用于元组级别，HAVING作用于组级别。如果同时用，就会先进行WHERE筛选，然后聚集，最后用HAVING筛选
   

连接查询

设计两个以上表的查询，需要连接：

1. 如果不嵌套，直接连接，那么连接几张表，FROM后面就需要放几张表，这代表笛卡尔积。
2. 加上where相当于条件连接。如果再加上AND筛选，相当于连接后再筛选。
3. 如果where是等于，相当于等值连接。
4. 对于特殊的连接，可以将FROM后面的笛卡尔积改成连接声明：
   A NARURAL JOIN B 则产生一个自然连接表
   以此类推，INNER JOIN,LEFT OUTER JOIN ,RIGHT OUTER JOIN,FULL OUTER JOIN
   只不过涉及到内，左右全连接，就要用ON条件而不是where条件，这个比较奇怪。

嵌套查询

嵌套查询可以替代连接查询。其实连接查询会产生比较大的中间结果，所以一般不这么搞。
注意子查询不能用ORDER BY，估计也没人用，没意义。

子查询分两种：

1. 不相关子查询。不依赖于父查询，所以可以一次性查出内层结果，然后外层用内层结果判断即可。
2. 相关子查询。子查询的WHERE要用到父查询的数据，尤其是在比较的时候，这时就得先进行一个父查询，然后丢进子查询查结果，匹配决定父查询是否合格。依次，逐个将父查询全部查完就OK。

注意：

1. 子查询一定要在条件判断的右边。
   

IN类子查询

含义就是父查询的某个属性处于子查询的范围内。
其实很多时候都是等于查询结果，但是IN对这种兼容，等于不也是处于内部吗。

“信息系统”只在C中，所以要与SC关联，再和S关联。关联也很简单，就是IN也可以用链接一步到位，由此可见，嵌套查询多是用于多表查询。可以替代连接操作。

ANY/ALL子查询

any代表存在，而不是任意，all代表所有，这才是任意。
这个可以和统计查询相替代。比如查询比ALL都大，相当于比MAX聚集函数结果大。

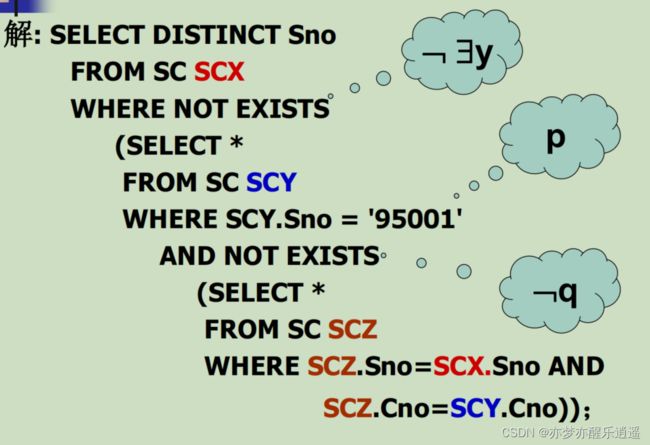
EXIST类子查询

EXIST+select字句可以产生一个布尔值，效率比较高。
相比于IN，他没那么层次分明，习惯于将判断一股脑对到select子句中。
而且还可以组合逻辑谓词，这是难点，但是也可以实现复杂的逻辑。

集合查询

集合查询就是将两个查询块通过交并差形成新结果。
但是集合查询也是可以替代的。

派生表查询

派生表是针对FROM进行优化。
先把数据来源用SELECT字句修改，然后再这个数据里面再进行筛选。
其实前面的自然连接就是这种修改。

SQL数据操纵——增删改

SQL视图

SQL数据控制

嵌入式SQL

查询优化

安全性控制

完整性控制

故障恢复技术

并发控制

数据库设计

理论部分

关系数据库层次重论

前面学的是分成内模式，模式，外模式，但是实际使用中没有这么简单。

首先是关系和关系模式，关系指的是数据本身，关系模式指的是数据的结构定义，比如你的属性列。
关系模式在SQL中用TABLE定义。
基于模式，产生外模式VIEW。

这里会有人问，SCHEMA是什么？SCHEMA将若干个TABLE聚合，相当于命名空间，而SCHEMA一般是和一个数据库用户绑定起来。这也是为什么TABLE默认创建在于用户同名的SCHEMA上。

最终，所有SCHEMA中的所有TABLE构成数据库。

关系模型的存储异常

下面的例子缺点很明显：

1. 数据冗余，本质是信息耦合，可以将一些信息拆出来，这就是后面的模式分解。
2. 插入/删除异常。有一些数据因为被其他列以及约束影响，不能正常插入和删除。
3. 更新异常。因为重复太多，难免出现误差，根本解决办法就是不重复。

以上四点统称为数据存储异常。

根源在于模式设计有问题，没有反映出本质联系，这些本质联系就是数据依赖，所谓的模式优化，就是要发现这些联系，并且做出分解。

数据依赖：

1. 函数依赖，这是最主要的，从1NF到BCNF
2. 多值依赖，从BCNF到4NF
3. 连接依赖，略过。

函数依赖

定义与类型

顾名思义，就是函数映射，可以多对一，但是不可以一对多。

函数依赖分三种：

1. 平凡与非平凡。平凡就是自己依赖自己，这是固有属性。
2. 完全函数依赖和部分函数依赖。部分依赖就是有一些属性是可有可无的，而完全依赖就是缺一不可。
3. 传递函数依赖和直接函数依赖。顾名思义，传递的依赖，而其中有一种特殊的，叫直接函数依赖，这种就是AB互相依赖，实际上是等价关系，所以相当于没传递，直接依赖。

逻辑蕴涵与闭包

函数依赖集F对应一个关系模式R（U，F）

对于F中的某个依赖FD，其被F逻辑蕴涵。只要FD满足R，那么就说F逻辑蕴涵FD。

一般给出的F都不全，所以用F的闭包$F^{+}$ 表示所有逻辑蕴涵的FD集合。

函数依赖公理——Armstrong公理

三条推理规则：

1. 自反。自身可以确定自身，集合本身就具有不重复性，平凡函数，自己顶自己。
2. 增广。用Z将原来的函数特殊化，左右同时增加属性依然成立。XZ推YZ可能是完全依赖XZ也可以推出Y，但是这就是部分依赖了。
3. 传递。不区分XY是否单向，所以最后可能是一一对应，也可能是多对一

三条推论：

1. 合成规则。可以将同一条件得出的两个结论合并。
2. 分解规则。可以将一个结论分解成多个结论。
3. 伪传递规则。
   
   

属性闭包

属性闭包是一个工具，用于导出被蕴含的FD或者判断依赖是否属于F。

对于一个依赖X->Y，如果可以用X导出Y，说明这个依赖被F蕴含。否则就不蕴含。

核心就是，给你一些条件属性，你能通过F导出多少结果。

具体算法如下：

1. 用自己作为初值（自反）之后迭代
2. 每一次迭代，用当前拥有的条件推结果，将结果中新的部分加入条件集
3. 直到不再产生新的结果

这个肯定是有限步，即使每次只得出一个属性，也只需要做U-X+1次即可。

最小依赖集

当两个依赖集可以互相完全导出，那么就是等价的。

在所有等价依赖集中，最小的那个就是最小函数依赖集。有趣的是，这个还不是唯一的，如果计算路径不一样的话。

怎么算就要从最小依赖集特性入手：

1. 右边都是单属性

2. 没有多余的函数依赖。如果一个函数依赖可以被剩余部分导出，说明多余。

3. 左边没有多余属性。

4. 拆分单属性。

5. 去掉多余依赖。逐个去掉，用属性闭包测试是否可以用X推出Y，如果能导出，就多余，注意，如果去掉了，就直接去掉就OK，因为总是等价的，后面可以用新的集合判断。这也就能解释为什么最小依赖不唯一，因为你去掉的顺序不一样。
   3 缩减部分依赖。看看将某个属性缩减后，缩减后依赖是否属于集合。比如将AB变成A或者B，看看能否导出结果，能导出就说明可以缩减，只需要一部分就可以导出结果。

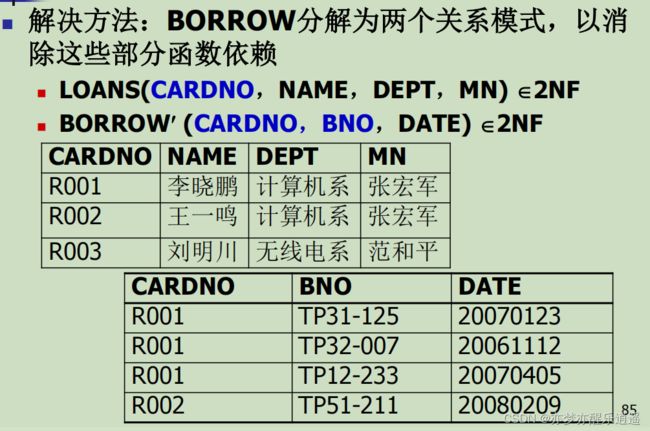
关系模式的规范化——模式分解

关系模式规范化就是将原有模式分解重构成为更加优化的模式。最终目的是要解决数据存储问题。其理论就是各种关系范式。不断规范的过程就是关系范式升级的过程。但是实际上不一定要有多高，关键在于适合。

规范化就是模式分解的过程，模式分解就是将列拆分，重构成为两个新关系。最终目的是减少数据冗余以及提高性能。

模式分解有两个指标：

1. 无损连接分解。分解后的表进行自然连接，结果和原表一样。
2. 保持函数依赖。判断标准用函数依赖集等价判断，但是这个并不一定能保证，实际中有的函数依赖没意义也不需要保持。有的则需要保持来减轻异常。

先给个定义：非候选键部分的属性叫做非主属性。

模式有以下几个等级，逐级加强：

1. 1NF。特征是属性不可分割。这是基本要求
2. 2NF。特征是候选键到非主属性没有冗余属性。做法是将候选键到非主属性的部分函数依赖全部变成完全函数依赖。
3. 3NF。特征是不存在因为传递引起的冗余。做法是将传递函数依赖都去掉。
4. BCNF。特征是候选键内部一一对应，所有依赖都可以用候选键作为起点。做法是将候选键内部的部分依赖去掉。BCNF是函数依赖范畴内的最优结果。
5. 4NF。存在多值依赖时候只能用4NF优化。
6. 进一步还可用连接依赖优化，但是没必要了。

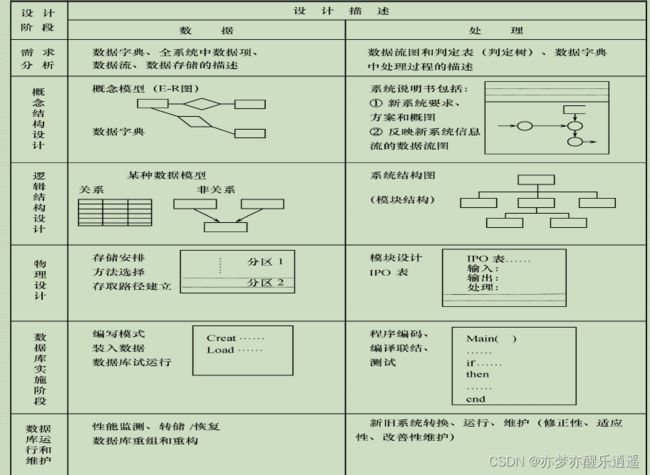
设计流程

数据分析与需求分析——SA方法

这一步最耗时，最困难。在进行前期调差后，对信息进行SA分析，自顶向下，逐层分解。

数据字典是核心结果。

概念模型设计——E-R模型

概念模型通常采用E-R模型。且和具体的DBMS无关。

概念模型通常采用自底向上设计。之后逐步集成。

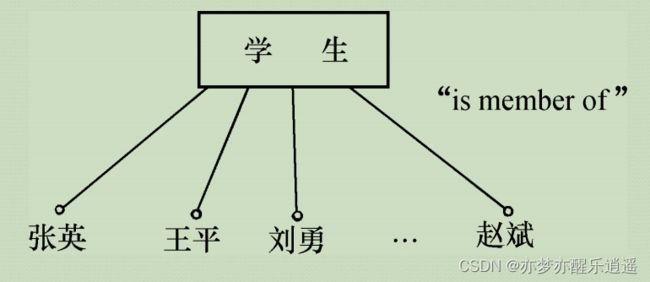
数据抽象与局部视图设计

三种常用抽象：

1. 分类。表示一个实体属于一个实体型。

2. 聚集。表示成分，属性。复杂的聚集，成分还可以是聚集，但是在N1原则中，这个被破除。

3. 概括。超类型和子类型。

设计的原则如下：

大致思路是，找出实体，以及对应的属性，然后规定联系。联系常常是动作，比如所属，包含。

视图集成

合并需要消除冲突：

1. 属性冲突。属性类型，范围，域冲突
2. 命名冲突。属性名字冲突
3. 结构冲突。关系模型冲突，比如列目不同。

合并还需要消除冗余，可以在这一步完成，后面也可以通过规范化来解决。

验证全局概念结构

略。

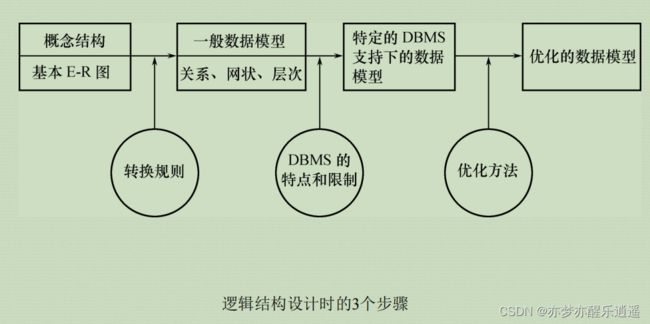
数据模型——逻辑数据库设计

将概念模型转化为数据模型的模式，比如关系数据库对应关系模式。
之后需要进行优化。

转换

对于关系数据库，将实体，属性，联系都转换为关系模式。

实体和属性简单，难点在于联系。

1. 1:1联系和1：n联系。可以独立也可以归并到一端。
2. m：n联系和多方联系。只能单独成关系，单独成关系的键一般是联合键，比如SC中的（sno，cno）

优化

这一步主要通过规范化实现。

1. 确定数据依赖，得出依赖集F。
2. 消除冗余依赖。进行极小化处理。
3. 确定范式。一般是3NF或者BCNF足够了。而且有时候2NF反而更好。根据实际情况来。

还可以通过分解方法实现，这是针对实际应用的优化：

1. 水平分解。将一个关系中的一些元组分出去，这个可能对并发好处。
2. 垂直分解。将属性分开，这个也是看情况。

子模式设计

设计出模式以后，还可以设计外模式。外模式根据用户需求来。

数据模型——物理数据库设计

这一步设计内模式。

选择存取路径

这个相当于模式——内模式映像。

即如何实现SQL语句。

常用存取方法：

1. 索引。主流的是B+树索引。
2. Cluster（聚簇）。
3. HASH

设计关系，索引等数据库文件的物理储存结构

这个涉及到储存的硬件。用性能来评估。

建立数据库与测试维护

数据库投入运行需要逐步测试，

后面维护需要用到重组织，目的是提高系统性能。

1. 重新安排储存位置。
2. 回收垃圾
3. 减少指针链。

可以看到，这些都是和实际的数据打交道，并不会影响到数据模型结构（包括逻辑结构和物理结构）变化。