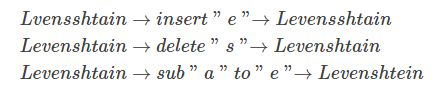知识图谱入门 【六】- 知识融合
知识图谱入门 【一】- 认识图谱技术
知识图谱入门 【二】- 知识表示与知识建模
知识图谱入门 【三】- 知识抽取
知识图谱入门 【四】- 知识挖掘
知识图谱入门 【五】- 知识存储
知识图谱入门 【六】- 知识融合
知识图谱入门 【七】- 知识推理
知识图谱入门 【八】- 语义搜索
知识图谱入门 【九】- 知识问答
知识融合简介
知识融合,即合并两个知识图谱(本体),基本的问题都是研究怎样将来自多个来源的关于同一个实体或概念的描述信息融合起来。需要确认的是:
- 等价实例
- 等价类/子类
- 等价属性/子属性
一个例子如上图所示,图中不同颜色的圆圈代表不同的知识图谱来源,其中在dbpedia.org中的Rome 和geoname.org的roma是同一实体,通过两个sameAs链接。不同知识图谱间的实体对齐是KG融合的主要工作。
除了实体对齐外,还有概念层的知识融合、跨语言的知识融合等工作。
这里值得一提的是,在不同文献中,知识融合有不同的叫法,如本体对齐、本体匹配、Record Linkage、Entity Resolution、实体对齐等叫法,但它们的本质工作是一样的。
知识融合的主要技术挑战为两点:
- 数据质量的挑战: 如命名模糊,数据输入错误、数据丢失、数据格式不一致、缩写等。
- 数据规模的挑战: 数据量大(并行计算)、数据种类多样性、不再仅仅通过名字匹配、多种关系、更多链接等。
知识融合的基本技术流程
知识融合一般分为两步,本体对齐和实体匹配两种的基本流程相似,如下:
数据预处理
数据预处理阶段,原始数据的质量会直接影响到最终链接的结果,不同的数据集对同一实体的描述方式往往是不相同的,对这些数据进行归一化是提高后续链接精确度的重要步骤。
常用的数据预处理有:
- 语法正规化:
- 语法匹配: 如联系电话的表示方法
- 综合属性: 如家庭地址的表达方式
- 数据正规化:
- 移除空格、《》、“”、-等符号
- 输入错误类的拓扑错误
- 用正式名字替换昵称和缩写等
记录连接
假设两个实体的记录x 和y, x和y在第i个属性上的值是xi,yi, 那么通过如下两步进行记录连接:
- 属性相似度: 综合单个属性相似度得到属性相似度向量:
![]()
- 实体相似度: 根据属性相似度向量得到一个实体的相似度。
属性相似度的计算
属性相似度的计算有多种方法,常用的有编辑距离、集合相似度计算、基于向量的相似度计算等。
- 编辑距离: Levenstein、 Wagner and Fisher、 Edit Distance with Afine Gaps
- 集合相似度计算: Jaccard系数, Dice
- 基于向量的相似度计算: Cosine相似度、TFIDF相似度
- ……
编辑距离计算属性相似度
1、Levenshtein Distance
Levenshtein 距离,即最小编辑距离,目的是用最少的编辑操作将一个字符串转换成另一个.举个例子,计算Lvensshtain 与 Levenshtein 间的编辑距离:
上述讲 Lvensshtain转换为Levenshtein ,总共操作3次,编辑距离也就是3。
Levenstein Distance 是典型的动态规划问题,可以通过动态规划算法计算,具体公式如下:
其中, +1 表示的是插入,删除和替换操作的代价。
2、Wagner and Fisher Distance
它是Levenshtein距离的一个扩展,将这个模型中的编辑操作的代价赋予了不同的权重,如下:
![]()
其中del、ins和sub分别是删除、插入和替换的代价。
3、Edit Distance with affine gaps
在上面的两种算法基础上,引入了gap的概念,将上述的插入、删除和替换操作用gap opening 和gap extension代替,编辑操作的代价也就表示为:
![]()
其中s 是open extension的代价, e是extend gap的代价,l是gap的长度。如计算 Lvensshtain 与 Levenshtein间的距离,首先将两个单词首尾对齐,将对应缺少的部分视为gap,如下图中上面和下面单词相比少了第一个e和倒数第三个的e,这是两个gap。下面的单词与上面的比则少了一个s和a,这又是两个gap。加一起一共4个gap,每个长度为1.因此编辑距离为:
![]()
集合相似度计算属性相似度
1、Dice系数
Dice系数用于度量两个集合的相似性,因为可以把字符串理解为一种集合,因此Dice距离也会用于度量字符串的相似性,Dice系数定义如下:
以Lvensshtain 和 Levenshtein为例,两者的相似度为 2 * 9 / (11+11) = 0.82。
2、Jaccard系数
Jaccard 系数适合处理短文本的相似度,定义如下:
可以看出与Dice系数的定义比较相似。两种方法,将文本转换为集合,除了可以用符号分格单词外,还可以考虑用n-gram分割单词,用n-gram分割句子等来构建集合,计算相似度。
3、TF-IDF 基于向量的相似度
TF-IDF主要用来评估某个字或者用某个词对一个文档的重要程度。其中:
举个例子,比如某个语料库中有5万篇文章,含有“健康”的有2万篇,现有一篇文章,共1000个词,‘健康’出现30次,则sim TF-IDF = 30/1000 * log(50000/(20000+1)) = 0.012。
实体相似度的计算
计算实体相似度可从三大方面入手,即聚合、聚类和表示学习。其中:
- 聚合:加权平均、手动制定规则、分类器
- 聚类:层次聚类、相关性聚类、Canopy + K-means
- 表示学习
下面对其进行一一详解。
聚合
加权平均方法,即对相似度得分向量的各个分量进行加权求和,得到最终的实体相似度:
手动制定规则就是给每一个相似度向量的分量设置一个阈值,若超过该阈值则将两实体相连:
对于分类器等机器学习方法,最大的问题是如何生成训练集合,对于此可采用无监督/半监督训练,如EM、生成模型等。或主动学习如众包等方案。
聚类
聚类又可分为层次聚类、相关性聚类、Canopy + K-means等。
1、层次聚类
层次聚类 (Hierarchical Clustering) 通过计算不同类别数据点之间的相似度对在不同的层次的数据进行划分,最终形成树状的聚类结构。
底层的原始数据可以通过相似度函数计算,类之间的相似度有如下三种算法:
- SL(Single Linkage)算法: SL算法又称为最邻近算法 (nearest-neighbor),是用两个类数据点中距离最近的两个数据点间的相似度作为这两个类的距离。
- CL (Complete Linkage)算法: 与SL不同的是取两个类中距离最远的两个点的相似度作为两个类的相似度。
- AL (Average Linkage) 算法: 用两个类中所有点之间相似度的均值作为类间相似度。
举个例子, 有下图的数据,用欧氏距离和SL进行层次聚类。
这样结果就变成:
如此往复就得到最终的分类表:
2、相关性聚类
![]() 表示x,y被分配在同一类中,
表示x,y被分配在同一类中, ![]() 代表x,y是同一类的概率 (x,y之间的相似度),
代表x,y是同一类的概率 (x,y之间的相似度),![]() 和
和![]() 分别是切断x,y之间的边的代价和保留边的代价。相关性聚类的目标就是使用最小的代价找到一个聚类方案。
分别是切断x,y之间的边的代价和保留边的代价。相关性聚类的目标就是使用最小的代价找到一个聚类方案。
![]()
是一个NP-Hard问题,可用贪婪算法近似求解。
3、Canopy + K-means
与K-means不同,Canopy聚类最大的特点是不需要事先指定k值 (即clustering的个数),因此具有很大的实际应用价值,经常将Canopy和K-means配合使用。
用图形表达流程如下图所示:
文字表述为:初始时有一个大的list,其中list中每个点都是一个canopy,设置阈值T1,T2。随机玄奇List中的点P,并计算list中其他的点到点P的距离d,把所有距离d小于T1的点生成Canopy,去除list中d小于T2的点。如此往复这个过程就得到了聚类结果。生成Canopy的过程就像以T2为中心扣下来一块,然后剩下的环就是Canopy。这样一块一块的扣就知道最终list为空。
知识表示学习–知识嵌入
将知识图谱中的实体和关系都映射低维空间向量,直接用数学表达式来计算各个实体之间相似度。这类方法不依赖任何的文本信息,获取到的都是数据的深度特征。
将两个知识图谱映射到同一空间的方法有很多种,它们的桥梁是预连接实体对(训练数据),具体可以看详细论文。
完成映射后如何进行实体链接呢?KG向量训练达到稳定状态之后,对于KG1每一个没有找到链接的实体,在KG2中找到与之距离最近的实体向量进行链接,距离计算方法可采用任何向量之间的距离计算,例如欧式距离或Cosine距离。
分块
分块 (Blocking)是从给定的知识库中的所有实体对中,选出潜在匹配的记录对作为候选项,并将候选项的大小尽可能的缩小。这么做的原因很简单,因为数据太多了。。。我们不可能去一一连接。
常用的分块方法有基于Hash函数的分块、邻近分块等。
首先介绍基于Hash函数的分块。对于记录x,有hash(x)=hihash(x)=hi ,则x映射到与关键字hihi绑定的块CiCi 上。常见的Hash函数有:
- 字符串的前n个字
- n-grams
- 结合多个简单的hash函数等
邻近分块算法包含Canopy聚类、排序邻居算法、Red-Blue Set Cover等。
负载均衡
负载均衡 (Load Balance)来保证所有块中的实体数目相当,从而保证分块对性能的提升程度。最简单的方法是多次Map-Reduce操作。
典型知识融合工具简介
本体对齐-Falcon-AO
Falcon-AO是一个自动的本体匹配系统,已经成为RDF(S)和OWL所表达的Web本体相匹配的一种实用和流行的选择。编程语言为Java。其结构如下图所示:
此处主要介绍它的匹配算法库,其余部分可查看官方文档。
匹配算法库包含V-Doc、I-sub、GMO、PBM四个算法。其中V-Doc即基于虚拟文档的语言学匹配,它是将实体及其周围的实体、名词、文本等信息作一个集合形成虚拟文档的形式。这样我们就可以用TD-IDF等算法进行操作。I-Sub是基于编辑距离的字符串匹配,这个前面我们有详细介绍。可以看出,I-Sub和V-Doc都是基于字符串或文本级别的处理。更进一步的就有了GMO,它是对RDF本体的图结构上做的匹配。PBM则基于分而治之的思想做。
计算相似度的组合策略如下图所示:
首先经由PBM进行分而治之,后进入到V-Doc和 I-Sub ,GMO接收两者的输出做进一步处理,GMO的输出连同V-Doc和I-Sub的输出经由最终的贪心算法进行选取。
Limes 实体匹配
Limes是一个基于度量空间的实体匹配发现框架,适合于大规模数据链接,编程语言是Java。其整体框架如下图所示:
该整体流程用文字表述为:
- 给定源数据集S,目标数据集T,阈值 θθ;
- 样本选取: 从T中选取样本点E来代表T中数据,所谓样本点,也就是能代表距离空间的点。应该在距离空间上均匀分布,各个样本之间距离尽可能大。;
- 过滤: 计算s∈S与e∈E之间的距离m(s, e),利用三角不等式进行过滤;
- 相似度计算: 同上;
- 序列化: 存储为用户指定格式;
三角不等式过滤
给定 (A,m),m是度量标准,相当于相似性函数,A中的点x,y和z相当于三条记录,根据三角不等式有:
![]()
上式通过推理可以得到:
![]()
上式中y相当于样本点。因为样本点E的数量是远小于目标数据集T的数量,所以过滤这一步会急剧减少后续相似性比较的次数,因而对大规模的web数据,这是非常高效的算法。
来自:知识图谱入门 (六) - Pelhans 的博客
http://pelhans.com/2018/04/23/xiaoxiangkg-note6/