Datawhale组队学习-图神经网络（三）

Datawhale组队学习-图神经网络（三）

Taks 03 基于图神经网络的节点表征学习

此次学习分为以下步骤：

• 获取并分析数据集、构建一个方法用于分析节点表征的分布。
• 学习MLP神经网络的理论，观察MLP神经网络用于节点分类的表现，观察基于MLP神经网络学习到的节点表征的分布。
• 学习GCN, GAT这两个图神经网络的理论，对比它们在节点分类任务中的表现以及它们学习到的节点表征的质量。
• 比较MLP，GCN，GAT在节点表征学习能力上的差异。

一、准备工作

获取并分析数据集

from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

dataset = Planetoid(root='dataset', name='Cora', transform=NormalizeFeatures())

print()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

data = dataset[0]  # Get the first graph object.

print()
print(data)
print('======================')

# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}')
print(f'Contains self-loops: {data.contains_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')

我们可以看到：Cora图拥有2,708个节点和10,556条边，平均节点度为3.9，训练集仅使用了140个节点，占整体的5%。我们还可以看到，这个图是无向图，不存在孤立的节点。

数据转换（transform）在将数据输入到神经网络之前修改数据，这一功能可用于实现数据规范化或数据增强。在此例子中，我们使用NormalizeFeatures进行节点特征归一化，使各节点特征总和为1。其他的数据转换方法请参阅torch-geometric-transforms。

可视化节点表征分布的方法

利用TSNE方法将高维的节点表征映射到二维平面空间，然后在二维平面画出节点，来实现节点表征分布的可视化。

二、使用MLP对神经网络进行分类

构造MLP神经网络

import torch
from torch.nn import Linear
import torch.nn.functional as F

class MLP(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(MLP, self).__init__()
        torch.manual_seed(12345)
        self.lin1 = Linear(dataset.num_features, hidden_channels)
        self.lin2 = Linear(hidden_channels, dataset.num_classes)

    def forward(self, x):
        x = self.lin1(x)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.lin2(x)
        return x

model = MLP(hidden_channels=16)
print(model)

我们的MLP由两个线性层、一个ReLU非线性层和一个dropout操作组成。第一个线性层将1433维的节点表征嵌入（embedding）到低维空间中（hidden_channels=16），第二个线性层将节点表征嵌入到类别空间中（num_classes=7）。

MLP神经网络的训练

利用交叉熵损失和Adam优化器来训练这个简单的MLP神经网络。

model = MLP(hidden_channels=16)
criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)  # Define optimizer.

def train():
    model.train()
    optimizer.zero_grad()  # Clear gradients.
    out = model(data.x)  # Perform a single forward pass.
    loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
    loss.backward()  # Derive gradients.
    optimizer.step()  # Update parameters based on gradients.
    return loss
for epoch in range(1, 201):
    loss = train()
    print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')
   

正如我们所看到的，我们的MLP表现相当糟糕，只有大约59%的测试准确性。

**为什么MLP没有表现得更好呢？**其中一个重要原因是，用于训练此神经网络的有标签节点数量过少，此神经网络被过拟合，它对未见过的节点泛化能力很差。

三、卷积图神经网络（GCN）

GCN的定义

GCN 来源于论文“Semi-supervised Classification with Graph Convolutional Network”，其数学定义为，
$${\mathbf{X}}^{\prime }={\hat{\mathbf{D}}}^{-1/2}\hat{\mathbf{A}}{\hat{\mathbf{D}}}^{-1/2}\mathbf{X}\mathbf{\Theta },$$
其中$\hat{\mathbf{A}}=\mathbf{A}+\mathbf{I}$表示插入自环的邻接矩阵（使得每一个节点都有一条边连接到自身），${\hat{D}}_{ii}={\sum }_{j=0}{\hat{A}}_{ij}$表示$\hat{\mathbf{A}}$的对角线度矩阵（对角线元素为对应节点的度，其余元素为0）。邻接矩阵可以包括不为$1$的值，当邻接矩阵不为{0,1}值时，表示邻接矩阵存储的是边的权重。${\hat{\mathbf{D}}}^{-1/2}\hat{\mathbf{A}}{\hat{\mathbf{D}}}^{-1/2}$是对称归一化矩阵，它的节点式表述为：
$${\mathbf{x}}_i^{\prime }=\mathbf{\Theta }\sum _{j\in \mathcal{N}(v)\cup \{i\}}\frac{e_{j,i}}{\sqrt{{\hat{d}}_j{\hat{d}}_i}}{\mathbf{x}}_j$$
其中，${\hat{d}}_i=1+{\sum }_{j\in \mathcal{N}(i)}{e}_{j,i}$，$e_{j,i}$表示从源节点$j$到目标节点$i$的边的对称归一化系数（默认值为1.0）。

PyG中GCNConv 模块说明

GCNConv构造函数接口：

GCNConv(in_channels: int, out_channels: int, improved: bool = False, cached: bool = False, add_self_loops: bool = True, normalize: bool = True, bias: bool = True, **kwargs)

其中：

• in_channels：输入数据维度；
• out_channels：输出数据维度；
• improved：如果为true，$\hat{\mathbf{A}}=\mathbf{A}+2\mathbf{I}$，其目的在于增强中心节点自身信息；
• cached：是否存储${\hat{\mathbf{D}}}^{-1/2}\hat{\mathbf{A}}{\hat{\mathbf{D}}}^{-1/2}$的计算结果以便后续使用，这个参数只应在归纳学习（transductive learning）的场景中设置为true（归纳学习可以简单理解为在训练、验证、测试、推理（inference）四个阶段都只使用一个数据集）；
• add_self_loops：是否在邻接矩阵中增加自环边；
• normalize：是否添加自环边并在运行中计算对称归一化系数；
• bias：是否包含偏置项。

详细内容请大家参阅GCNConv官方文档。

GCN图神经网络的构造

将上面例子中的torch.nn.Linear替换成torch_geometric.nn.GCNConv，我们就可以得到一个GCN图神经网络，如下方代码所示：

from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(GCN, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GCNConv(dataset.num_features, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, dataset.num_classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x

model = GCN(hidden_channels=16)
print(model)

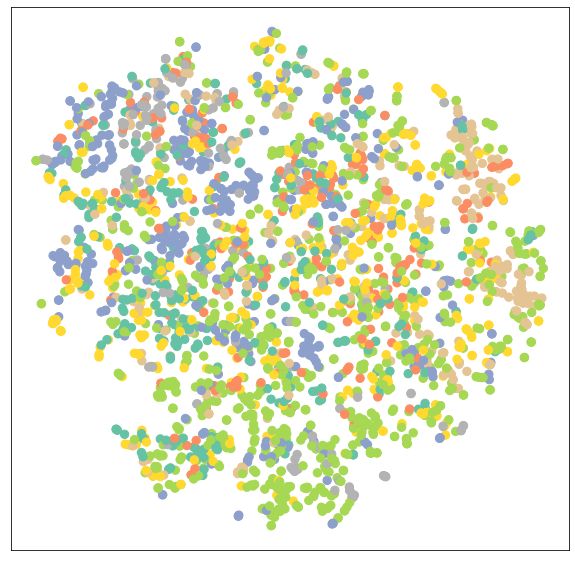
可视化由未经训练的GCN图神经网络生成的节点表征

代码如下所示：

model = GCN(hidden_channels=16)
model.eval()

out = model(data.x, data.edge_index)
visualize(out, color=data.y)

经过visualize函数的处理，7维特征的节点被映射到2维的平面上。

GCN图神经网络的训练

通过下方的代码我们可实现GCN图神经网络的训练：

model = GCN(hidden_channels=16)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()

def train():
      model.train()
      optimizer.zero_grad()  # Clear gradients.
      out = model(data.x, data.edge_index)  # Perform a single forward pass.
      loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
      loss.backward()  # Derive gradients.
      optimizer.step()  # Update parameters based on gradients.
      return loss

for epoch in range(1, 201):
    loss = train()
    print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')

GCN图神经网络的测试

在训练过程结束后，我们检测GCN图神经网络在测试集上的准确性：

def test():
      model.eval()
      out = model(data.x, data.edge_index)
      pred = out.argmax(dim=1)  # Use the class with highest probability.
      test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
      test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
      return test_acc

test_acc = test()
print(f'Test Accuracy: {test_acc:.4f}')

通过简单地将torch.nn.Linear替换成torch_geometric.nn.GCNConv，我们可以取得81.4%的测试准确率！与前面的仅获得59%的测试准确率的MLP图神经网络相比，GCN图神经网络准确性要高得多。这表明节点的邻接信息在取得更好的准确率方面起着关键作用。

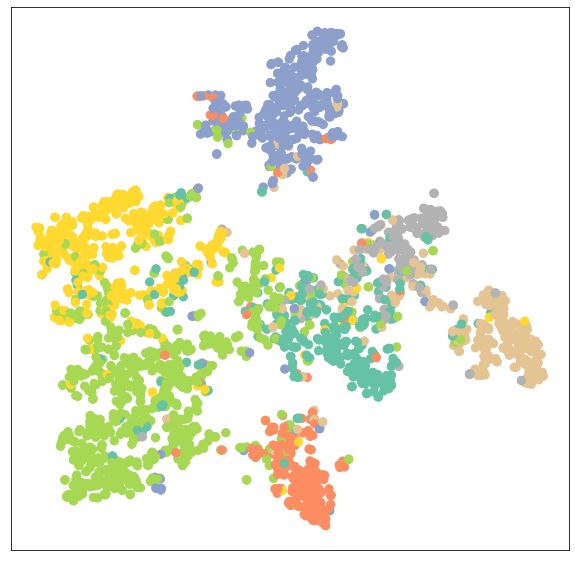
可视化由训练后的GCN图神经网络生成的节点表征

最后我们可视化训练后的GCN图神经网络生成的节点表征，我们会发现“同类节点群聚”的现象更加明显了。这意味着在训练后，GCN图神经网络生成的节点表征质量更高了。

model.eval()

out = model(data.x, data.edge_index)
visualize(out, color=data.y)

四、图注意力神经网络（GAT）

GAT的定义

图注意神经网络（GAT）来源于论文 Graph Attention Networks。其数学定义为，
$${\mathbf{x}}_i^{\prime }={\alpha }_{i,i}\mathbf{\Theta }{\mathbf{x}}_i+\sum _{j\in \mathcal{N}(i)}{\alpha }_{i,j}\mathbf{\Theta }{\mathbf{x}}_j,$$
其中注意力系数${\alpha }_{i,j}$的计算方法为，
$${\alpha }_{i,j}=\frac{\exp \left(\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left({\mathbf{a}}^{\top }[\mathbf{\Theta }{\mathbf{x}}_i\Vert \mathbf{\Theta }{\mathbf{x}}_j]\right)\right)}{{\sum }_{k\in \mathcal{N}(i)\cup \{i\}}\exp \left(\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left({\mathbf{a}}^{\top }[\mathbf{\Theta }{\mathbf{x}}_i\Vert \mathbf{\Theta }{\mathbf{x}}_k]\right)\right)}.$$

PyG中GATConv 模块说明

GATConv构造函数接口：

GATConv(in_channels: Union[int, Tuple[int, int]], out_channels: int, heads: int = 1, concat: bool = True, negative_slope: float = 0.2, dropout: float = 0.0, add_self_loops: bool = True, bias: bool = True, **kwargs)

其中：

• in_channels：输入数据维度；
• out_channels：输出数据维度；
• heads：在GATConv使用多少个注意力模型（Number of multi-head-attentions）；
• concat：如为true，不同注意力模型得到的节点表征被拼接到一起（表征维度翻倍），否则对不同注意力模型得到的节点表征求均值；

详细内容请大家参阅GATConv官方文档

GAT图神经网络的构造

将MLP神经网络例子中的torch.nn.Linear替换成torch_geometric.nn.GATConv，来实现GAT图神经网络的构造，如下方代码所示：

import torch
from torch.nn import Linear
import torch.nn.functional as F

from torch_geometric.nn import GATConv

class GAT(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(GAT, self).__init__()
        torch.manual_seed(12345)
        self.conv1 = GATConv(dataset.num_features, hidden_channels)
        self.conv2 = GATConv(hidden_channels, dataset.num_classes)

    def forward(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.conv2(x, edge_index)
        return x

基于GAT图神经网络的训练和测试，与基于GCN图神经网络的训练和测试相同，此处不再赘述。

结语

在节点表征的学习中，MLP神经网络只考虑了节点自身属性，忽略了节点之间的连接关系，它的结果是最差的；而GCN图神经网络与GAT图神经网络，同时考虑了节点自身信息与周围邻接节点的信息，因此它们的结果都优于MLP神经网络。也就是说，对周围邻接节点的信息的考虑，是图神经网络由于普通深度神经网络的原因。

GCN图神经网络与GAT图神经网络的相同点为：

• 它们都遵循消息传递范式；
• 在邻接节点信息变换阶段，它们都对邻接节点做归一化和线性变换；
• 在邻接节点信息聚合阶段，它们都将变换后的邻接节点信息做求和聚合；
• 在中心节点信息变换阶段，它们都只是简单返回邻接节点信息聚合阶段的聚合结果。

GCN图神经网络与GAT图神经网络的区别在于采取的归一化方法不同：

• 前者根据中心节点与邻接节点的度计算归一化系数，后者根据中心节点与邻接节点的相似度计算归一化系数。
• 前者的归一化方式依赖于图的拓扑结构：不同的节点会有不同的度，同时不同节点的邻接节点的度也不同，于是在一些应用中GCN图神经网络会表现出较差的泛化能力。
• 后者的归一化方式依赖于中心节点与邻接节点的相似度，相似度是训练得到的，因此不受图的拓扑结构的影响，在不同的任务中都会有较好的泛化表现。