数字信号处理 --- 傅氏变换（无公式,无英语）

        傅氏变换是人类对自然界认知的一种方法，是认识事物背后本质的有趣方式，是众多数学分析工具中的一颗璀璨的明星，是所有理工科学生都必不可少的一门课。大家要了解的不仅仅是课本上的复杂公式，更是应该跳出课本，学习傅氏变换的思想，并通过实际项目中的应用去了解她。

 

为什么说傅氏变换是一种正交变换，不同成分（频率）的正弦信号是他的一组正交基？

 

正交

 

        所谓正交，从几何的角度说就是相互垂直，也就是说两者完全相互独立，A不能用B表示，B也不能用A表示。就好像是辣椒炒肉里面的材料，辣椒，肉和盐是一组正交基，因为他们谁也不能代替谁。假设我们改用，辣椒，腌肉和盐来做辣椒炒肉。那么，辣椒，腌肉和盐充其量只能算是一组基，但不正交，因为腌肉里面有盐了。这也正好证明了用一组正交基来表示的好处，因为如果不用腌肉，我按照1:1:1就能完美的重现一盘辣椒炒肉，可以用腌肉来做，我们还要知道腌肉里面究竟有多少盐。

 

基

 

        基就是基本元素的意思，数学上叫基向量。要想完全精确的对一个事物进行分析。基必须完全，该有的一个都不能少，不该有的一个都不能多。用辣椒炒肉来说（辣椒，肉，盐）就是一组基且是正交基。但是这组基做出来的辣椒炒肉可能就不如以（辣椒，肉，盐，味精，葱，姜，蒜）为基做出来的好吃。

要是你用前面那个只有三个元素的基去对一个味道非常好用了其他材料做出来的辣椒炒肉做傅里叶分析（即，傅里叶变换），就无法分辨出其他的调料，食材，以及他们所占的比重。

 

看图说“基”

 

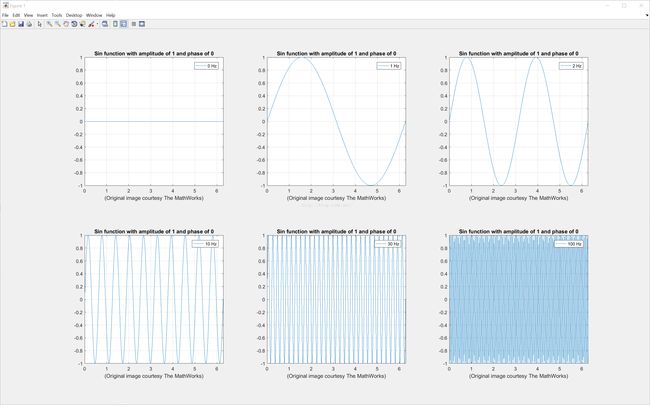
        傅里叶分析的基（基本元素）是用（一定幅度/同一幅度）从0频率到无限大频率的无数多个正弦函数和余弦函数共同组成的。

（点击图像放大）

        上图展示的是一组从0频开始频率不断增大的正弦函数图像。（注意100HZ处图像出现了奇妙的混迭，也就是说信号的高频部分混入了信号的低频部分，信号被破坏了。）

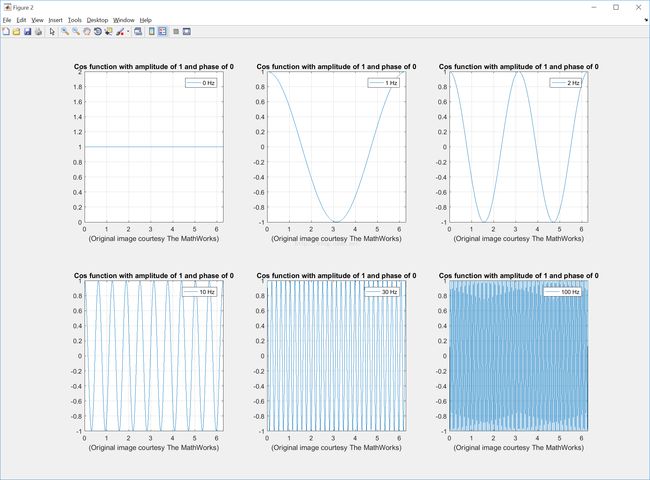
（点击图像放大）

上图展示的是一组从0频开始频率不断增大的余弦函数图像。（同样，100HZ处图像出现了混迭。）

 

大弦嘈嘈如急雨，小弦切切如私语，嘈嘈切切错杂弹，大珠小珠落玉盘

        上图中的一个个信号像不像是一个根根琵琶女手中波动的琴弦？不同粗细的琴弦所发出的从沉闷到尖锐清脆的声音不就是不同频率的正弦信号吗！

        我们的傅里叶分析正是利用了这些无穷无尽的，不同频率的，各个成分所占比重不同的，取之不尽用之不竭的，眼花缭乱的，正弦信号和余弦信号组成的基（基础元素）来张成（构建，编码，分析，编织，合成）自然界中各种各样错综复杂的信号的。

        信号的傅里叶分析或者其他分析就是把一个复杂的问题的简化，分解的方式多重多样参差不齐。其目的是把一个复杂的事物，一个困难的问题，一个费解的现象用不同的方式去再展示，再表达，再深挖，再剖析，以至于我们能够更好地去控制其中的各个成分，增强有用的，去掉或者抑制没用的，去了解事物的一些不同的属性。所以，说白了就是要有“目的”去构建分析和剖析现象的方法方式，变换的方式有很多，但是某些信号或者问题用傅里叶的方式来分析恰到好处（弱水三千只取一瓢，杀鸡焉用宰牛刀说的就是这个道理。）。

 

有很强的目的性/针对性的意义

屠呦呦的青蒿素（屠呦呦变换）和西方的牛痘     

        中华传统中医药学是大自然的宝库，是上帝的馈赠，是劳动人民智慧的结晶。在西方有这么一则故事。18世纪，天花是一种杀伤性很强的疾病。爱得华·詹纳（1749-1823）在伦敦训练以及在军队当了一段外科医生后，成为一个农村医生。他从口头的传说中知道，挤牛奶的少女不会得天花。他相信，挤牛奶的少女只会得很轻的天花和她得无生命危险的牛痘之间会有一定的联系。但他不知道水泡中的脓水保护挤牛奶少女的作用。詹纳相信，用牛痘的液体注入人体内，牛痘的细菌使人能抵抗以后注射的天花细菌所带来的危险。詹纳决定试试他所想出的主意。1796年3月，一位名叫莎拉·内尔姆斯的年轻挤牛奶姑娘去看詹纳。此时詹纳看见莎拉·内尔斯姆正长牛痘，詹纳从她的牛痘肿块中抽出一些液体，后放入詹姆斯手臂上的切割口。詹姆斯是一位农民的儿子，他同意注射内尔姆斯牛痘的液体。注入牛痘后，詹姆斯得病并不利害。六周后，詹姆斯康复。詹纳又给詹姆斯注射病毒，但经过注射牛痘液的詹姆斯不再得天花。詹纳的实验成功了。经过许多进一步成功的试验以后。詹纳在1798年发表他的发现“一个原因的调查和天花疫苗的效果”。詹纳称他的“接种疫苗”想法来自拉丁文牛痘。最后，欧洲的医生都承认，用接种牛痘的方法防止天花的效果很好。接种牛痘遍及欧洲和北美。1980年由于詹纳发现的结果，世卫组织称，全世界的人民已从天花病解放出来。

      

        诺贝尔主题演讲会的主持人，卡罗林斯卡学院传染病学教授 Jan Andersson先生在屠呦呦研究员演讲全程中一直跪在地上，一只手从后面扶着屠教授，另一只手为屠呦呦研究员拿着话筒，30分钟一动未动。

        无独有偶，早在中国古代很早就有医家发现草药青蒿对于疟疾的治疗有极大的帮助。但是仅仅只是知道这种草药能够治疗这种疾病还远不够，其一是青蒿素在青蒿中的含量很低不利于用药，其二不利于定性定量的去分析其中究竟哪个成分的东西在对疾病的治疗起到了至关重要的作用，不能大量生产和人工合成。按照东晋葛洪所著的肘后备急方中所提到了一种分析和提取的方式，屠呦呦利用低沸点的提取方法成功的提取了青蒿中的有效成分青蒿素。她这里所用的提取方法就是一种分析方式，即一种变换，暂且就叫他“屠呦呦变换”吧。其目的性很明确，就是要把青蒿中的各个成分分别分离出来，然后只对有效地分量，成分，系数，基向量，加以抽取，过滤，滤波。这不就是西方对抗天花时所提取的牛痘中的脓水吗。所以从这个角度讲，傅氏变换中的基就是一种滤纸，一种过滤装置，一组滤波器，变换的过程就是过滤，变换后的结果就是每个滤纸过滤出来的东西。注意，傅氏变换所用的滤纸过滤后是没有残渣的，每个成分都会有选择性的通过不同的滤纸来过滤。而屠呦呦的提过过程则会产生残渣，因为它是有选择的。

傅氏分析的周期性以及三个重要元素，幅度，频率，相位。

        傅里叶变换的基础就是用用不同频率的正弦信号来表示（解释）任何信号，所以我想从正弦信号来解释是一个不错的选择。三角函数这一周期性的函数和圆是必不可分的，有些教材中会利用单位圆的概念来定义三角函数。 

        如果把三角函数放在二维笛卡尔坐标系中，假设三角函数是海里有规则的潮汐，他的幅度反映的就是那个无限长大波浪的一个个浪尖的高度。如果把他想象成楼梯，那么针对同一个楼，他的楼梯折返次数越多说明他的频率越高，反之则频率很低。如果想象成一场3000米的赛跑，大家会发现每个运动员都会在不同的起点起跑，这就是相位不同。

现在我们再用圆来解释一遍。

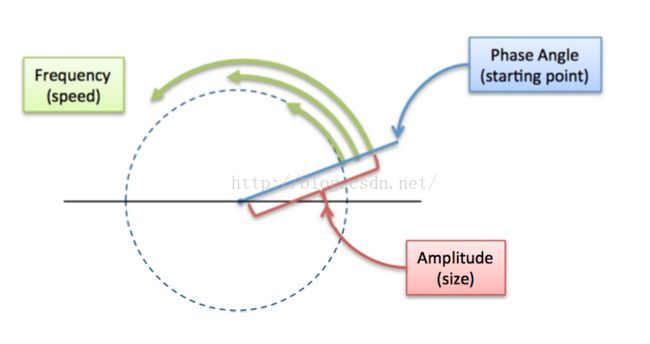
假设现在有个点在做圆周运动。

这个点的旋转速度就是他的频率，例如3圈每秒。

这个点距离远点的距离就是他的幅度，例如1CM。

这个点旋转的起始位置就是他的相位，例如从（1,0）开始。

 

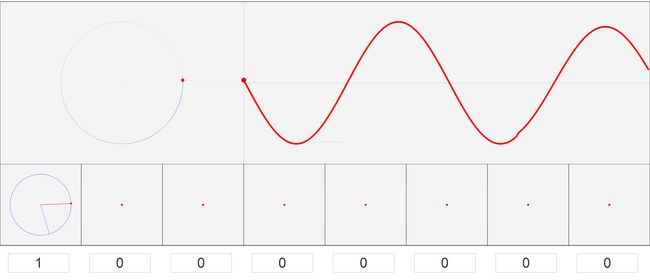
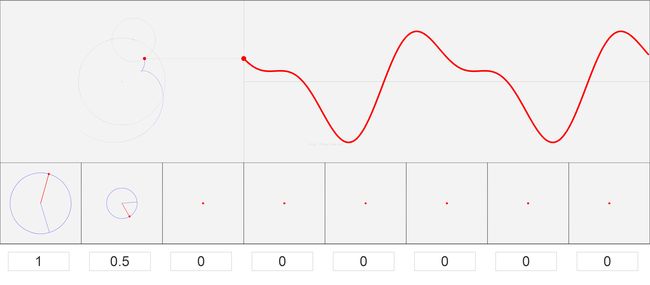
相信大家都能很容易的把三角函数和圆联系起来。下面这个图形能够很好地说明，怎么用不同频率的正弦信号去画圆，去合成不同的信号。

上图为幅度为1，速度（频率）为x，相位在蓝色半径的位置的正弦信号。

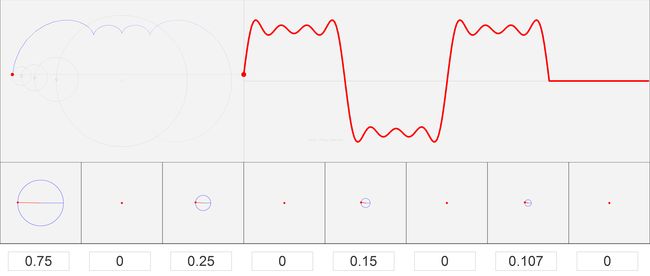
上图为在第一幅图的基础上增加了幅度为0.5，相位和频率都不同的信号。

 

上图为大家很熟悉的方波信号。

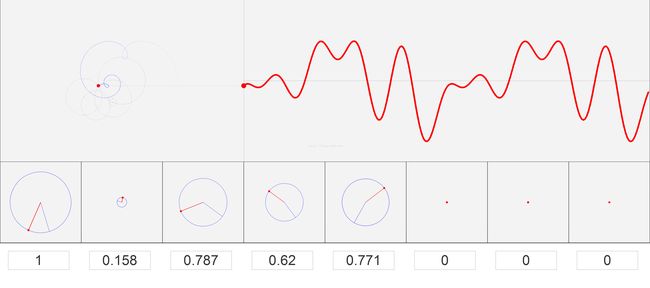
上图为任意信号。

        请牢记，傅里叶变换的基础是用不同频率的三角函数去分析数据，他是周期的，是用周期的砖头去搭建周期的房子。

        为了说明傅里叶变换的基石，即正弦函数。我之所以这么看重正弦函数的性质，是因为它的性质和傅里叶变换的性质息息相关，就好像利用三角形来定义三角函数和利用单位圆来定义三角函数一样，是你中有我，我中有你的。换句话说，要想“充分”了解任何数学变换，必须要了解它的基本构建元素，它的子空间，它的基。恰似，化学之离子，物理之原子，生物之细胞。用横竖撇捺为基构成（张成）的信息（空间）是汉字，用26个字母为基构成的信号（空间）是洋文。

        傅里叶变换只是众多变换中的一种，他的思想很重要。理解了他的想法，你自己也可以去创建自己的分析方式。任何变换都有他的局限性，而且他的局限性就是他的针对性。要学会利用每个变换的属性才能更好地驾驭它，使用它，要知道在什么情况下才能使用它。

望穿秋水----傅里叶分析

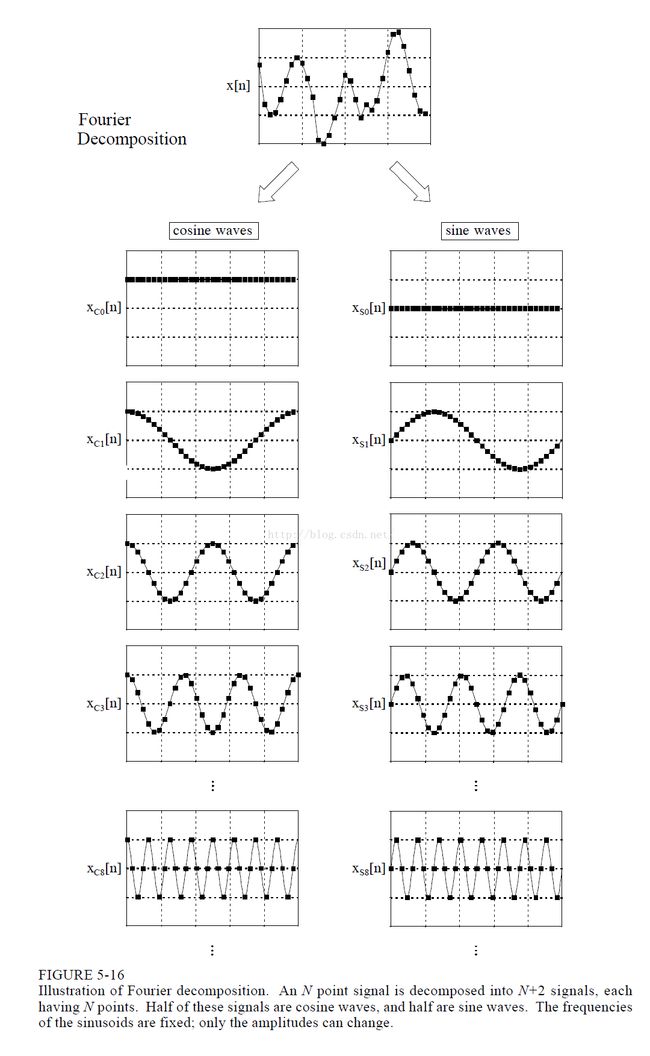
        大家通过之前各种例子的说明，还有傅里叶变换三要素的讲解估计又被搞胡涂了。为了以正视听，还是请大家看看上图对傅里叶分解的解读。N点的信号被分解成N+2个不同的信号，每个信号有N个点，其中一半是由不同频率的余弦信号组成的/表示的，另一半则是由不同频率的正弦信号组成的。这里所有的正弦()和余弦信号()的频率都是固定的，只有他们的幅度可以调整。每一个正弦或者余弦信号的大小反映了这一单一成分在原始信号中所占的比重。

谢谢收看！

（全文完）

对最后一幅傅里叶分解图像的说明做了适当的修改。--- 2022年6月7号

参考文献声明：

1，Steven W. Smith-The Scientist and Engineer's Guide to Digital Signal Processing-California technical Publishing (1999)；

2，MathWorks.

3，http://tech.qq.com/a/20151213/017786.htm

4，http://help.3g.163.com/15/1017/17/B656BKHB00964L9E.html

5，http://toxicdump.org/stuff/FourierToy.swf

《圣经》以弗所书6章3节 ------- 要孝敬父母，使你得福，在世长寿。这是第一条带应许的诫命。

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27​