基于Matlab的Robotics Toolbox工具箱的机器人仿真函数介绍(空间位姿表示与动力学)
文章目录
- 前言
- 一、空间位姿描述
-
- 1. 二维空间
- 2. 三维空间
- 3. 旋转的不同表示方法
-
- 1)欧拉角
- 2)RPY角
- 3)双向量表示
- 4)轴与旋转角
- 5)四元数表示
- 二、动力学
-
- 1. 动力学参数
- 2. 正动力学函数
- 3. 逆运动学函数
- 4. 动力学方程参数
- 总结
前言
![]()
随着我们了解到机器人如何建立运动学模型和动力学模型之后,我们可以使用Matlab中的仿真工具箱内来对模型的准确性进行验证,并且可以通过内置的函数进行简单的轨迹规划和可视化观察,本节涉及到的工具箱是MATLAB自带的Robotics Toolbox工具箱。
一、空间位姿描述
1. 二维空间
平移与旋转函数:
- SE2(x,y,theta):(x,y)的平移 + theta的旋转
T1 = SE2(1,3,30,"deg");
- transl2(x,y):纯(x,y)的平移
T2=trans12(3, 4);
绘制坐标变换:
- trplot2(T):绘制坐标系变换T
trplot2(T1,"frame","1","color","b");
trplot2(T2,"frame","2","color","r");
效果展示:
T1 = SE2(1,3,30,"deg");
trplot2(T1,"frame","1","color","b");
T2=transl2(3, 4);
hold on;
trplot2(T2,"frame","2","color","r");
axis([0 5 2 6]);
2. 三维空间
平移与旋转函数:
- transl(x,y,z):(x,y,z)的平移
R1 = transl(0.5,0.0,0.0);
- trotx(theta) / troty(theta) / trotz(theta):绕x / y / z轴theta的旋转
R2 = trotx(pi/2)*troty(pi/2)*trotz(-pi/2);
- rotx(theta) / roty(theta) / rotz(theta):绕x / y / z轴theta得到的旋转矩阵
R3 = rotx(30,"deg")*roty(30,"deg")*rotz(30,"deg");
注意:trotx和rotx默认都为弧度,trotx可直接与平移函数相乘,而rotx不可
绘制坐标变换:
- trplot ( R ):绘制坐标系变换R
trplot(R1,"frame","A", "color", "b");
trplot(R2,"frame","B", "color", "r");
- tranimate ( R ):绘制旋转动画R
tranimate(R1,"frame","A", "color", "b");
tranimate(R2,"frame","B", "color", "r");
效果展示:
ta = transl(0.5,2.0,1.0)*troty(pi/2)*trotz(-pi/2);
trplot(ta,"frame","A","color","r");
tranimate(ta,"frame","A", "color", "r");
hold on
tb = roty(-pi/2)*rotz(pi/2);
trplot(tb,"frame","B","color","b");
tranimate(tb,"frame","B", "color", "b");
3. 旋转的不同表示方法
1)欧拉角
原理介绍:
- R=rotz(α)*roty(β)*rotz(γ):构造旋转矩阵
R1 = rotz(0.1)*roty(0.2)*rotz(0.3);
- eul=tr2eul( R ):旋转矩阵转换为欧拉角
eul = tr2eul(R);
- R=eul2r(eul):欧拉角转换为旋转矩阵
R = eul2r(0.1,0.2,0.3);
效果展示:
R1 = rotz(0.1)*roty(0.2)*rotz(0.3)
eul = tr2eul(R1)
R2 = eul2r(0.1,0.2,0.3)
2)RPY角
原理介绍:
- R=rotz(α)*roty(β)*rotx(γ):构造旋转矩阵
R1 = rotz(0.3)*roty(0.2)*rotx(0.1);
- rpy=tr2rpy( R ):旋转矩阵转换为RPY角
eul = tr2rpy(R);
- R=rpy2r(α,β,γ,options):RPY角转换为旋转矩阵
R = rpy2r(0.3,0.2,0.1);
效果展示:
R1 = rotz(0.3)*roty(0.2)*rotx(0.1)
eul = tr2rpy(R1)
R2 = rpy2r(0.3,0.2,0.1)
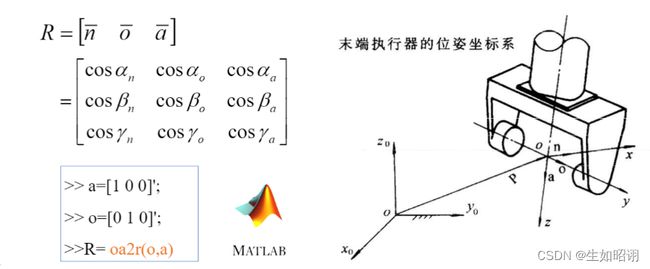
3)双向量表示
原理介绍:
- R=oa2r(o,a):双向量转换为旋转矩阵
a = [1 0 0]';
o = [0 1 0]';
R1 = oa2r(o,a);
效果展示:
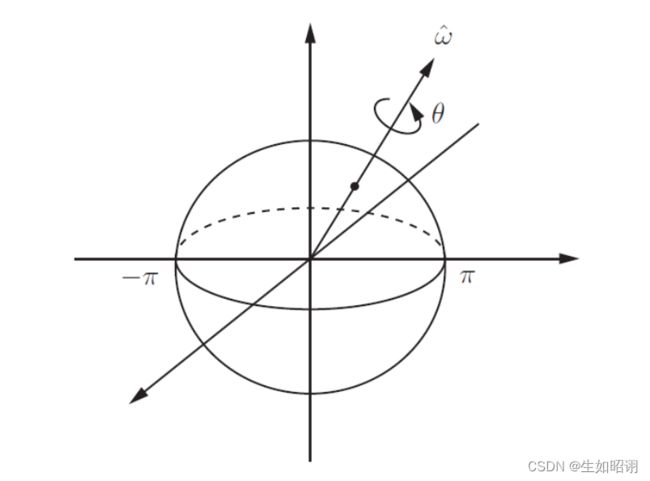
4)轴与旋转角
原理介绍:
函数解释:
- [theta,vec] = tr2angvec( R ):旋转矩阵转换为旋转轴与角
[theta,vec]=tr2angvec( R1 );
- R = angvec2r(theta,vec):旋转轴与角转换为旋转矩阵
R1 = angvec2r(theta,vec);
效果展示:
5)四元数表示
原理介绍:
函数解释:
效果展示:
s=0.95;
v=[0.034, 0.106, 0.143];
Q=UnitQuaternion(s,v); % 组成四元数
q=Q.inv(); % 求共轭
Q.display(); % 打印出四元数
Q.plot(); % 画出出四元数
Q.animate(); % 动画展示四元数
TT=Q.T; % 制作齐次变换矩阵
RR=Q.R; % 制作旋转矩阵
rpy=Q.torpy(); % 转换成rpy角
eul=Q.toeul(); % 转换成eul角
二、动力学
1. 动力学参数
知识介绍:
- 动力学参数:各关节质量、质心位置、惯性张量、惯性矩阵等;
- 获取方法:
- matlab中存在着自带的一些机器人参数,例如puma560等,可直接调用
- 手动创建机器人模型文件(参数可由Solidworks手动测量),保存为.m文件,实例如下:
% mdl_Dyn_5dof.m
% 单臂动力学结构参数
d=[ 0, 0, 0, 0, 0];
a=[ 0, 13, 233.24, 175.64, 0];%/1000
alpha=[ 0, pi/2, 0, 0, pi/2];
%使用offset
L(1)=Link('d',d(1),'a',a(1),'alpha',alpha(1),'modified');
L(2)=Link('d',d(2),'a',a(2),'alpha',alpha(2),'offset',pi/2,'modified');
L(3)=Link('d',d(3),'a',a(3),'alpha',alpha(3),'modified');
L(4)=Link('d',d(4),'a',a(4),'alpha',alpha(4),'offset',pi/2,'modified');
L(5)=Link('d',d(5),'a',a(5),'alpha',alpha(5),'modified');
du=pi/180;
ra=180/pi;
%定义关节范围
L(1).qlim =[-170, 170]*du;
L(2).qlim =[60-70, 60+70]*du;%-10,130
L(3).qlim =[-70-70,-70+70]*du;%-140,0
L(4).qlim =[-70,70]*du;
L(5).qlim =[-170, 170]*du;
bot=SerialLink(L,'name','五自由度机械臂');
%bot.tool= transl(0, 0, tool)
% 动力学参数
data=[
% Ixx, Iyy, Izz, Ixy, Ixz, Iyz, xc, yc, zc, m
47.316, 51.601, 77.113, -0.003, -2.549, -0.016, -0.598, 0.016, -23.413, 0.076;
62.746, 651.130, 704.486, 29.632, -0.001, -0.003, 104.910, -31.512, 0.001, 0.151;
6.264, 224.674, 228.590, -14.345, -0.006, 0, 69.863, 8.061, 0.015, 0.065;
1.502, 1.800, 2.241, 0.455, 0, 0, 4.498, -12.503, 0, 0.008;
13.735, 14.594, 15.321, 0, 0.004, 0, 0.046, 0, 43.571, 0.036
];
% data(:,1:6)=data(:,1:6)./1000000;
% data(:,7:9)=data(:,7:9)./1000;
% 惯性张量
data(:,[5 6])=data(:,[6 5]);%交换Ixz和Iyz
for i=1:5
%I = [L_xx, L_yy, L_zz, L_xy, L_yz, L_xz]
%放入是6个数字,但存储是矩阵形式的9个数字
bot.links(i).I=data(i,1:6);
end
%质心
for i=1:5
bot.links(i).r=data(i,7:9);
end
% 质量
for i=1:5
bot.links(i).m=data(i,10);
end
% 对于空中机械臂,重力与坐标系方向一致,所以为正
% 这与matlab自带的重力系统相反,所以matlab自带函数为负
% 重力单位是m·s-2,也是N/kg,考虑到第二种意义,这里不改变数量值
bot.gravity=[0;0;-9.81];
函数解释:dyn,查看动力学参数
- 查看动力学参数:
mdl_puma560;
p560.dyn;%查看puma560机械臂所有连杆的动力学参数
p560.dyn(2);%查看puma560机械臂第二连杆的动力学参数
p560.links(2).dyn;%查看puma560机械臂第二连杆的动力学参数
2. 正动力学函数
函数解释:fdyn,根据力矩求解关节值
代码示例:
mdl_puma560;
torqfun = [1 2 3 4 5 6];
p560 = p560.nofriction();%为了加快求解速度,选择使用不考虑摩擦的动力学模型
[T,q,qd] = p560.fdyn(1,torqfun);
函数解释:accel,计算角加速度
- qdd = R.accel(q,qd,torqfun):输入位置、速度、力矩求解角加速度
代码示例:
% torqfun = [0,30,6,0,0,0];%设定一组关节力
bot_nf=bot.nofriction();
[T,q,qd] = bot_nf.fdyn(1, torqfun)
for i=1:65,
qdd = bot_nf.accel(q(i,:),qd(i,:),torqfun)
end
3. 逆运动学函数
代码示例:
>> mdl_puma560;
>> A = p560.rne(qn,qz,qz)%当关节角为[0 0.7854 3.1416 0 0.7854 0],关节速度、关节加速度为零,重力加速度为9.81时所需的关节力矩
A =
-0.0000 31.6399 6.0351 0.0000 0.0283 0
4. 动力学方程参数
知识介绍:
函数解释:gravload,求解重力载荷
>> mdl_puma560;
>> p560.gravload([1 2 3 4 5 6])%给定关节角度,求解出重力载荷
ans =
0.0000 -7.9683 8.4581 -0.0197 0.0027 0
函数解释:inertia,求解关节空间惯性矩阵
>> mdl_puma560;
>> p560.inertia([1 2 3 4 5 6])%给定关节角度,求解出关节空间惯性矩阵
ans =
2.6152 -0.6550 -0.0363 0.0001 0.0010 0.0000
-0.6550 4.3038 0.2953 -0.0008 -0.0017 0.0000
-0.0363 0.2953 0.9366 -0.0009 -0.0006 0.0000
0.0001 -0.0008 -0.0009 0.1926 0.0000 0.0000
0.0010 -0.0017 -0.0006 0.0000 0.1713 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.1941
函数解释:coriolis,求解科氏力和向心力的耦合矩阵
>> mdl_puma560;
>> qd = [0.1 0.1 0.1 0.1 0.1 0.1];%给定关节速度
>> C = p560.coriolis(qn,qd)%给定关节角度、关节速度,计算科式力和向心力的耦合矩阵
C =
-0.0267 -0.1291 0.0170 -0.0000 -0.0003 0.0000
0.0627 0.0386 0.0771 -0.0002 -0.0000 -0.0000
-0.0361 -0.0387 -0.0001 -0.0001 -0.0003 -0.0000
0.0000 0.0001 -0.0000 0.0000 0.0000 -0.0000
-0.0000 0.0001 0.0002 -0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0
函数解释:payload,求解有效载荷
>> mdl_puma560;
>> p560.inertia([1 2 3 4 5 6])%没有施加有效载荷时的惯性矩阵
ans =
2.6152 -0.6550 -0.0363 0.0001 0.0010 0.0000
-0.6550 4.3038 0.2953 -0.0008 -0.0017 0.0000
-0.0363 0.2953 0.9366 -0.0009 -0.0006 0.0000
0.0001 -0.0008 -0.0009 0.1926 0.0000 0.0000
0.0010 -0.0017 -0.0006 0.0000 0.1713 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.1941
>> p560.payload(1,[0,0.1,0.2])%施加有效载荷
>> p560.inertia([1 2 3 4 5 6])%施加有效载荷后的惯性矩阵
ans =
2.8033 -0.8506 -0.0951 0.0079 0.0778 0.0368
-0.8506 4.6513 0.4828 -0.0858 -0.1011 -0.0584
-0.0951 0.4828 1.1338 -0.0988 -0.0169 -0.0214
0.0079 -0.0858 -0.0988 0.2416 0.0029 0.0082
0.0778 -0.1011 -0.0169 0.0029 0.2120 0.0192
0.0368 -0.0584 -0.0214 0.0082 0.0192 0.2041
总结
- 声明:本文借鉴了部分博客内容,原文地址奉上:机器人仿真、机械臂动力学、动力学函数解析
本文旨在续接上文,对Matlab的Robotics Toolbox工具箱中有关空间位姿描述,各种旋转矩阵表示方法、动力学相关函数进行整理分析,方便未来查询及寻找解释,后续将会推出一些实际机器人的模型计算,敬请期待