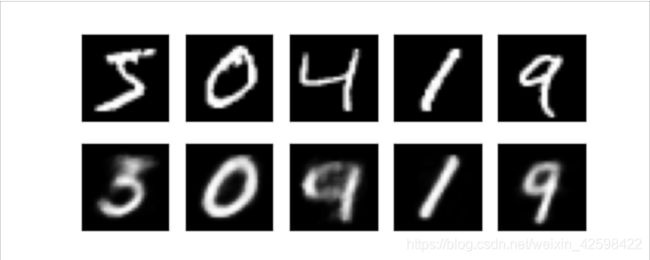莫烦Pytorch入门代码

代码摘自：https://morvanzhou.github.io/tutorials/

1.torch库与numpy库的数据转换

import torch
import numpy as np

# convert numpy to tensor or vise versa
np_data = np.arange(6).reshape((2, 3))
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()
print(
    '\nnumpy array:', np_data,          # [[0 1 2], [3 4 5]]
    '\ntorch tensor:', torch_data,      #  0  1  2 \n 3  4  5    [torch.LongTensor of size 2x3]
    '\ntensor to array:', tensor2array, # [[0 1 2], [3 4 5]]
)
'''
numpy array: [[0 1 2]
 [3 4 5]]
torch tensor: tensor([[0, 1, 2],
        [3, 4, 5]], dtype=torch.int32) 
tensor to array: [[0 1 2]
 [3 4 5]]
'''

# abs
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data)  # 32-bit floating point
print(
    '\nabs',
    '\nnumpy: ', np.abs(data),          # [1 2 1 2]
    '\ntorch: ', torch.abs(tensor)      # [1 2 1 2]
)
'''
abs 
numpy:  [1 2 1 2] 
torch:  tensor([1., 2., 1., 2.])
'''

# sin
print(
    '\nsin',
    '\nnumpy: ', np.sin(data),      # [-0.84147098 -0.90929743  0.84147098  0.90929743]
    '\ntorch: ', torch.sin(tensor)  # [-0.8415 -0.9093  0.8415  0.9093]
)
'''
sin
numpy:  [-0.84147098 -0.90929743  0.84147098  0.90929743]
torch:  tensor([-0.8415, -0.9093,  0.8415,  0.9093])
'''

# mean
print(
    '\nmean',
    '\nnumpy: ', np.mean(data),         # 0.0
    '\ntorch: ', torch.mean(tensor)     # 0.0
)
'''
mean
numpy:  0.0
torch:  tensor(0.)
'''

# matrix multiplication
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data)  # 32-bit floating point
# correct method
print(
    '\nmatrix multiplication (matmul)',
    '\nnumpy: ', np.matmul(data, data),     # [[7, 10], [15, 22]]
    '\ntorch: ', torch.mm(tensor, tensor)   # [[7, 10], [15, 22]]
)
'''
matrix multiplication (matmul)
numpy:  [[ 7 10]
 [15 22]] 
torch:  tensor([[ 7., 10.],
        [15., 22.]])
'''

# incorrect method （错误用法！！！）
data = np.array(data)
print(
    '\nmatrix multiplication (dot)',
    '\nnumpy: ', data.dot(data),        # [[7, 10], [15, 22]]
    '\ntorch: ', tensor.dot(tensor)     # this will convert tensor to [1,2,3,4], you'll get 30.0
)
'''
RuntimeError: 1D tensors expected, got 2D, 2D tensors at ..\aten\src\TH/generic/THTensorEvenMoreMath.cpp:83
'''

2.variable的使用

import torch
from torch.autograd import Variable

# Variable in torch is to build a computational graph,
# but this graph is dynamic compared with a static graph in Tensorflow or Theano.
# So torch does not have placeholder, torch can just pass variable to the computational graph.

tensor = torch.FloatTensor([[1,2],[3,4]])            # build a tensor
variable = Variable(tensor, requires_grad=True)      # build a variable, usually for compute gradients

print(tensor)       # [torch.FloatTensor of size 2x2]
print(variable)     # [torch.FloatTensor of size 2x2]
'''
tensor([[1., 2.],
        [3., 4.]])
tensor([[1., 2.],
        [3., 4.]], requires_grad=True)
'''

# till now the tensor and variable seem the same.
# However, the variable is a part of the graph, it's a part of the auto-gradient.

t_out = torch.mean(tensor*tensor)       # x^2
v_out = torch.mean(variable*variable)   # x^2
print(t_out)
print(v_out)    # 7.5
'''
tensor(7.5000)
tensor(7.5000, grad_fn=)
'''

v_out.backward()    # backpropagation from v_out
# v_out = 1/4 * sum(variable*variable)
# the gradients w.r.t the variable, d(v_out)/d(variable) = 1/4*2*variable = variable/2
print(variable.grad)
'''
tensor([[0.5000, 1.0000],
        [1.5000, 2.0000]])
'''

print(variable)     # this is data in variable format
"""
tensor([[1., 2.],
        [3., 4.]], requires_grad=True)
"""

print(variable.data)    # this is data in tensor format
"""
tensor([[1., 2.],
        [3., 4.]])
"""

print(variable.data.numpy())    # numpy format
"""
[[ 1.  2.]
 [ 3.  4.]]
"""

3.激励函数

import torch
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt

# fake data
x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x = Variable(x)
x_np = x.data.numpy()   # numpy array for plotting

# following are popular activation functions
y_relu = torch.relu(x).data.numpy()
y_sigmoid = torch.sigmoid(x).data.numpy()
y_tanh = torch.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy() # there's no softplus in torch
# y_softmax = torch.softmax(x, dim=0).data.numpy() softmax is a special kind of activation function, it is about probability

# plt to visualize these activation function
plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.subplot(224)
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')

plt.show()

4.回归问题实例

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

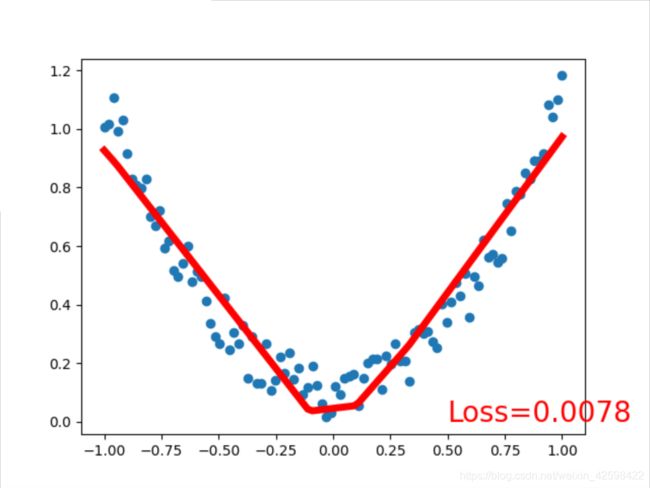
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()

# 定义一个神经网路
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
        self.predict = torch.nn.Linear(n_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)     # define the network
print(net)  # net architecture

optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()  # this is for regression mean squared loss

plt.ion()   # something about plotting

for t in range(200):
    prediction = net(x)     # input x and predict based on x

    loss = loss_func(prediction, y)     # must be (1. nn output, 2. target)

    optimizer.zero_grad()   # clear gradients for next train
    loss.backward()         # backpropagation, compute gradients
    optimizer.step()        # apply gradients

    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()

5.分类问题实例

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
# torch.manual_seed(1)    # reproducible

# make fake data
n_data = torch.ones(100, 2)
x0 = torch.normal(2*n_data, 1)      # class0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100)               # class0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1)     # class1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100)                # class1 y data (tensor), shape=(100, 1)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # shape (200, 2) FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor)    # shape (200,) LongTensor = 64-bit integer

# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
        self.out = torch.nn.Linear(n_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.out(x)
        return x

net = Net(n_feature=2, n_hidden=10, n_output=2)     # define the network
print(net)  # net architecture

optimizer = torch.optim.SGD(net.parameters(), lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()  # the target label is NOT an one-hotted

plt.ion()   # something about plotting

for t in range(100):
    out = net(x)                 # input x and predict based on x
    loss = loss_func(out, y)     # must be (1. nn output, 2. target), the target label is NOT one-hotted

    optimizer.zero_grad()   # clear gradients for next train
    loss.backward()         # backpropagation, compute gradients
    optimizer.step()        # apply gradients

    if t % 2 == 0:
        # plot and show learning process
        plt.cla()
        prediction = torch.max(out, 1)[1]
        pred_y = prediction.data.numpy()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()

6.建立一个神经网络

import torch
import torch.nn.functional as F


# 方式一：replace following class code with an easy sequential network
class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # hidden layer
        self.predict = torch.nn.Linear(n_hidden, n_output)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

net1 = Net(1, 10, 1)

# 方式二：easy and fast way to build your network
net2 = torch.nn.Sequential(
    torch.nn.Linear(1, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 1)
)


print(net1)     # net1 architecture
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

print(net2)     # net2 architecture
"""
Sequential (
  (0): Linear (1 -> 10)
  (1): ReLU ()
  (2): Linear (10 -> 1)
)
"""

7.CNN实现手写数字识别

import os

# third-party library
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 1               # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 50
LR = 0.001              # learning rate
DOWNLOAD_MNIST = False


# Mnist digits dataset
if not(os.path.exists('./mnist/')) or not os.listdir('./mnist/'):
    # not mnist dir or mnist is empyt dir
    DOWNLOAD_MNIST = True

train_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,                                     # this is training data
    transform=torchvision.transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                                                    # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,
)

# plot one example
print(train_data.train_data.size())                 # (60000, 28, 28)
print(train_data.train_labels.size())               # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()

# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

# pick 2000 samples to speed up testing
test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)
test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000]/255.   # shape from (2000, 28, 28) to (2000, 1, 28, 28), value in range(0,1)
test_y = test_data.test_labels[:2000]


class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(         # input shape (1, 28, 28)
            nn.Conv2d(
                in_channels=1,              # input height
                out_channels=16,            # n_filters
                kernel_size=5,              # filter size
                stride=1,                   # filter movement/step
                padding=2,                  # if want same width and length of this image after Conv2d, padding=(kernel_size-1)/2 if stride=1
            ),                              # output shape (16, 28, 28)
            nn.ReLU(),                      # activation
            nn.MaxPool2d(kernel_size=2),    # choose max value in 2x2 area, output shape (16, 14, 14)
        )
        self.conv2 = nn.Sequential(         # input shape (16, 14, 14)
            nn.Conv2d(16, 32, 5, 1, 2),     # output shape (32, 14, 14)
            nn.ReLU(),                      # activation
            nn.MaxPool2d(2),                # output shape (32, 7, 7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)   # fully connected layer, output 10 classes

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)           # flatten the output of conv2 to (batch_size, 32 * 7 * 7)
        output = self.out(x)
        return output, x    # return x for visualization


cnn = CNN()
print(cnn)  # net architecture

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss()                       # the target label is not one-hotted

# following function (plot_with_labels) is for visualization, can be ignored if not interested
from matplotlib import cm
try: from sklearn.manifold import TSNE; HAS_SK = True
except: HAS_SK = False; print('Please install sklearn for layer visualization')
def plot_with_labels(lowDWeights, labels):
    plt.cla()
    X, Y = lowDWeights[:, 0], lowDWeights[:, 1]
    for x, y, s in zip(X, Y, labels):
        c = cm.rainbow(int(255 * s / 9)); plt.text(x, y, s, backgroundcolor=c, fontsize=9)
    plt.xlim(X.min(), X.max()); plt.ylim(Y.min(), Y.max()); plt.title('Visualize last layer'); plt.show(); plt.pause(0.01)

plt.ion()
# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):   # gives batch data, normalize x when iterate train_loader

        output = cnn(b_x)[0]               # cnn output
        loss = loss_func(output, b_y)   # cross entropy loss
        optimizer.zero_grad()           # clear gradients for this training step
        loss.backward()                 # backpropagation, compute gradients
        optimizer.step()                # apply gradients

        if step % 50 == 0:
            test_output, last_layer = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y.data.numpy()).astype(int).sum()) / float(test_y.size(0))
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
            if HAS_SK:
                # Visualization of trained flatten layer (T-SNE)
                tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
                plot_only = 500
                low_dim_embs = tsne.fit_transform(last_layer.data.numpy()[:plot_only, :])
                labels = test_y.numpy()[:plot_only]
                plot_with_labels(low_dim_embs, labels)
plt.ioff()

# print 10 predictions from test data
test_output, _ = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')
'''输出结果：'''
'''
CNN(
  (conv1): Sequential(
    (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (conv2): Sequential(
    (0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (out): Linear(in_features=1568, out_features=10, bias=True)
)
Please install sklearn for layer visualization
Epoch:  0 | train loss: 2.2968 | test accuracy: 0.14
Epoch:  0 | train loss: 0.4375 | test accuracy: 0.83
Epoch:  0 | train loss: 0.6111 | test accuracy: 0.87
Epoch:  0 | train loss: 0.2048 | test accuracy: 0.91
Epoch:  0 | train loss: 0.2585 | test accuracy: 0.93
Epoch:  0 | train loss: 0.0764 | test accuracy: 0.93
Epoch:  0 | train loss: 0.1290 | test accuracy: 0.95
Epoch:  0 | train loss: 0.1609 | test accuracy: 0.96
Epoch:  0 | train loss: 0.0647 | test accuracy: 0.96
Epoch:  0 | train loss: 0.0966 | test accuracy: 0.96
Epoch:  0 | train loss: 0.1824 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0774 | test accuracy: 0.96
Epoch:  0 | train loss: 0.0472 | test accuracy: 0.97
Epoch:  0 | train loss: 0.1196 | test accuracy: 0.97
Epoch:  0 | train loss: 0.1062 | test accuracy: 0.98
Epoch:  0 | train loss: 0.1764 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0414 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0474 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0188 | test accuracy: 0.97
Epoch:  0 | train loss: 0.3208 | test accuracy: 0.97
Epoch:  0 | train loss: 0.0710 | test accuracy: 0.96
Epoch:  0 | train loss: 0.0863 | test accuracy: 0.98
Epoch:  0 | train loss: 0.1158 | test accuracy: 0.96
Epoch:  0 | train loss: 0.0737 | test accuracy: 0.97
[7 2 1 0 4 1 4 9 5 9] prediction number
[7 2 1 0 4 1 4 9 5 9] real number
'''

8.RNN分类实现手写数字识别

import torch
from torch import nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt


# torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 1               # train the training data n times, to save time, we just train 1 epoch
BATCH_SIZE = 64
TIME_STEP = 28          # rnn time step / image height
INPUT_SIZE = 28         # rnn input size / image width
LR = 0.01               # learning rate
DOWNLOAD_MNIST = True   # set to True if haven't download the data


# Mnist digital dataset
train_data = dsets.MNIST(
    root='./mnist/',
    train=True,                         # this is training data
    transform=transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                                        # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,            # download it if you don't have it
)

# plot one example
print(train_data.train_data.size())     # (60000, 28, 28)
print(train_data.train_labels.size())   # (60000)
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[0])
plt.show()

# Data Loader for easy mini-batch return in training
train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

# convert test data into Variable, pick 2000 samples to speed up testing
test_data = dsets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255.   # shape (2000, 28, 28) value in range(0,1)
test_y = test_data.test_labels.numpy()[:2000]    # covert to numpy array


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.LSTM(         # if use nn.RNN(), it hardly learns
            input_size=INPUT_SIZE,
            hidden_size=64,         # rnn hidden unit
            num_layers=1,           # number of rnn layer
            batch_first=True,       # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
        )

        self.out = nn.Linear(64, 10)

    def forward(self, x):
        # x shape (batch, time_step, input_size)
        # r_out shape (batch, time_step, output_size)
        # h_n shape (n_layers, batch, hidden_size)
        # h_c shape (n_layers, batch, hidden_size)
        r_out, (h_n, h_c) = self.rnn(x, None)   # None represents zero initial hidden state

        # choose r_out at the last time step
        out = self.out(r_out[:, -1, :])
        return out


rnn = RNN()
print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.CrossEntropyLoss()                       # the target label is not one-hotted

# training and testing
for epoch in range(EPOCH):
    for step, (b_x, b_y) in enumerate(train_loader):        # gives batch data
        b_x = b_x.view(-1, 28, 28)              # reshape x to (batch, time_step, input_size)

        output = rnn(b_x)                               # rnn output
        loss = loss_func(output, b_y)                   # cross entropy loss
        optimizer.zero_grad()                           # clear gradients for this training step
        loss.backward()                                 # backpropagation, compute gradients
        optimizer.step()                                # apply gradients

        if step % 50 == 0:
            test_output = rnn(test_x)                   # (samples, time_step, input_size)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y).astype(int).sum()) / float(test_y.size)
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)

# print 10 predictions from test data
test_output = rnn(test_x[:10].view(-1, 28, 28))
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10], 'real number')

9.RNN回归实现手写数字识别

import torch
from torch import nn
import numpy as np
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

# Hyper Parameters
TIME_STEP = 10      # rnn time step
INPUT_SIZE = 1      # rnn input size
LR = 0.02           # learning rate

# show data
steps = np.linspace(0, np.pi*2, 100, dtype=np.float32)  # float32 for converting torch FloatTensor
x_np = np.sin(steps)
y_np = np.cos(steps)
plt.plot(steps, y_np, 'r-', label='target (cos)')
plt.plot(steps, x_np, 'b-', label='input (sin)')
plt.legend(loc='best')
plt.show()


class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.RNN(
            input_size=INPUT_SIZE,
            hidden_size=32,     # rnn hidden unit
            num_layers=1,       # number of rnn layer
            batch_first=True,   # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h_state):
        # x (batch, time_step, input_size)
        # h_state (n_layers, batch, hidden_size)
        # r_out (batch, time_step, hidden_size)
        r_out, h_state = self.rnn(x, h_state)

        outs = []    # save all predictions
        for time_step in range(r_out.size(1)):    # calculate output for each time step
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state

        # instead, for simplicity, you can replace above codes by follows
        # r_out = r_out.view(-1, 32)
        # outs = self.out(r_out)
        # outs = outs.view(-1, TIME_STEP, 1)
        # return outs, h_state
        
        # or even simpler, since nn.Linear can accept inputs of any dimension 
        # and returns outputs with same dimension except for the last
        # outs = self.out(r_out)
        # return outs

rnn = RNN()
print(rnn)

optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
loss_func = nn.MSELoss()

h_state = None      # for initial hidden state

plt.figure(1, figsize=(12, 5))
plt.ion()           # continuously plot

for step in range(100):
    start, end = step * np.pi, (step+1)*np.pi   # time range
    # use sin predicts cos
    steps = np.linspace(start, end, TIME_STEP, dtype=np.float32, endpoint=False)  # float32 for converting torch FloatTensor
    x_np = np.sin(steps)
    y_np = np.cos(steps)

    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])    # shape (batch, time_step, input_size)
    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])

    prediction, h_state = rnn(x, h_state)   # rnn output
    # !! next step is important !!
    h_state = h_state.data        # repack the hidden state, break the connection from last iteration

    loss = loss_func(prediction, y)         # calculate loss
    optimizer.zero_grad()                   # clear gradients for this training step
    loss.backward()                         # backpropagation, compute gradients
    optimizer.step()                        # apply gradients

    # plotting
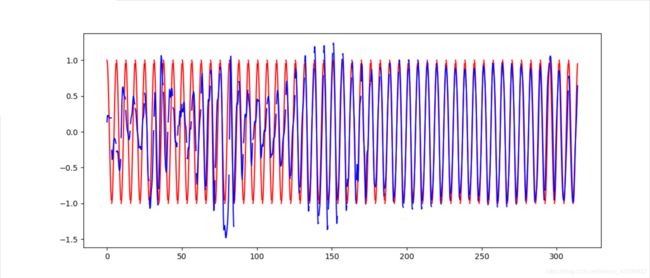
    plt.plot(steps, y_np.flatten(), 'r-')
    plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
    plt.draw(); plt.pause(0.05)

plt.ioff()
plt.show()

'''
RNN(
  (rnn): RNN(1, 32, batch_first=True)
  (out): Linear(in_features=32, out_features=1, bias=True)
)
'''

训练结果：

9.自动编码器

import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy as np


# torch.manual_seed(1)    # reproducible

# Hyper Parameters
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005         # learning rate
DOWNLOAD_MNIST = True
N_TEST_IMG = 5

# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
    root='./mnist/',
    train=True,                                     # this is training data
    transform=torchvision.transforms.ToTensor(),    # Converts a PIL.Image or numpy.ndarray to
                                                    # torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
    download=DOWNLOAD_MNIST,                        # download it if you don't have it
)

# plot one example
print(train_data.train_data.size())     # (60000, 28, 28)
print(train_data.train_labels.size())   # (60000)
plt.imshow(train_data.train_data[2].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[2])
plt.show()

# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)


class AutoEncoder(nn.Module):
    def __init__(self):
        super(AutoEncoder, self).__init__()

        self.encoder = nn.Sequential(
            nn.Linear(28*28, 128),
            nn.Tanh(),
            nn.Linear(128, 64),
            nn.Tanh(),
            nn.Linear(64, 12),
            nn.Tanh(),
            nn.Linear(12, 3),   # compress to 3 features which can be visualized in plt
        )
        self.decoder = nn.Sequential(
            nn.Linear(3, 12),
            nn.Tanh(),
            nn.Linear(12, 64),
            nn.Tanh(),
            nn.Linear(64, 128),
            nn.Tanh(),
            nn.Linear(128, 28*28),
            nn.Sigmoid(),       # compress to a range (0, 1)
        )

    def forward(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return encoded, decoded


autoencoder = AutoEncoder()

optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()

# initialize figure
f, a = plt.subplots(2, N_TEST_IMG, figsize=(5, 2))
plt.ion()   # continuously plot

# original data (first row) for viewing
view_data = train_data.train_data[:N_TEST_IMG].view(-1, 28*28).type(torch.FloatTensor)/255.
for i in range(N_TEST_IMG):
    a[0][i].imshow(np.reshape(view_data.data.numpy()[i], (28, 28)), cmap='gray'); a[0][i].set_xticks(()); a[0][i].set_yticks(())

for epoch in range(EPOCH):
    for step, (x, b_label) in enumerate(train_loader):
        b_x = x.view(-1, 28*28)   # batch x, shape (batch, 28*28)
        b_y = x.view(-1, 28*28)   # batch y, shape (batch, 28*28)

        encoded, decoded = autoencoder(b_x)

        loss = loss_func(decoded, b_y)      # mean square error
        optimizer.zero_grad()               # clear gradients for this training step
        loss.backward()                     # backpropagation, compute gradients
        optimizer.step()                    # apply gradients

        if step % 100 == 0:
            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy())

            # plotting decoded image (second row)
            _, decoded_data = autoencoder(view_data)
            for i in range(N_TEST_IMG):
                a[1][i].clear()
                a[1][i].imshow(np.reshape(decoded_data.data.numpy()[i], (28, 28)), cmap='gray')
                a[1][i].set_xticks(()); a[1][i].set_yticks(())
            plt.draw(); plt.pause(0.05)

plt.ioff()
plt.show()

# visualize in 3D plot
view_data = train_data.train_data[:200].view(-1, 28*28).type(torch.FloatTensor)/255.
encoded_data, _ = autoencoder(view_data)
fig = plt.figure(2); ax = Axes3D(fig)
X, Y, Z = encoded_data.data[:, 0].numpy(), encoded_data.data[:, 1].numpy(), encoded_data.data[:, 2].numpy()
values = train_data.train_labels[:200].numpy()
for x, y, z, s in zip(X, Y, Z, values):
    c = cm.rainbow(int(255*s/9)); ax.text(x, y, z, s, backgroundcolor=c)
ax.set_xlim(X.min(), X.max()); ax.set_ylim(Y.min(), Y.max()); ax.set_zlim(Z.min(), Z.max())
plt.show()

10.强化学习

"""
Dependencies:
torch: 0.4
gym: 0.8.1
numpy
"""
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import gym

# Hyper Parameters
BATCH_SIZE = 32
LR = 0.01                   # learning rate
EPSILON = 0.9               # greedy policy
GAMMA = 0.9                 # reward discount
TARGET_REPLACE_ITER = 100   # target update frequency
MEMORY_CAPACITY = 2000
env = gym.make('CartPole-v0')
env = env.unwrapped
N_ACTIONS = env.action_space.n
N_STATES = env.observation_space.shape[0]
ENV_A_SHAPE = 0 if isinstance(env.action_space.sample(), int) else env.action_space.sample().shape     # to confirm the shape


class Net(nn.Module):
    def __init__(self, ):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(N_STATES, 50)
        self.fc1.weight.data.normal_(0, 0.1)   # initialization
        self.out = nn.Linear(50, N_ACTIONS)
        self.out.weight.data.normal_(0, 0.1)   # initialization

    def forward(self, x):
        x = self.fc1(x)
        x = F.relu(x)
        actions_value = self.out(x)
        return actions_value


class DQN(object):
    def __init__(self):
        self.eval_net, self.target_net = Net(), Net()

        self.learn_step_counter = 0                                     # for target updating
        self.memory_counter = 0                                         # for storing memory
        self.memory = np.zeros((MEMORY_CAPACITY, N_STATES * 2 + 2))     # initialize memory
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
        self.loss_func = nn.MSELoss()

    def choose_action(self, x):
        x = torch.unsqueeze(torch.FloatTensor(x), 0)
        # input only one sample
        if np.random.uniform() < EPSILON:   # greedy
            actions_value = self.eval_net.forward(x)
            action = torch.max(actions_value, 1)[1].data.numpy()
            action = action[0] if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)  # return the argmax index
        else:   # random
            action = np.random.randint(0, N_ACTIONS)
            action = action if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)
        return action

    def store_transition(self, s, a, r, s_):
        transition = np.hstack((s, [a, r], s_))
        # replace the old memory with new memory
        index = self.memory_counter % MEMORY_CAPACITY
        self.memory[index, :] = transition
        self.memory_counter += 1

    def learn(self):
        # target parameter update
        if self.learn_step_counter % TARGET_REPLACE_ITER == 0:
            self.target_net.load_state_dict(self.eval_net.state_dict())
        self.learn_step_counter += 1

        # sample batch transitions
        sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE)
        b_memory = self.memory[sample_index, :]
        b_s = torch.FloatTensor(b_memory[:, :N_STATES])
        b_a = torch.LongTensor(b_memory[:, N_STATES:N_STATES+1].astype(int))
        b_r = torch.FloatTensor(b_memory[:, N_STATES+1:N_STATES+2])
        b_s_ = torch.FloatTensor(b_memory[:, -N_STATES:])

        # q_eval w.r.t the action in experience
        q_eval = self.eval_net(b_s).gather(1, b_a)  # shape (batch, 1)
        q_next = self.target_net(b_s_).detach()     # detach from graph, don't backpropagate
        q_target = b_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1)   # shape (batch, 1)
        loss = self.loss_func(q_eval, q_target)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

dqn = DQN()

print('\nCollecting experience...')
for i_episode in range(400):
    s = env.reset()
    ep_r = 0
    while True:
        env.render()
        a = dqn.choose_action(s)

        # take action
        s_, r, done, info = env.step(a)

        # modify the reward
        x, x_dot, theta, theta_dot = s_
        r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
        r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
        r = r1 + r2

        dqn.store_transition(s, a, r, s_)

        ep_r += r
        if dqn.memory_counter > MEMORY_CAPACITY:
            dqn.learn()
            if done:
                print('Ep: ', i_episode,
                      '| Ep_r: ', round(ep_r, 2))

        if done:
            break
        s = s_
'''
Collecting experience...
Ep:  199 | Ep_r:  1.31
Ep:  200 | Ep_r:  2.17
Ep:  201 | Ep_r:  3.72
Ep:  202 | Ep_r:  2.78
Ep:  203 | Ep_r:  1.89
Ep:  204 | Ep_r:  2.4
Ep:  205 | Ep_r:  0.73
Ep:  206 | Ep_r:  1.53
Ep:  207 | Ep_r:  2.21
Ep:  208 | Ep_r:  1.46
Ep:  209 | Ep_r:  2.28
Ep:  210 | Ep_r:  4.85
Ep:  211 | Ep_r:  1.74
Ep:  212 | Ep_r:  7.58
Ep:  213 | Ep_r:  1.7
Ep:  214 | Ep_r:  3.4
Ep:  215 | Ep_r:  3.12
Ep:  216 | Ep_r:  2.25
Ep:  217 | Ep_r:  2.35
Ep:  218 | Ep_r:  3.22
Ep:  219 | Ep_r:  5.32
Ep:  220 | Ep_r:  6.1
Ep:  221 | Ep_r:  2.33
Ep:  222 | Ep_r:  8.15
Ep:  223 | Ep_r:  3.26
Ep:  224 | Ep_r:  1.4
Ep:  225 | Ep_r:  4.28
Ep:  226 | Ep_r:  3.43
Ep:  227 | Ep_r:  1.13
Ep:  228 | Ep_r:  2.94
Ep:  229 | Ep_r:  1.83
Ep:  230 | Ep_r:  21.3
Ep:  231 | Ep_r:  2.79
Ep:  232 | Ep_r:  21.15
Ep:  233 | Ep_r:  10.14
Ep:  234 | Ep_r:  9.51
Ep:  235 | Ep_r:  2.37
Ep:  236 | Ep_r:  15.11
Ep:  237 | Ep_r:  42.06
Ep:  238 | Ep_r:  39.99
Ep:  239 | Ep_r:  52.94
Ep:  240 | Ep_r:  86.02
Ep:  241 | Ep_r:  31.62
Ep:  242 | Ep_r:  124.85
'''

11.GAN网络

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible
# np.random.seed(1)

# Hyper Parameters
BATCH_SIZE = 64
LR_G = 0.0001           # learning rate for generator
LR_D = 0.0001           # learning rate for discriminator
N_IDEAS = 5             # think of this as number of ideas for generating an art work (Generator)
ART_COMPONENTS = 15     # it could be total point G can draw in the canvas
PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)])

# show our beautiful painting range
# plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
# plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
# plt.legend(loc='upper right')
# plt.show()


def artist_works():     # painting from the famous artist (real target)
    a = np.random.uniform(1, 2, size=BATCH_SIZE)[:, np.newaxis]
    paintings = a * np.power(PAINT_POINTS, 2) + (a-1)
    paintings = torch.from_numpy(paintings).float()
    return paintings

G = nn.Sequential(                      # Generator
    nn.Linear(N_IDEAS, 128),            # random ideas (could from normal distribution)
    nn.ReLU(),
    nn.Linear(128, ART_COMPONENTS),     # making a painting from these random ideas
)

D = nn.Sequential(                      # Discriminator
    nn.Linear(ART_COMPONENTS, 128),     # receive art work either from the famous artist or a newbie like G
    nn.ReLU(),
    nn.Linear(128, 1),
    nn.Sigmoid(),                       # tell the probability that the art work is made by artist
)

opt_D = torch.optim.Adam(D.parameters(), lr=LR_D)
opt_G = torch.optim.Adam(G.parameters(), lr=LR_G)

plt.ion()   # something about continuous plotting

for step in range(10000):
    artist_paintings = artist_works()  # real painting from artist
    G_ideas = torch.randn(BATCH_SIZE, N_IDEAS, requires_grad=True)  # random ideas\n
    G_paintings = G(G_ideas)                    # fake painting from G (random ideas)
    prob_artist1 = D(G_paintings)               # D try to reduce this prob
    G_loss = torch.mean(torch.log(1. - prob_artist1))  
    opt_G.zero_grad()
    G_loss.backward()
    opt_G.step()
     
    prob_artist0 = D(artist_paintings)          # D try to increase this prob
    prob_artist1 = D(G_paintings.detach())  # D try to reduce this prob
    D_loss = - torch.mean(torch.log(prob_artist0) + torch.log(1. - prob_artist1))
    opt_D.zero_grad()
    D_loss.backward(retain_graph=True)      # reusing computational graph
    opt_D.step()

    if step % 50 == 0:  # plotting
        plt.cla()
        plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0], c='#4AD631', lw=3, label='Generated painting',)
        plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
        plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
        plt.text(-.5, 2.3, 'D accuracy=%.2f (0.5 for D to converge)' % prob_artist0.data.numpy().mean(), fontdict={'size': 13})
        plt.text(-.5, 2, 'D score= %.2f (-1.38 for G to converge)' % -D_loss.data.numpy(), fontdict={'size': 13})
        plt.ylim((0, 3));plt.legend(loc='upper right', fontsize=10);plt.draw();plt.pause(0.01)

plt.ioff()
plt.show()

GAN网络生成的绿线始终处在蓝线与红线之间。

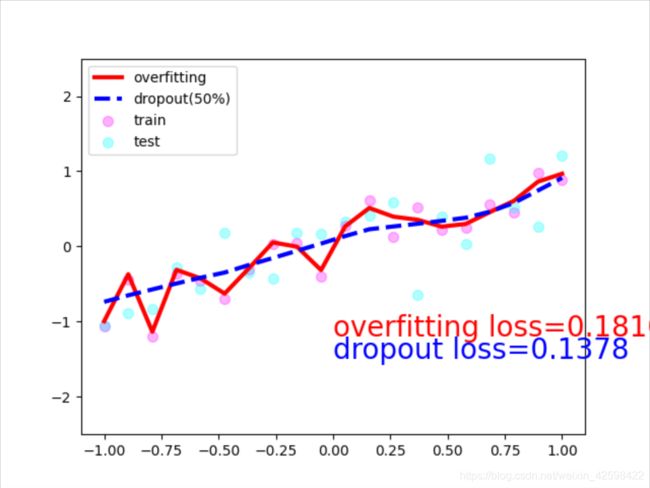
12.dropout防止过拟合

import torch
import matplotlib.pyplot as plt

# torch.manual_seed(1)    # reproducible

N_SAMPLES = 20
N_HIDDEN = 300

# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))

# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()

net_overfitting = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

net_dropped = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

print(net_overfitting)  # net architecture
print(net_dropped)

optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()

plt.ion()   # something about plotting

for t in range(500):
    pred_ofit = net_overfitting(x)
    pred_drop = net_dropped(x)
    loss_ofit = loss_func(pred_ofit, y)
    loss_drop = loss_func(pred_drop, y)

    optimizer_ofit.zero_grad()
    optimizer_drop.zero_grad()
    loss_ofit.backward()
    loss_drop.backward()
    optimizer_ofit.step()
    optimizer_drop.step()

    if t % 10 == 0:
        # change to eval mode in order to fix drop out effect
        net_overfitting.eval()
        net_dropped.eval()  # parameters for dropout differ from train mode

        # plotting
        plt.cla()
        test_pred_ofit = net_overfitting(test_x)
        test_pred_drop = net_dropped(test_x)
        plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='overfitting')
        plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')
        plt.text(0, -1.2, 'overfitting loss=%.4f' % loss_func(test_pred_ofit, test_y).data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.text(0, -1.5, 'dropout loss=%.4f' % loss_func(test_pred_drop, test_y).data.numpy(), fontdict={'size': 20, 'color': 'blue'})
        plt.legend(loc='upper left'); plt.ylim((-2.5, 2.5));plt.pause(0.1)

        # change back to train mode
        net_overfitting.train()
        net_dropped.train()

plt.ioff()
plt.show()

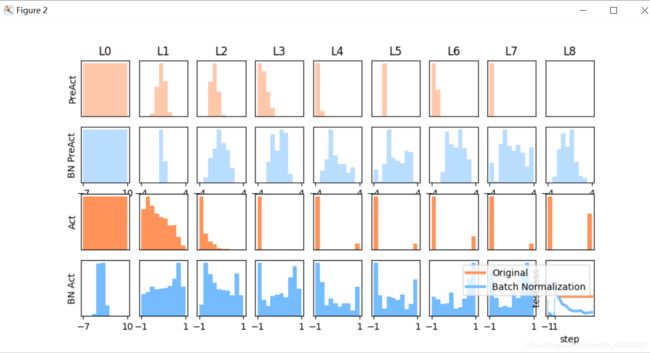
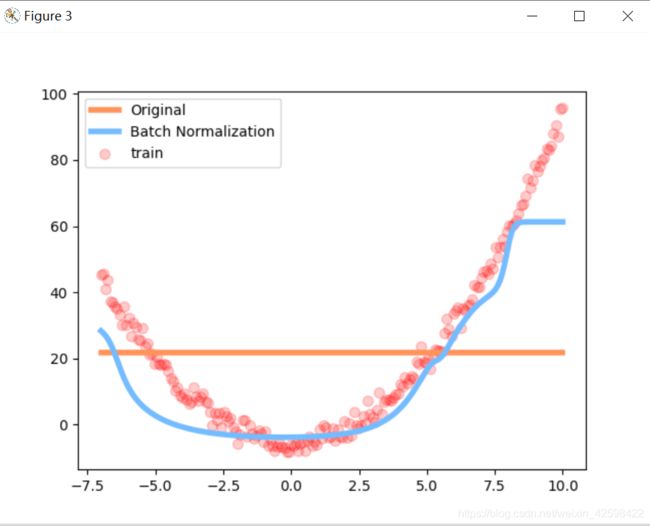
13.batch normalization使得数据被更好的利用

import torch
from torch import nn
from torch.nn import init
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np

# torch.manual_seed(1)    # reproducible
# np.random.seed(1)

# Hyper parameters
N_SAMPLES = 2000
BATCH_SIZE = 64
EPOCH = 12
LR = 0.03
N_HIDDEN = 8
ACTIVATION = torch.tanh
B_INIT = -0.2   # use a bad bias constant initializer

# training data
x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]
noise = np.random.normal(0, 2, x.shape)
y = np.square(x) - 5 + noise

# test data
test_x = np.linspace(-7, 10, 200)[:, np.newaxis]
noise = np.random.normal(0, 2, test_x.shape)
test_y = np.square(test_x) - 5 + noise

train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()
test_x = torch.from_numpy(test_x).float()
test_y = torch.from_numpy(test_y).float()

train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

# show data
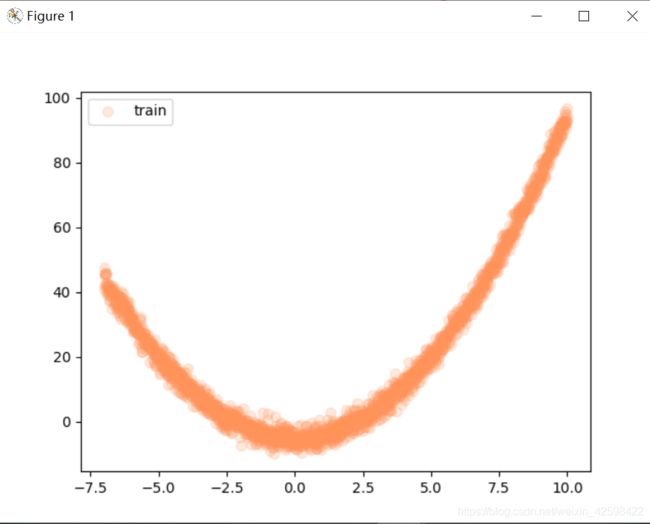
plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')
plt.legend(loc='upper left')


class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        self.do_bn = batch_normalization
        self.fcs = []
        self.bns = []
        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   # for input data

        for i in range(N_HIDDEN):               # build hidden layers and BN layers
            input_size = 1 if i == 0 else 10
            fc = nn.Linear(input_size, 10)
            setattr(self, 'fc%i' % i, fc)       # IMPORTANT set layer to the Module
            self._set_init(fc)                  # parameters initialization
            self.fcs.append(fc)
            if self.do_bn:
                bn = nn.BatchNorm1d(10, momentum=0.5)
                setattr(self, 'bn%i' % i, bn)   # IMPORTANT set layer to the Module
                self.bns.append(bn)

        self.predict = nn.Linear(10, 1)         # output layer
        self._set_init(self.predict)            # parameters initialization

    def _set_init(self, layer):
        init.normal_(layer.weight, mean=0., std=.1)
        init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        pre_activation = [x]
        if self.do_bn: x = self.bn_input(x)     # input batch normalization
        layer_input = [x]
        for i in range(N_HIDDEN):
            x = self.fcs[i](x)
            pre_activation.append(x)
            if self.do_bn: x = self.bns[i](x)   # batch normalization
            x = ACTIVATION(x)
            layer_input.append(x)
        out = self.predict(x)
        return out, layer_input, pre_activation

nets = [Net(batch_normalization=False), Net(batch_normalization=True)]

# print(*nets)    # print net architecture

opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]

loss_func = torch.nn.MSELoss()


def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):
    for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):
        [a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]
        if i == 0:
            p_range = (-7, 10);the_range = (-7, 10)
        else:
            p_range = (-4, 4);the_range = (-1, 1)
        ax_pa.set_title('L' + str(i))
        ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)
        ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')
        for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())
        ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)
        axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')
    plt.pause(0.01)


if __name__ == "__main__":
    f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))
    plt.ion()  # something about plotting
    plt.show()

    # training
    losses = [[], []]  # recode loss for two networks

    for epoch in range(EPOCH):
        print('Epoch: ', epoch)
        layer_inputs, pre_acts = [], []
        for net, l in zip(nets, losses):
            net.eval()              # set eval mode to fix moving_mean and moving_var
            pred, layer_input, pre_act = net(test_x)
            l.append(loss_func(pred, test_y).data.item())
            layer_inputs.append(layer_input)
            pre_acts.append(pre_act)
            net.train()             # free moving_mean and moving_var
        plot_histogram(*layer_inputs, *pre_acts)     # plot histogram

        for step, (b_x, b_y) in enumerate(train_loader):
            for net, opt in zip(nets, opts):     # train for each network
                pred, _, _ = net(b_x)
                loss = loss_func(pred, b_y)
                opt.zero_grad()
                loss.backward()
                opt.step()    # it will also learns the parameters in Batch Normalization

    plt.ioff()

    # plot training loss
    plt.figure(2)
    plt.plot(losses[0], c='#FF9359', lw=3, label='Original')
    plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')
    plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')

    # evaluation
    # set net to eval mode to freeze the parameters in batch normalization layers
    [net.eval() for net in nets]    # set eval mode to fix moving_mean and moving_var
    preds = [net(test_x)[0] for net in nets]
    plt.figure(3)
    plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')
    plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')
    plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')
    plt.legend(loc='best')
    plt.show()