基于R语言的主成分分析
目录
1.主成分分析步骤
2.常用函数
1.princomp函数
2.summary函数
3.loadings函数
4.predict函数
5.screeplot函数
3.代码实现
1.主成分分析步骤
(1)将数据标准化
(2)求样本的相关系数矩阵R
(3)求R的特征值以及特征向量
(4)按主成分累计贡献率超过85%来确定主成分的个数K,并写出主成分表达式
(5)对分析结果做统计意义和实际意义的解释
2.常用函数
1.princomp函数
用于计算相关矩阵R做主成分分析
函数格式:
princomp(x,cor=FALSE,scores=TRUE,...)2.summary函数
用来提取主成分信息
函数格式:
summary(object,loadings=FALSE)3.loadings函数
用于显示主成分信息
函数格式:
loadings(object)4.predict函数
用于预测主成分的值
函数格式:
predict(object,newdata,...)5.screeplot函数
用于绘制出主成分的碎石图
函数格式:
screeplot(object,type=c("barplot","lines",...))3.代码实现
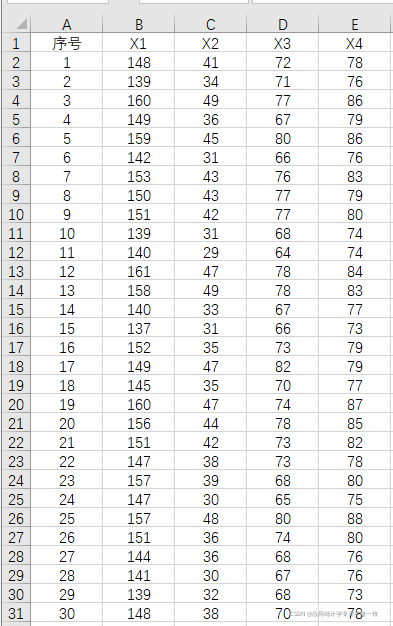
随机抽取30名某年级中 学生,测量其身高(X1), 体重(X2), 胸围(X3), 坐高(X4), 数据如下表所示, 试对 这30名学生身体四项指标作主成分分析
计算过程:
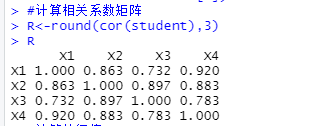
(1)计算相关系数矩阵:
#读取数据
data<-read.table("D:/桌面文件/4.txt",header = T)
#变量赋值数据框
student<-data.frame(X1=data[2],
X2=data[3],
X3=data[4],
X3=data[5])
#计算相关系数矩阵
R<-round(cor(student),3)
R运行结果:
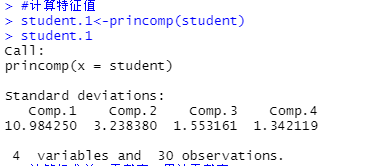
(2)计算样本相关系数矩阵的特征值:
#计算特征值
student.1<-princomp(student)
student.1运行结果:
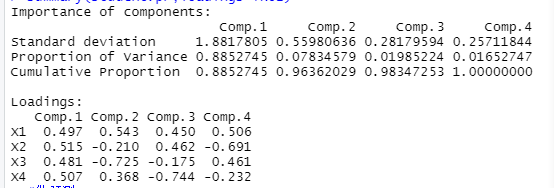
(3)计算标准差,贡献率,累计贡献率:
#计算标准差,贡献率,累计贡献率
student.pr<-princomp(student.pr,cor=TRUE)
summary(student.pr,loadings=TRUE)运行结果:
注:
Standard deviation: 表示主成分的标准差, 即主成分的方差平方根, 即 相应特征值的开方
Proportion of Variance: 表示方差的贡献率;
Cumulative Proportion: 表示方差的累计贡献率
从图中可知,第一个的贡献率就达到了88.52%,前两个累计贡献率达到了96.36%,那么我们可以取两个主成分达到将为处理的目的即可。第一主成分和第二主成分分别为:
Z1=0.497X1+0.515X2+0.481X3+0.507X4
Z2=0.543X1-0.210X2-0.725X3+0.368X4
结果解释:
由Z1的系数都接近与0.5, 它反映学生身材的魁 梧程度,因此我们称第一主成分为身材大小因子; Z2的系数中体 重(X2)和胸围(X3)为正值, 它反映学生的胖瘦情况,故称第二主成分为胖瘦因子。
(4)画出碎石图:
#画出碎石图
screeplot(student.pr,type = "lines")运行结果:
从图中可知,在第二主成分后趋于平稳,符合选取两个主成分的结论。
(5)绘制载荷散点图
#提取主成分载荷矩阵
load<-loadings(student.pr)
#用载荷前两列做散点图
plot(load[,1:2],xlim=c(-0.9,0.9),ylim=c(-0.9,0.9))
#标记序号
text(load[,1],load[,2],adj=c(0.9,-0.9))
#划分象限
abline(h=0);abline(v=0)运行结果:
从图中可以看出,两个主成分载荷散点图与前面叙述的结论特征相符。