深度学习——损失函数推导过程(三个方面诠释损失函数的由来意义)
三个维度诠释损失函数
我们在学习机器学习的过程中,通常利用损失函数来衡量模型所做出的预测离真实值之间的偏离程度。
损失函数大致分为3类方法
- 最小二乘法
- 极大似然估计法
- 交叉熵
1.最小二乘法
这个方法是最显而易懂的,假设x是真实值,y是预测值,那么
∣ x − y ∣ |x-y| ∣x−y∣
式子(1)就是指真实值与预测值之间的偏差。这只是对一次样本,那么对于全部样本(数据集中包含n个样本),就要做累和:
∑ i = 1 n ∣ x i − y i ∣ \sum_{i=1}^n|x_i-y_i| i=1∑n∣xi−yi∣
我们在求解过程中,需要求式子的最小值来对模型进行判断,那么公式二我们可以知道该式子是不连续的,即不可求导 【为什么?文章最后提到:①注解】,于是我们在此基础是加上²,使该式子连续且可导,那么最后损失函数的第一种也就出来了
min ∑ i = 1 n ∣ x i − y i ∣ 2 \min\sum_{i=1}^n|x_i-y_i|^2 mini=1∑n∣xi−yi∣2
2.极大似然估计法
在学习该方法之前,我们需要先了解,什么是似然。在理论和现实之间总存在差异,也就是理论可以推导预判现实,而对于现实是不可以推导出真实的理论,但是能够与理论靠近。这里可以举个例子,我们知道每次丢硬币的正负两面出现的概率都是1:1,我们一次丢两枚硬币,两枚都向上或都向下的概率应该为1/2*1/2=1/4,如果我们不知道这个理论,随机丢5次,可能运气差点,每次两枚硬币都朝上,这样现实中我们仅仅靠观测到的概率就和理论明显存在差异了。所以我们应该做多次实验,尽可能让其数据达到平稳,也就是让其靠近实际理论。这就是似然。
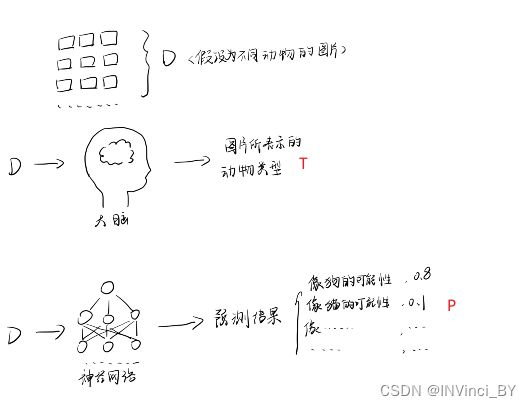
在神经网络中,理论模型就好比我们人类的大脑,而我们需要不断去训练神经网络,使其靠近我们大脑的评估模式。因此也能够这样理解,一组待检测样本数据D,D经过人类大脑,被赋予含义T,再将D输入到神经网络中,得到模拟模型的结果P。
这里我们简化一下,假设所有输入的图片只有一种类型cat,我们只需判断它是不是cat,对于真实值1表示是cat,0表示不是cat,对于训练的预测值表示其像cat的概率。
在训练神经网络模型其实就是训练其参数W,b。在(W,b)模型下,单个样本得到正确检测结果的概率为(假设x是样本真实值,y是神经网络预测值)
P ( x ∣ ( W , b ) ) P(x|(W,b)) P(x∣(W,b))
那么全体样本是真实值的概率就是单个样本的累积
∏ i = 1 n P ( x i ∣ ( W , b ) ) \prod_{i=1}^nP(x_i|(W,b)) i=1∏nP(xi∣(W,b))
而y=f(W,b),可以用y替代(W,b),得到
∏ i = 1 n P ( x i ∣ y i ) \prod_{i=1}^nP(x_i|y_i) i=1∏nP(xi∣yi)
求这个式子的最大值,在求解过程中,我们习惯利用加法来简化求解的复杂性,因此这里将其进行log求指数,使累积变成累和并且不改变其单调性
log ∏ i = 1 n P ( x i ∣ y i ) = ∑ i = 1 n log P ( x i ∣ y i ) \log\prod_{i=1}^nP(x_i|y_i)\\=\sum_{i=1}^n\log P(x_i|y_i)\\ logi=1∏nP(xi∣yi)=i=1∑nlogP(xi∣yi)
对于x,我们知道其属于伯努利分布:
f = { p x = 1 1 − p x = 0 f=\begin{cases}p & x=1 \\1-p & x=0 \\\end{cases} f={p1−px=1x=0
那么其概率分布函数可以写成
f ( x ) = p x ( 1 − p ) 1 − x f(x) = p^x(1-p)^{1-x} f(x)=px(1−p)1−x
对应在公式(7)中
∑ i = 1 n log P ( x i ∣ y i ) = ∑ i = 1 n log y i x i ( 1 − y i ) 1 − x i = ∑ i = 1 n x i log y i + ∑ i = 1 n ( 1 − x i ) log ( 1 − y i ) \sum_{i=1}^n\log P(x_i|y_i)\\=\sum_{i=1}^n\log y_i^{x_i}(1-y_i)^{1-x_i}\\=\sum_{i=1}^nx_i\log y_i+\sum_{i=1}^n(1-x_i)\log (1-y_i) i=1∑nlogP(xi∣yi)=i=1∑nlogyixi(1−yi)1−xi=i=1∑nxilogyi+i=1∑n(1−xi)log(1−yi)
于是第二种损失函数就是
∑ i = 1 n x i log y i + ∑ i = 1 n ( 1 − x i ) log ( 1 − y i ) \sum_{i=1}^nx_i\log y_i+\sum_{i=1}^n(1-x_i)\log (1-y_i) i=1∑nxilogyi+i=1∑n(1−xi)log(1−yi)
3.交叉熵
这里我们需要了解一个概念,就是公式是如何被定义的。
我们知道在力学里面
F : = m a F:=ma F:=ma
但是也有
F = G M m r 2 F=G\frac {Mm}{r^2} F=Gr2Mm
这里F:=ma并不代表力等于ma,而是被定义为ma。其中可以加入其它常量,不改变其性质即可。由此我们可以进入下一步。
信息量表示某个事件所带来的含义,信息量越大,整个事件的不确定性也就越大。换句话说也可以表示该事件发生的概率越小。
以最近很火的世界杯为例,事件F1(中国队世界杯夺冠),和事件F2(阿根廷世界杯夺冠),F1和F2哪个发生所带来的信息量大呢?显然是F1。这里可能有人不理解为什么是F1,就好比我说了两句话
a:世界杯成功举办了
b:枯藤老树昏鸦
a只传达了世界杯成功举报一个信息,而b传达的是三个物体以及他们的三种不同属性。同样,我们知道中国队世界杯夺冠的可能性远远小于阿根廷,因此当F1发生时,我们会获得大量信息,其中包括了对该事件发生的不理解以及震惊(当然阿根廷队夺冠我们也会有情感上的波动,但是这里大家懂的都懂)。
于是我们可以将信息量与概率关联起来:
F1的信息量包含了F3(中国队挺进世界杯决赛)以及F4(中国队决赛胜利)
F1的概率是F3的概率乘以F4的概率
F ( 1 ) = F ( 3 ) + F ( 4 ) P ( 1 ) = P ( 3 ) ∗ P ( 4 ) F(1)=F(3)+F(4)\\P(1) = P(3)*P(4) F(1)=F(3)+F(4)P(1)=P(3)∗P(4)
所以我们在表示信息量的时候可以引入概率这个属性特征,而我们知道信息量是累积,概率是累和,因此这里可以引入log,使其计算发生变换,与此同时,信息量与概率成反比,最后要在式子前面加入一个符号,这样信息量的定义就完成了
F ( x ) : = − log P ( x ) F(x):=-\log P(x) F(x):=−logP(x)
回到深度学习神经网络,如何使模型接近完美的理想模型,这里就提出了相对熵的概念(KL散度):考虑某个未知的分布p,假设用一个近似分布q对它进行建模
D K L ( p ∣ ∣ q ) = ∑ i = 1 n p ( x i ) log p ( x i ) q ( x i ) = ∑ i = 1 n p ( x i ) log p ( x i ) − ∑ i = 1 n p ( x i ) log q ( x i ) = ∑ i = 1 n p ( x i ) ( − log q ( x i ) ) − ∑ i = 1 n p ( x i ) ( − log p ( x i ) ) = 交 叉 熵 − 信 息 熵 D_{KL}(p||q)\\=\sum_{i=1}^np(x_i)\log \frac{p(x_i)}{q(x_i)}\\=\sum_{i=1}^np(x_i)\log p(x_i)-\sum_{i=1}^np(x_i)\log q(x_i)\\=\sum_{i=1}^np(x_i)(-\log q(x_i))-\sum_{i=1}^np(x_i)(-\log p(x_i))\\=交叉熵-信息熵 DKL(p∣∣q)=i=1∑np(xi)logq(xi)p(xi)=i=1∑np(xi)logp(xi)−i=1∑np(xi)logq(xi)=i=1∑np(xi)(−logq(xi))−i=1∑np(xi)(−logp(xi))=交叉熵−信息熵
根据证明DKL恒大于等于0,因此其值越小,说明模型相近度越高。
交叉熵越大,其模型消除不确定性的努力越大。
应用到神经网络,这里P相当于人类大脑的模型,相当于我们实现对样本数据进行的标注,也就是说P是确定的,于是p的信息熵也就是确定的,我们要求DKL的最小值,也就是求交叉熵的最小值。
q表示预测的结果,我们从数据上看,p=1表示这个是cat,p=0表示这个表示cat,p表示了是和不是两种情况的可能性,而q仅仅表示的是该物体近似cat的可能性,于是我们需要对q进行变化,其不能直接用预测值y进行表示
交 叉 熵 = ∑ i = 1 n p ( x i ) ( − log q ( x i ) ) = ∑ i = 1 n x i log y i + ( 1 − x i ) l o g ( 1 − y i ) ) 交叉熵=\sum_{i=1}^np(x_i)(-\log q(x_i))\\=\sum_{i=1}^nx_i\log y_i+(1-x_i)log(1-y_i)) 交叉熵=i=1∑np(xi)(−logq(xi))=i=1∑nxilogyi+(1−xi)log(1−yi))
虽然这个式子与最大估计似然方法得到的式子一样,但是从推导上看,我们可以知道前者的log是从定义上来的,而后者的log是从方便计算上来的。
注解
①为什么|x-y|不可导?
我们将公式变换一下,我们希望|x-y|=0,在这种情况下,是最理想的模型(当然对于大部分应用模型,这种情况是很少的),那么在理想情况下该公式可变为y=|x|,这个式子在全体定义域上其实就是分段函数:
y = { x x ≥ 0 − x x < 0 y=\begin{cases}x & x\geq0 \\-x & x<0 \\\end{cases} y={x−xx≥0x<0
是不连续的,当对其加平方之后,相当于|x|²,即使其可连续可导。
若有问题,欢迎指出