PyTorch深度学习实践

目录

LESSON 1 线性模型

LESSON 2 梯度下降

LESSON 3 随机梯度下降

LESSON 4 反向传播

LESSON 5 Pytorch实现线性回归

LESSON 6 逻辑斯蒂回归

LESSON 7 处理多维特征的输入

 LSEEON 8 加载数据集--实验mini-batch

LESSON 9 多分类问题

 LESSON 10 卷积神经网络一

 LESSON 11 卷积神经网络二

 LESSON 12 循环神经网络一

LESSON 13 循环神经网络二

---

LESSON 1 线性模型

代码说明：1、函数forward()中，有一个变量w。这个变量最终的值是从for循环中传入的。

                  2、for循环中，使用了np.arange。

                 3、python中zip()函数的用法
 

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

def forward(x):
    return x*w

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y) **2

w_list=[]
mse_list=[]

for w in np.arange(0.0,4.1,0.1):
    w_list.append(w)
    l_sum = 0
    for x,y in zip(x_data,y_data):
        y_pre = forward(x)
        loss_val=loss(x,y)
        l_sum += loss_val
    mse_list.append(l_sum/3)


plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

 作业：

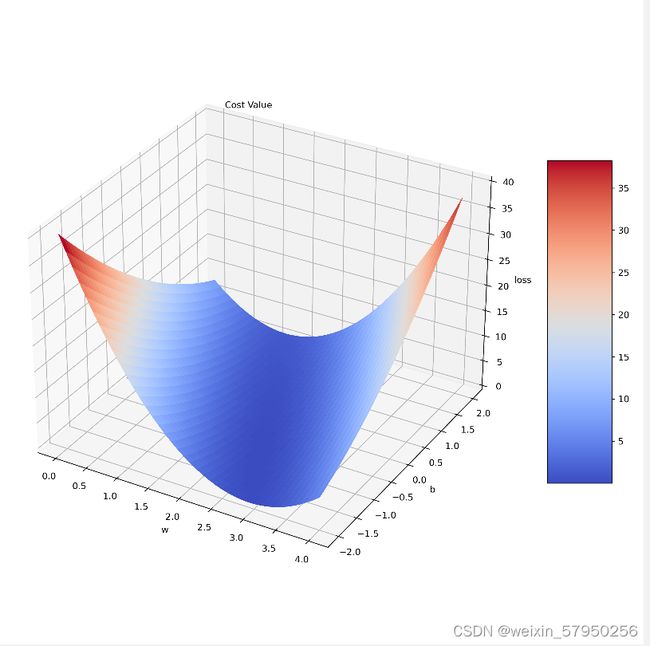
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

# y = x*2.5-1 构造训练数据
x_data = [1.0, 2.0, 3.0]
y_data = [1.5, 4.0, 6.5]
W, B = np.arange(0.0, 4.1, 0.1), np.arange(-2.0, 2.1, 0.1)  # 规定 W,B 的区间
w, b = np.meshgrid(W, B, indexing='ij')  # 构建矩阵坐标


def forward(x):
    return x * w + b


def loss(y_pred, y):
    return (y_pred - y) * (y_pred - y)


# Make data.
mse_lst = []
l_sum = 0.
for x_val, y_val in zip(x_data, y_data):
    y_pred_val = forward(x_val)
    loss_val = loss(y_pred_val, y_val)
    l_sum += loss_val
mse_lst.append(l_sum / 3)

# 定义figure
fig = plt.figure(figsize=(10, 10), dpi=300)
# 将figure变为3d
ax = Axes3D(fig,auto_add_to_figure=False)
fig.add_axes(ax)
# 绘图，rstride:行之间的跨度  cstride:列之间的跨度
surf = ax.plot_surface(w, b, np.array(mse_lst[0]), rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0,
                       antialiased=False)
# Customize the z axis.
ax.set_zlim(0, 40)
# 设置坐标轴标签
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("loss")
ax.text(0.2, 2, 43, "Cost Value", color='black')
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()

LESSON 2 梯度下降

梯度下降

import matplotlib.pyplot as plt


x_data = [1.0, 2.0, 3.0]
y_data = [1.5, 4.0, 6.5]

w = 1.0

epoch_list = []
cost_list = []

def forward(x):
    return x * w


def cost(x_data, y_data):
    cost_ans = 0
    for x,y in zip(x_data,y_data):
        y_pre = forward(x)
        cost_ans += (y_pre - y) ** 2
    return cost_ans / len(x_data)


def gradient(x_data, y_data):
    grad = 0
    for x,y in zip(x_data,y_data):
        grad += 2 * x * (x * w - y)
    return grad / len(x_data)

for epoch in range(100):
    loss = cost(x_data, y_data)
    w -= 0.01 * gradient(x_data,y_data)
    print('epoch:', epoch, 'w=', w, 'loss=', loss)
    epoch_list.append(epoch)
    cost_list.append(loss)

print('predict (after training)', 4, forward(4))
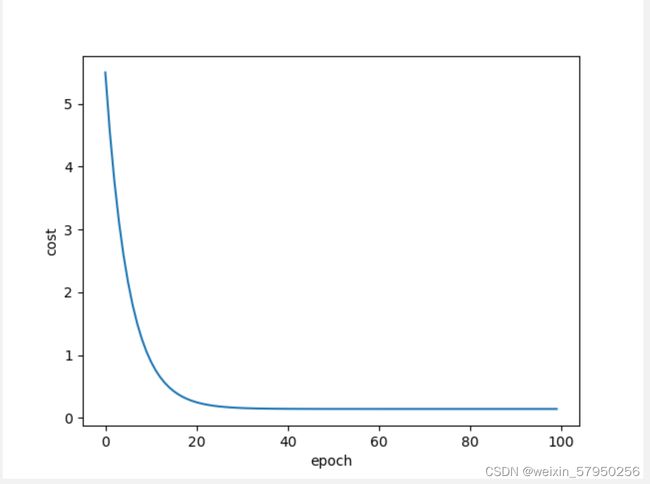
plt.plot(epoch_list,cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()

结果

 

LESSON 3 随机梯度下降

随机梯度下降法

随机梯度下降法在神经网络中被证明是有效的。效率较低(时间复杂度较高)，学习性能较好。

随机梯度下降法和梯度下降法的主要区别在于：

1、损失函数由cost()更改为loss()。cost是计算所有训练数据的损失，loss是计算一个训练数据的损失。对应于源代码则是少了两个for循环。

2、梯度函数gradient()由计算所有训练数据的梯度更改为计算一个训练数据的梯度。

3、本算法中的随机梯度主要是指，每次拿一个训练数据来训练，然后更新梯度参数。本算法中梯度总共更新100(epoch)x3 = 300次。梯度下降法中梯度总共更新100(epoch)次。

import matplotlib.pyplot as plt


x_data = [1.0, 2.0, 3.0]
y_data = [1.5, 4.0, 6.5]

w = 1.0

epoch_list = []
loss_list = []

def forward(x):
    return x * w


def loss(x, y):
    y_pre = forward(x)
    return (y_pre - y) ** 2


def gradient(x, y):
    return 2 * x *(x * w - y)

for epoch in range(100):
    for x,y in zip(x_data, y_data):
        l = loss(x, y)
        w -= 0.01 * gradient(x, y)
    print("progress:", epoch, "w=", w, "loss=", l)
    epoch_list.append(epoch)
    loss_list.append(l)

print('predict (after training)', 4, forward(4))
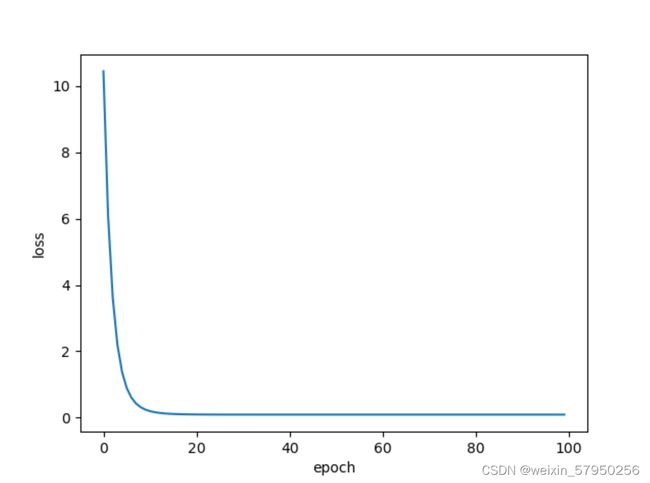
plt.plot(epoch_list,loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

实验结果

LESSON 4 反向传播

1、w是Tensor(张量类型)，Tensor中包含data和grad，data和grad也是Tensor。grad初始为None，调用l.backward()方法后w.grad为Tensor，故更新w.data时需使用w.grad.data。如果w需要计算梯度，那构建的计算图中，跟w相关的tensor都默认需要计算梯度。

刘老师视频中a = torch.Tensor([1.0]) 本文中更改为 a = torch.tensor([1.0])。两种方法都可以
 

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [1.5, 4.0, 6.5]

w = torch.Tensor([1.0])
w.requires_grad = True

def forward(x):
    return x * w

def loss(x,y):
    y_pre = forward(x)
    return (y_pre - y)** 2


for epoch in range(100):
    for x,y in zip(x_data,y_data):
        l = loss(x,y)
        l.backward()
        w.data = w.data - 0.01 * w.grad.data
        w.grad.data.zero_()
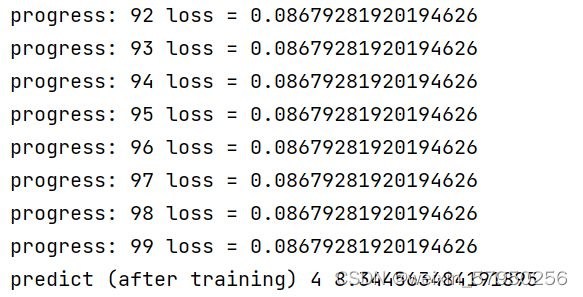
    print('progress:', epoch, 'loss =',l.item())

print("predict (after training)", 4, forward(4).item())

实验结果

 作业

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w1 = torch.Tensor([1.0])
w1.requires_grad = True

w2 = torch.Tensor([1.0])
w2.requires_grad = True

b = torch.Tensor([1.0])
b.requires_grad = True

def forward(x):
    return x * x * w1 + x * w2 + b

def loss(x,y):
    y_pre = forward(x)
    return (y_pre - y)** 2


for epoch in range(100):
    for x,y in zip(x_data,y_data):
        l = loss(x,y)
        l.backward()
        w1.data = w1.data - 0.01 * w1.grad.data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print('progress:', epoch, 'loss =',l.item())

print("predict (after training)", 4, forward(4).item())

实验结果

LESSON 5 Pytorch实现线性回归

PyTorch Fashion(风格)

1、prepare dataset

2、design model using Class  # 目的是为了前向传播forward，即计算y hat(预测值)

3、Construct loss and optimizer (using PyTorch API) 其中，计算loss是为了进行反向传播，optimizer是为了更新梯度。

4、Training cycle (forward,backward,update)
 

import torch

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])

class LinearModule(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = torch.nn.Linear(1,1)
    def forward(self,x):
        y_pre = self.linear(x)
        return y_pre

model = LinearModule()
l = torch.nn.MSELoss(reduction = 'sum')
optimizer = torch.optim.SGD(model.parameters(),0.01)

for epoch in range(100):
    y_pre = model(x_data)
    loss = l(y_pre,y_data)
    print(epoch, loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

x_test = torch.tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

实验结果

LESSON 6 逻辑斯蒂回归

说明：1、 逻辑斯蒂回归和线性模型的明显区别是在线性模型的后面，添加了sigmoid函数

          2、分布的差异：KL散度，cross-entropy交叉熵

import torch
# import torch.nn.functional as F
 
# prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0.0], [0.0], [1.0]])
 
#design model using class
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1,1)
 
    def forward(self, x):
        # y_pred = F.sigmoid(self.linear(x))
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred
model = LogisticRegressionModel()
 
# construct loss and optimizer
# 默认情况下，loss会基于element平均，如果size_average=False的话，loss会被累加。
criterion = torch.nn.BCELoss(size_average = False) 
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
 
# training cycle forward, backward, update
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
 
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
 
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
 
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data.item())

LESSON 7 处理多维特征的输入

import torch
import numpy as np
import matplotlib.pyplot as plt

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)
x = torch.from_numpy(xy[:, :-1])
y = torch.from_numpy(xy[:, [-1]])

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8,6)
        self.linear2 = torch.nn.Linear(6,4)
        self.linear3 = torch.nn.Linear(4,1)
        self.activate = torch.nn.Sigmoid()
    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))
        x = self.activate(self.linear3(x))
        return x

model = Model()
criterion = torch.nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)

epoch_list = []
loss_list = []

for epoch in  range(100):
    y_pre = model(x)
    loss = criterion(y_pre, y)
    print(epoch, loss.item())
    epoch_list.append(epoch)
    loss_list.append(loss.item())

    optimizer.zero_grad()
    loss.backward()

    optimizer.step()

plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
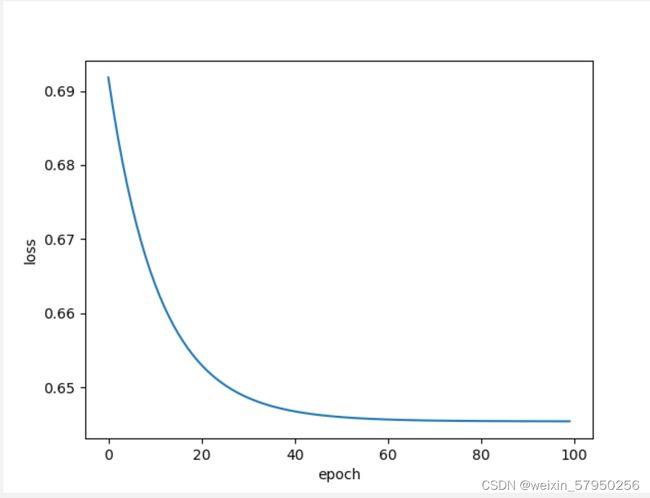
plt.show()

实验结果

 

 LSEEON 8 加载数据集--实验mini-batch

假如有10,000个样本，batch大小为1,000，此时iteration=10 

说明：1、DataSet 是抽象类，不能实例化对象，主要是用于构造我们的数据集

          2、DataLoader 需要获取DataSet提供的索引[i]和len;用来帮助我们加载数据，比如说做shuffle(提高数据集的随机性)，batch_size,能拿出Mini-Batch进行训练。它帮我们自动完成这些工作。DataLoader可实例化对象。DataLoader is a class to help us loading data in Pytorch.

         3、__getitem__目的是为支持下标(索引)操作
 

import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader


class DiabetesDataSet(Dataset):
    def __init__(self,filename):
        xy = np.loadtxt(filename,delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]  # shape(多少行，多少列)
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
    def __getitem__(self, item):
        return self.x_data[item], self.y_data[item]
    def __len__(self):
        return self.len

dataset = DiabetesDataSet('diabetes.csv.gz')
train_loader = DataLoader(dataset= dataset, batch_size= 32, shuffle= True,num_workers=0)

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8,6)
        self.linear2 = torch.nn.Linear(6,4)
        self.linear3 = torch.nn.Linear(4,1)
        self.activate = torch.nn.Sigmoid()
    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))
        x = self.activate(self.linear3(x))
        return x

model = Model()
criterion = torch.nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)


for epoch in range(100):
    for i, data in enumerate(train_loader,0):
        inputs, labels = data
        labels_pre = model(inputs)
        loss = criterion(labels_pre,labels)

        optimizer.zero_grad()
        loss.backward()

        optimizer.step()

        print(epoch, i, loss.item())

实验结果：

LESSON 9 多分类问题

说明：

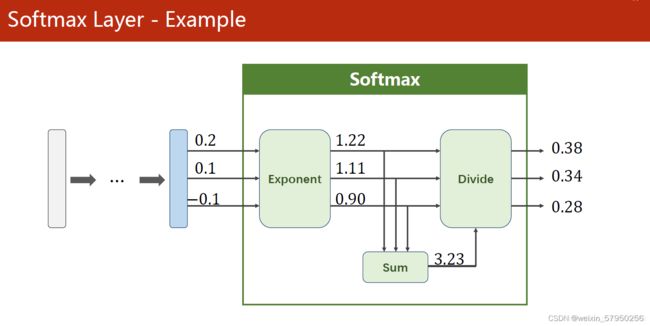
1、softmax的输入不需要再做非线性变换，也就是说softmax之前不再需要激活函数(relu)。softmax两个作用，如果在进行softmax前的input有负数，通过指数变换，得到正数。所有类的概率求和为1。

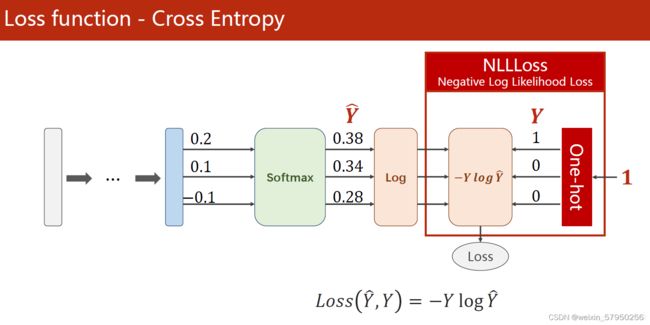
2、y的标签编码方式是one-hot。我对one-hot的理解是只有一位是1，其他位为0。(但是标签的one-hot编码是算法完成的，算法的输入仍为原始标签)

3、多分类问题，标签y的类型是LongTensor。比如说0-9分类问题，如果y = torch.LongTensor([3])，对应的one-hot是[0,0,0,1,0,0,0,0,0,0].(这里要注意，如果使用了one-hot，标签y的类型是LongTensor，糖尿病数据集中的target的类型是FloatTensor)

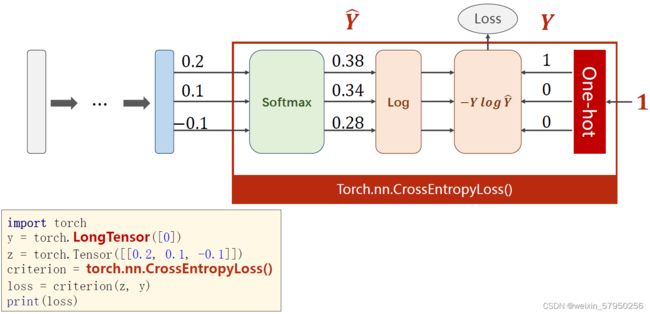
4、CrossEntropyLoss <==> LogSoftmax + NLLLoss。也就是说使用CrossEntropyLoss最后一层(线性层)是不需要做其他变化的；使用NLLLoss之前，需要对最后一层(线性层)先进行SoftMax处理，再进行log操作。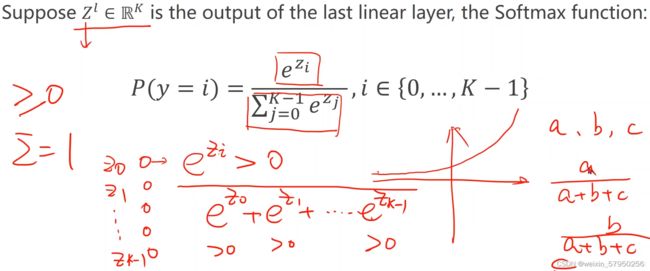

代码说明：

1、第8讲 from torch.utils.data import Dataset，第9讲 from torchvision import datasets。该datasets里面init，getitem,len魔法函数已实现。

2、torch.max的返回值有两个，第一个是每一行的最大值是多少，第二个是每一行最大值的下标(索引)是多少。
 

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
 
# prepare dataset
 
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
 
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
 
# design model using class
 
 
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)
 
    def forward(self, x):
        x = x.view(-1, 784)  # -1其实就是自动获取mini_batch
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)  # 最后一层不做激活，不进行非线性变换
 
 
model = Net()
 
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
 
# training cycle forward, backward, update
 
 
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        # 获得一个批次的数据和标签
        inputs, target = data
        optimizer.zero_grad()
        # 获得模型预测结果(64, 10)
        outputs = model(inputs)
        # 交叉熵代价函数outputs(64,10),target（64）
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()
 
        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
            running_loss = 0.0
 
 
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1) # dim = 1 列是第0个维度，行是第1个维度
            total += labels.size(0)
            correct += (predicted == labels).sum().item() # 张量之间的比较运算
    print('accuracy on test set: %d %% ' % (100*correct/total))
 
 
if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

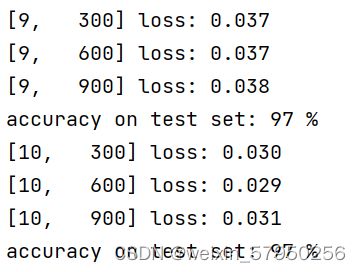
实验结果：

 LESSON 10 卷积神经网络一

说明

0、前一部分叫做Feature Extraction，后一部分叫做classification

1、每一个卷积核它的通道数量要求和输入通道是一样的。这种卷积核的总数有多少个和你输出通道的数量是一样的。

2、卷积(convolution)后，C(Channels)变，W(width)和H(Height)可变可不变，取决于是否padding。subsampling(或pooling)后，C不变，W和H变。

3、卷积层：保留图像的空间信息。

4、卷积层要求输入输出是四维张量(B,C,W,H)，全连接层的输入与输出都是二维张量(B,Input_feature)

卷积操作：

1、若图像为正方形：设输入图像尺寸为WxW，卷积核尺寸为FxF，步幅为S，Padding使用P,经过该卷积层后输出的图像尺寸为NxN：

2、若图像为矩形：设输入图像尺寸为WxH，卷积核的尺寸为FxF，步幅为S，图像深度(通道数)为C，Padding使用P，则：卷积后输出图像大小：， 输出图像的通道数=C

 网络模块：

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)
        self.fc = torch.nn.Linear(320,10)

    def forward(self, x):
        batch_size = x.size(0)
        x = self.pooling(F.relu(self.conv1(x)))
        x = self.pooling(F.relu(self.conv2(x)))
        x = x.view(batch_size,-1)
        x = self.fc(x)
        return x

实验结果：

 LESSON 11 卷积神经网络二

Inception Moudel说明：

1、卷积核超参数选择困难，自动找到卷积的最佳组合。

2、1x1卷积核，不同通道的信息融合。使用1x1卷积核虽然参数量增加了，但是能够显著的降低计算量(operations)

3、Inception Moudel由4个分支组成，要分清哪些是在Init里定义，哪些是在forward里调用。4个分支在dim=1(channels)上进行concatenate。24+16+24+24 = 88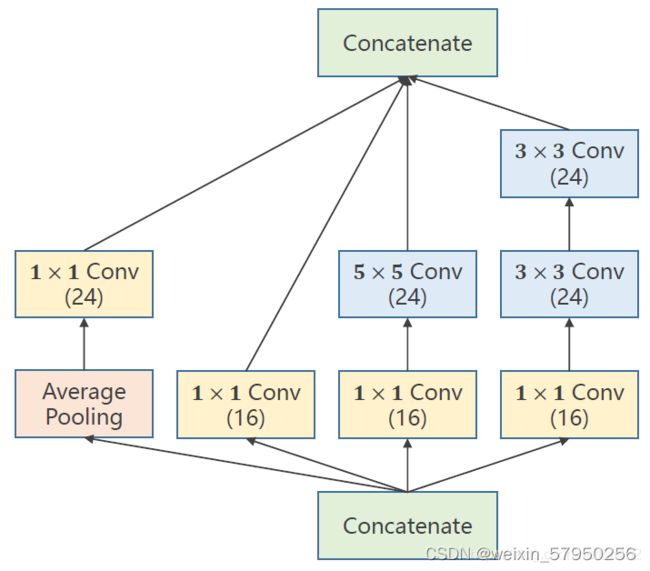

 网络模型

class InceptionA(nn.Module):
    def __init__(self, in_channels):
        super(InceptionA, self).__init__()
        self.branch1x1 = nn.Conv2d(in_channels, 16, kernel_size=1)
 
        self.branch5x5_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch5x5_2 = nn.Conv2d(16, 24, kernel_size=5, padding=2)
 
        self.branch3x3_1 = nn.Conv2d(in_channels, 16, kernel_size=1)
        self.branch3x3_2 = nn.Conv2d(16, 24, kernel_size=3, padding=1)
        self.branch3x3_3 = nn.Conv2d(24, 24, kernel_size=3, padding=1)
 
        self.branch_pool = nn.Conv2d(in_channels, 24, kernel_size=1)
 
    def forward(self, x):
        branch1x1 = self.branch1x1(x)
 
        branch5x5 = self.branch5x5_1(x)
        branch5x5 = self.branch5x5_2(branch5x5)
 
        branch3x3 = self.branch3x3_1(x)
        branch3x3 = self.branch3x3_2(branch3x3)
        branch3x3 = self.branch3x3_3(branch3x3)
 
        branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)
        branch_pool = self.branch_pool(branch_pool)
 
        outputs = [branch1x1, branch5x5, branch3x3, branch_pool]
        return torch.cat(outputs, dim=1) # b,c,w,h  c对应的是dim=1
 
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(88, 20, kernel_size=5) # 88 = 24x3 + 16
 
        self.incep1 = InceptionA(in_channels=10) # 与conv1 中的10对应
        self.incep2 = InceptionA(in_channels=20) # 与conv2 中的20对应
 
        self.mp = nn.MaxPool2d(2)
        self.fc = nn.Linear(1408, 10) 
 
 
    def forward(self, x):
        in_size = x.size(0)
        x = F.relu(self.mp(self.conv1(x)))
        x = self.incep1(x)
        x = F.relu(self.mp(self.conv2(x)))
        x = self.incep2(x)
        x = x.view(in_size, -1)
        x = self.fc(x)
 
        return x

实验结果：

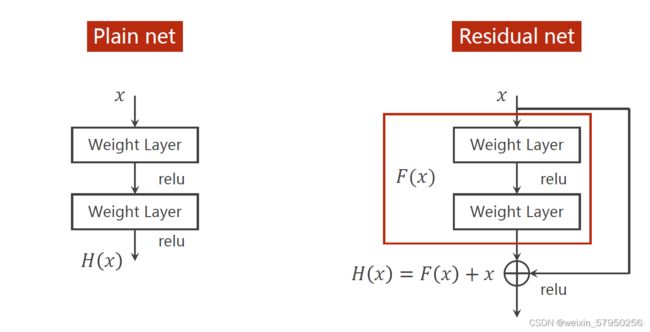
residual network说明：

1、要解决的问题：梯度消失

2、跳连接，H(x) = F(x) + x,张量维度必须一样，加完后再激活。不要做pooling，张量的维度会发生变化。

# design model using class
class ResidualBlock(nn.Module):
    def __init__(self, channels):
        super(ResidualBlock, self).__init__()
        self.channels = channels
        self.conv1 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
 
    def forward(self, x):
        y = F.relu(self.conv1(x))
        y = self.conv2(y)
        return F.relu(x + y)
 
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 16, kernel_size=5)
        self.conv2 = nn.Conv2d(16, 32, kernel_size=5) # 88 = 24x3 + 16
 
        self.rblock1 = ResidualBlock(16)
        self.rblock2 = ResidualBlock(32)
 
        self.mp = nn.MaxPool2d(2)
        self.fc = nn.Linear(512, 10) # 暂时不知道1408咋能自动出来的
 
 
    def forward(self, x):
        in_size = x.size(0)
 
        x = self.mp(F.relu(self.conv1(x)))
        x = self.rblock1(x)
        x = self.mp(F.relu(self.conv2(x)))
        x = self.rblock2(x)
 
        x = x.view(in_size, -1)
        x = self.fc(x)
        return x

实验结果

 LESSON 12 循环神经网络一

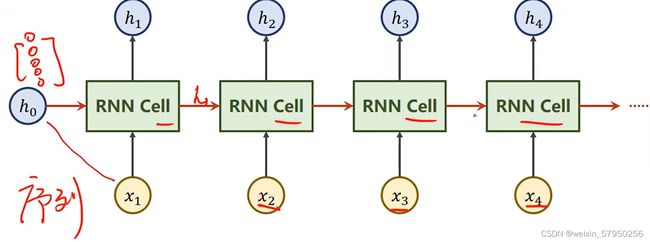
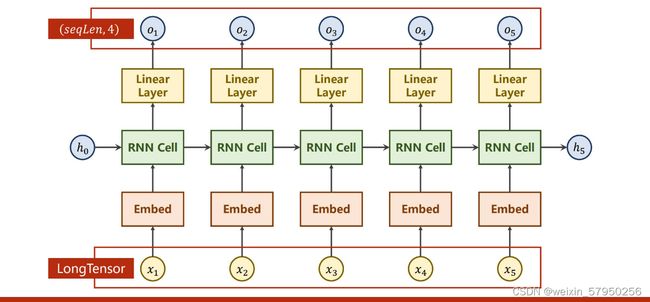
RNN用来处理专门带有序列关系的输入数据

具体结果如下

其中RNN Cell为同一个线性层，伪代码表示

line = LinearModel()
h_0 = 一个向量
for x_i in x:
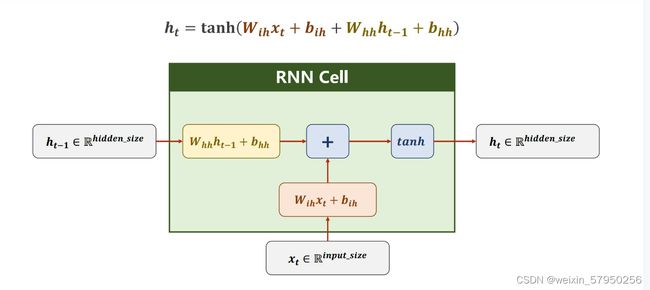
    h_i = line(h_i-1,x_i) #假设i从0开始标号

 

以上图举例说明：

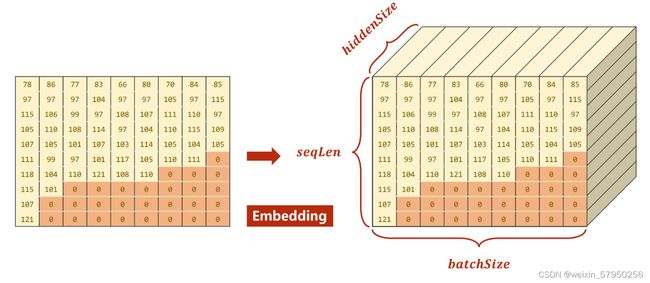
假设输入为X，由于batchSize = 1,说明只有一个样本X，seqLen = 3，说明在X = { x1 ， x2， x3....... }，每3个为一次预测，inputSize = 4，说明 x1，x2，x3都是一个四维向量，hiddenSize = 2，说明h是一个2维向量。

更为形象区分batchSize与seqLen如下：

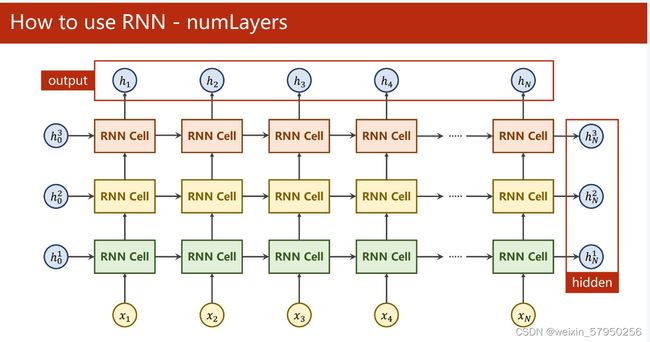
numLayers表示RNN cell的层数，上图的numLayers = 3

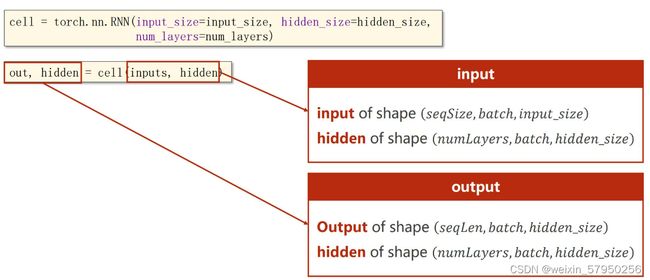
输出形式：output，hidden = cell（inputs，hidden） 

 

使用RNN Cell 

import torch
import torch.optim as optim

idx2Char = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]  # seqLine = 5
one_hot_lookup = [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[i] for i in x_data]
input_size = 4
hidden_size = 4
batch_size = 1
inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)  # view(seqLine,batch_size,input_size)
labels = torch.LongTensor(y_data).view(-1, 1)  # view(seqLine,batch_size)


class Net(torch.nn.Module):
    def __init__(self, input_size, hidden_size, batch_size):
        super(Net, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.batch_size = batch_size
        self.rnnCell = torch.nn.RNNCell(input_size=self.input_size, hidden_size=hidden_size)

    def forward(self, input, hidden):
        hidden = self.rnnCell(input, hidden)
        return hidden

    def init_hidden(self):
        return torch.zeros(self.batch_size, self.hidden_size)


model = Net(input_size, hidden_size, batch_size)

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

for epoch in range(15):
    loss = 0
    optimizer.zero_grad()
    hidden = model.init_hidden()
    print('Predicted string: ', end='')
    # inputs = seqLine*batch_size*input_size, input = batch_size*input_size按序列号取
    # labels = seqLine*1，label = 1
    for input, label in zip(inputs, labels):
        hidden = model(input, hidden)
        loss += criterion(hidden, label)
        _, idx = hidden.max(dim=1)  # 找出hidden认为概率最大的下标
        print(idx2Char[idx.item()], end='')
    loss.backward()
    optimizer.step()
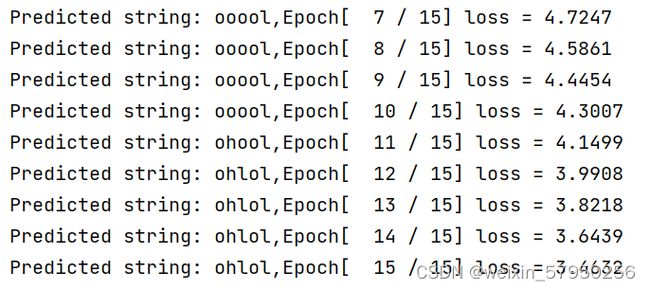
    print(',Epoch[ % d / 15] loss = %.4f' % (epoch + 1, loss.item()))

 实验结果：

使用RNN

import torch
import torch.optim as optim

idx2Char = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]
one_hot_lookup = [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[i] for i in x_data]
input_size = 4
hidden_size = 4
batch_size = 1
num_layers = 1
seqLine = 5
inputs = torch.Tensor(x_one_hot).view(seqLine, batch_size, input_size)  # view(seqLine,batch_size,input_size)
labels = torch.LongTensor(y_data)  # view(seqLine*batch_size，1)


class Net(torch.nn.Module):
    def __init__(self, input_size, hidden_size, batch_size, num_layers=1):
        super(Net, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.batch_size = batch_size
        self.num_layers = num_layers
        self.rnn = torch.nn.RNN(input_size=self.input_size, hidden_size=self.hidden_size, num_layers=self.num_layers)

    def forward(self, input):
        hidden = torch.zeros(self.num_layers, self.batch_size, self.hidden_size)
        out, _ = self.rnn(input, hidden)
        return out.view(-1, self.hidden_size)  # view(seqLen*batch_size,hidden_size)


model = Net(input_size, hidden_size, batch_size, num_layers)

criterion = torch.nn.CrossEntropyLoss() # 要求第一个为二维的Tensor，第二个为一维的labels
optimizer = optim.SGD(model.parameters(), lr=0.5)

for epoch in range(15):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

    _, idx = outputs.max(dim=1)  # dim = 1 表示按行取最大，返回最大的值以及对应下标
    idx = idx.data.numpy()
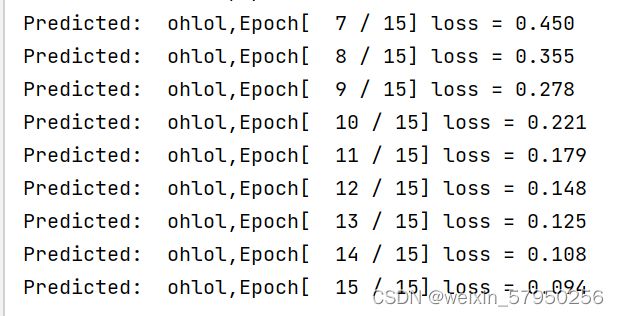
    print('Predicted: ', ''.join([idx2Char[x] for x in idx]), end='')
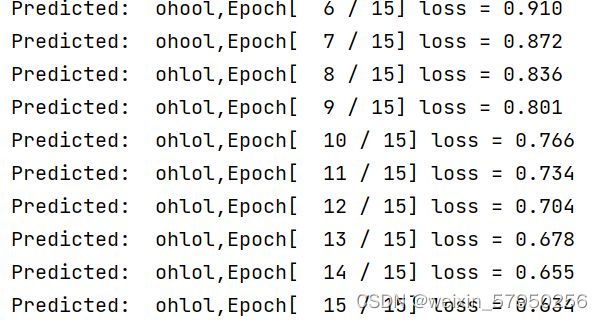
    print(',Epoch[ % d / 15] loss = %.3f' % (epoch + 1, loss.item()))

实验结果

 

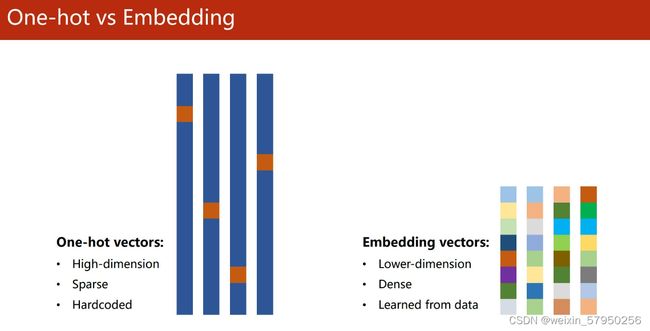
解决办法：使用embedding，就是常说的数据降维

class Net(torch.nn.Module):
    def __init__(self, input_size, hidden_size, batch_size, num_layers, embedding_size, num_class):
        super(Net, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.batch_size = batch_size
        self.num_layers = num_layers
        self.embedding_size = embedding_size
        self.num_class = num_class
        self.em = torch.nn.Embedding(self.input_size, self.embedding_size)
        self.rnn = torch.nn.RNN(input_size=self.embedding_size, hidden_size=self.hidden_size,
                                num_layers=self.num_layers, batch_first=True)  # (batch_size ,seqLen,embedding_size)
        self.fc = torch.nn.Linear(self.hidden_size, self.num_class)  # (batch_size,seqLen,hidden_size)

    def forward(self, x):
        hidden = torch.zeros(self.num_layers, x.size(0), self.hidden_size)
        x = self.em(x)  # (batch_size ,seqLen,embedding_size)
        x, _ = self.rnn(x, hidden)  # (batch_size ,seqLen,hidden_size)
        x = self.fc(x)  # (batch_size,seqLen,num_class)
        return x.view(-1, self.num_class)  # view(batch_size*seqLen,num_class)

实验结果

LESSON 13 循环神经网络二

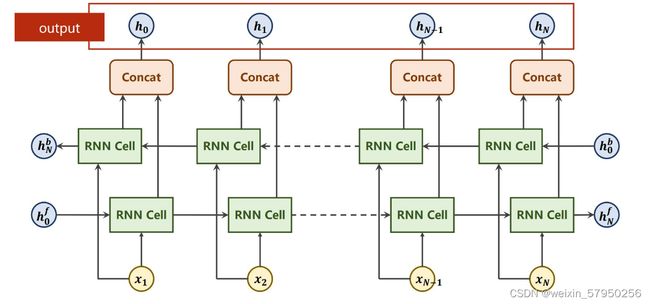
双向循环网络及输出结果 

 为了简便计算，填充的0可以省去，使用packSequence，注意使用这个前提是将向量中的元素降序排序，这里是对每一列进行降序排

import csv
import gzip
import math
import time

import numpy as np
import torch
import torch.optim as optim
from matplotlib import pyplot as plt
from torch import nn
from torch.nn.utils.rnn import pack_padded_sequence
from torch.utils.data import Dataset, DataLoader


class NameDataset(Dataset):
    def __init__(self, is_train_set=True):
        filename = 'names_train.csv.gz' if is_train_set else 'names_test.csv.gz'
        with gzip.open(filename, 'rt') as f:
            reader = csv.reader(f)
            rows = list(reader)
        self.names = [x[0] for x in rows]
        self.countries = [x[1] for x in rows]
        self.len = len(self.names)
        self.country_list = list(sorted(set(self.countries)))
        self.country_dict = self.getCountryDict()
        self.country_num = len(self.country_list)

    def __getitem__(self, item):
        return self.names[item], self.country_dict[self.countries[item]]

    def __len__(self):
        return self.len

    def getCountryDict(self):
        country_dict = dict()
        for idx, country_name in enumerate(self.country_list, 0):
            country_dict[country_name] = idx
        return country_dict

    def idx2Country(self, index):
        return self.country_list[index]

    def getCountryNum(self):
        return self.country_num


# Parameters
HIDDEN_SIZE = 100
BATCH_SIZE = 256
N_LAYER = 2
N_EPOCHS = 100
N_CHARS = 128
USE_GPU = False

trainset = NameDataset(is_train_set=True)
trainLoader = DataLoader(dataset=trainset, batch_size=BATCH_SIZE, shuffle=True)
testset = NameDataset(is_train_set=False)
testLoader = DataLoader(dataset=testset, batch_size=BATCH_SIZE, shuffle=False)
N_COUNTRY = trainset.getCountryNum()


def time_since(since):
    s = time.time() - since
    m = math.floor(s / 60)
    s -= m * 60
    return '%dm %ds' % (m, s)


def create_tensor(tensor):
    if USE_GPU:
        device = torch.device("cuda:0")
        tensor = tensor.to(device)
    return tensor


def name2list(name):
    arr = [ord(c) for c in name]
    return arr, len(arr)


def make_tensor(names, countries):
    sequences_and_lengths = [name2list(x) for x in names]
    name_sequences = [x[0] for x in sequences_and_lengths]
    seq_lengths = torch.LongTensor([x[1] for x in sequences_and_lengths])
    countries = countries.long()

    seq_tensor = torch.zeros(len(name_sequences), seq_lengths.max()).long()
    for idx, (seq, seq_len) in enumerate(zip(name_sequences, seq_lengths), 0):
        seq_tensor[idx, :seq_len] = torch.LongTensor(seq)

    seq_lengths, per_index = seq_lengths.sort(dim=0, descending=True)
    seq_tensor = seq_tensor[per_index]
    countries = countries[per_index]
    return create_tensor(seq_tensor), create_tensor(seq_lengths), create_tensor(countries)


class RNN_GRUClassifier(torch.nn.Module):
    def __init__(self, input_size, hidden_size, output_size, n_layers=1, bidirectional=True):
        super(RNN_GRUClassifier, self).__init__()
        self.hidden_size = hidden_size
        self.n_layers = n_layers
        self.n_directions = 2 if bidirectional else 1

        self.embedding = nn.Embedding(input_size, hidden_size)
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers, bidirectional=bidirectional)
        self.fc = nn.Linear(hidden_size * self.n_directions, output_size)

    def forward(self, input, seq_lengths):
        input = input.t()
        batch_size = input.size(1)
        hidden = self._init_hidden(batch_size)
        embedded = self.embedding(input)
        gru_input = pack_padded_sequence(embedded, seq_lengths)
        output, hidden = self.gru(gru_input, hidden)
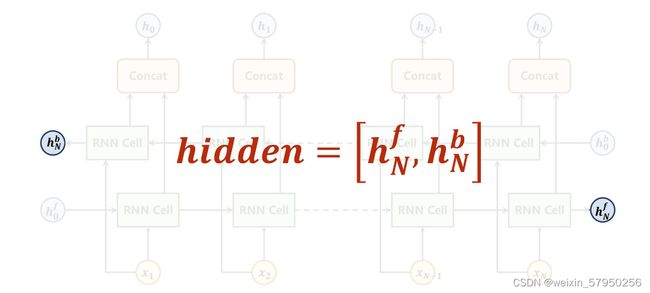
        if self.n_directions == 2:
            hidden_cat = torch.cat([hidden[-1], hidden[-2]], dim=1)
        else:
            hidden_cat = hidden[-1]
        fc_out = self.fc(hidden_cat)
        return fc_out

    def _init_hidden(self, batch_size):
        hidden = torch.zeros(self.n_layers * self.n_directions, batch_size, self.hidden_size)
        return create_tensor(hidden)


def train():
    total_loss = 0
    for i, (names, countries) in enumerate(trainLoader, 1):
        inputs, seq_lengths, target = make_tensor(names, countries)
        outputs = classifier(inputs, seq_lengths)
        loss = criterion(outputs, target)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
        if i % 10 == 0:
            print(f'[{time_since(start)}]Epoch{epoch}', end='')
            print(f'[{i * len(inputs)} / {len(trainset)}]', end='')
            print(f'loss = {total_loss / (i * len(inputs))}')
        return total_loss


def test():
    correct = 0
    total = len(testset)
    print("evaluating trained model ...")
    with torch.no_grad():
        for i, (names, countries) in enumerate(testLoader, 1):
            inputs, seq_lengths, target = make_tensor(names, countries)
            outputs = classifier(inputs, seq_lengths)
            pred = outputs.max(dim=1, keepdim=True)[1]
            correct += pred.eq(target.view_as(pred)).sum().item()
        percent = '%.2f' % (100 * correct / total)
        print(f'Testset: Accuracy {correct} / {total} {percent}% ')
    return correct / total


if __name__ == '__main__':
    classifier = RNN_GRUClassifier(N_CHARS, HIDDEN_SIZE, N_COUNTRY, N_LAYER)
    if USE_GPU:
        device = torch.device("cuda:0")
        classifier.o(device)
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.Adam(classifier.parameters(), lr=0.001)
    start = time.time()
    print("Training for %d epochs." % N_EPOCHS)
    acc_list = []
    for epoch in range(1, N_EPOCHS + 1):
        # Train cycle
        train()
        acc = test()
        acc_list.append(acc)

    epoch = np.arange(1, len(acc_list) + 1, 1)
    acc_list = np.array(acc_list)
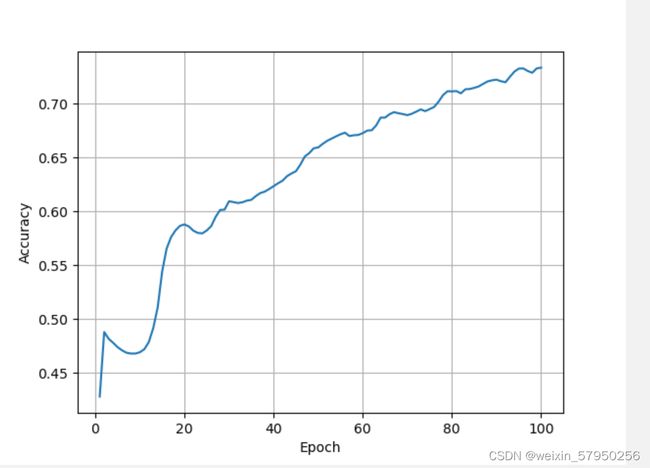
    plt.plot(epoch, acc_list)
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.grid()
    plt.show()

实验结果：