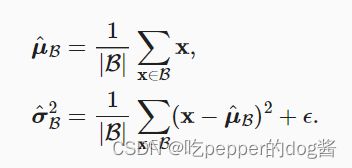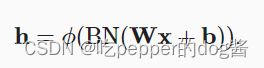训练深层网络

批量规范化的数学表达

批量规范化（batch normalization）在训练深层网络时是一种很好的思路，可持续加速深层网络的收敛速度。

批量规范化的原理是：在每次训练迭代中，首先规范化输入—即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。只有使用足够大的小批量，批量规范化这种方法才是有效且稳定的。

批量规范化根据以下表达式转换x：

 其中：μ^B是小批量B的样本均值，σ^B是小批量B的样本标准差。

拉伸参数（scale）γ和偏移参数（shift）β，它们的形状与x相同。 请注意，γ和β是需要与其他模型参数一起学习的参数。

 全连接层批量规范化

设全连接层的输入为x，权重参数和偏置参数分别为W和b，激活函数为ϕ，批量规范化的运算符为BN。 那么，使用批量规范化的全连接层的输出的计算详情如下

 卷积层批量规范化

我们可以在卷积层之后和非线性激活函数之前应用批量规范化，在每个输出通道的m⋅p⋅q个元素上同时执行每个批量规范化，在计算平均值和方差时，我们会收集所有空间位置的值，然后在给定通道内应用相同的均值和方差，以便在每个空间位置对值进行规范化。、

预测过程中批量规范化

批量规范化在训练模式和预测模式下的行为通常不同，将训练好的模型用于预测时，我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了，一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。

批量规范化层代码实现

batch_normal实现其数学原理

import torch
from torch import nn
from d2l import torch as d2l


def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

BatchNormal实现其功能

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

详情见李沫老师《动手学深度学习》