(一、5NN-QI):序列模型循环神经网络--吴恩达深度学习课程配套笔记
【第一章】神经网络基础
这一篇从神经网络基础到量化投资应用(NN-QO)的第一章的最后一篇RNN。总结一下,第一部分内容主要讲了什么是神经网络,神经网络可以干什么,怎么构建神经网络、怎么优化神经网络、怎么修改神经网络、神经网络主要有哪几类、分别每一类可以做什么,怎么做。这一节主要讲了序列模型,常见的循环网络模型,LTSM和GRU的原理,以及在机器翻译、语音识别方面的应用。
(一,1NN-QI)神经网络与深度学习–吴恩达深度学习课程配套笔记
(一、2NN-QI)改善神经网络–吴恩达深度学习课程配套笔记
(一,3NN-QI)结构化机器学习项目–吴恩达深度学习配套笔记
(一,4NN-QI)卷积神经网络–吴恩达深度学习配套笔记
第五节 循环神经网络
目录:
- 1.循环序列模型
- 2.自然语言处理与词嵌入
- 3.序列模型和注意力机制
1.循环序列模型
循环神经网络常用于我们生活种的序列问题,我们常见的序列问题有:
- Speech recognition
- Music generation
- Sentiment classification
- DNA sequence analysis
- Machine translation
- Videl activity recognition
- Name entity recognition
1.1记号
首先,我们先来看一下循环网络种常用的记号。
- Notation
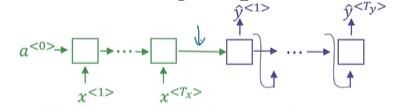
举 例 : H a r r y P o t t e r a n d H e r m i o n e G r a n g e r i n v e n t e d a n e w s p e l l 输 出 : 每 个 名 字 在 本 例 的 中 的 位 置 x < 1 > , x < 2 > . . . x < t > , x < 9 > 表 示 输 入 的 9 个 单 词 , 相 对 应 的 输 出 序 列 表 示 为 : y < 1 > , y < 2 > . . . y < t > , y < 9 > X 表 示 输 入 。 Y 表 示 输 出 。 X ( i ) 表 示 X 的 中 的 第 i 个 样 本 , x ( i ) < t > 表 示 第 i 个 样 本 中 的 第 t 个 分 量 。 T x , T y 分 别 表 示 输 入 和 输 出 序 列 的 长 度 。 在 本 例 中 T x = T y = 9 举例:Harry \ Potter \ and \ Hermione \ Granger \ invented \ a \ new \ spell \\ {}\\ 输出:每个名字在本例的中的位置\\ {}\\ x^{<1>} , \,x^{<2>} ... \,x^{} , \,x^{<9>}\\ {}\\ 表示输入的9个单词,相对应的输出序列表示为:\\ {}\\ y^{<1>} , \,y^{<2>} ... \,y^{ 举例:Harry Potter and Hermione Granger invented a new spell输出:每个名字在本例的中的位置x<1>,x<2>...x<t>,x<9>表示输入的9个单词,相对应的输出序列表示为:y<1>,y<2>...y<t>,y<9>X表示输入。Y表示输出。X(i)表示X的中的第i个样本,x(i)<t>表示第i个样本中的第t个分量。Tx,Ty分别表示输入和输出序列的长度。在本例中Tx=Ty=9} , \,y^{<9>}\\ {}\\ X 表示输入。Y表示输出。\\ {}\\ X^{(i)}表示X的中的第i个样本,x^{(i) }表示第i个样本中的第t个分量。\\ {}\\ T_x,T_y分别表示输入和输出序列的长度。在本例中T_x=T_y=9
现在我们来看一下,语言序列在计算机种是怎么表示的。如果处理语言问题,计算机中会事先存储一个字典.每一个单词在字典中都有对应的位置。然后,序列中的每一个单词用one-hot向量表示,即在对应位置为1,其他位置为0。
比 如 在 例 子 中 H a r r y 这 个 单 词 在 字 典 中 的 位 置 为 367 。 那 么 : x < 1 > T = [ 0 , 0...1 , 0 , . . . 0 ] 其 中 1 的 位 置 为 375 , 选 取 的 字 典 为 轻 量 集 的 字 典 , 长 度 为 10000 , 所 以 x < t > 的 长 度 也 为 10000. 比如在例子中Harry这个单词在字典中的位置为367。那么:\\ {}\\ x^{<1>T}=[0,0...1,0,...0]\\ {}\\其中1的位置为375,选取的字典为轻量集的字典,长度为10000,所以x^{}的长度也为10000. 比如在例子中Harry这个单词在字典中的位置为367。那么:x<1>T=[0,0...1,0,...0]其中1的位置为375,选取的字典为轻量集的字典,长度为10000,所以x<t>的长度也为10000.

1.2 循环神经网络
当处理序列数据的时候为什么不使用标准神经网络呢,因为序列数据前后的数据有信息关联,而且长度不一。用标准神经网络存在的问题:
Problems:
- Inputs,outputs can be different lengths in different examples.
- Doesn’t share features learned across defferent positions of text.
循环神经网络
前 向 传 播 : a < 0 > = 0 ⃗ a < 1 > = g 1 ( w a a a < 0 > + w a x x < 1 > + b a ) ← t a n h R e L U y ^ = g 2 ( w y a a < 1 > + b y ) ← s i g m o i d . . . a < t > = g ( w a a a < t − 1 > + w a x x < t > + b a ) y ^ = g ( w y a a < t > + b y ) 其 中 参 数 w a x 表 示 用 于 a 的 输 出 , 后 面 乘 以 x 的 权 重 。 其 他 w 类 似 。 现 在 简 化 上 述 公 式 : a < t > = g ( W a [ a < t − 1 > , x < t > ] + b a ) y ^ < t > = g ( w y a < t > + b y ) 其 中 , W a = [ w a a ∣ w a x ] 前向传播: a^{<0>}=\vec{0}\\ {}\\ a^{<1>}=g_1(w_{aa}a^{<0>}+w_{ax}x^{<1>}+b_a) \leftarrow tanh \ ReLU\\ {}\\ \hat{y}=g_2(w_{ya}a^{<1>}+b_y) \leftarrow sigmoid\\ {}\\ ... \\ {}\\ a^{
- 基于时间的反向传播
定义代价函数:
L < t > ( y ^ < t > , y ) = − y ^ < t > l o g y ^ − ( 1 − y < t > ) l o g ( 1 − y ^ < t > ) L ( y ^ < t > , y < t > ) = ∑ t = 1 T x L < t > ( y ^ < t > , y < t > ) L^{
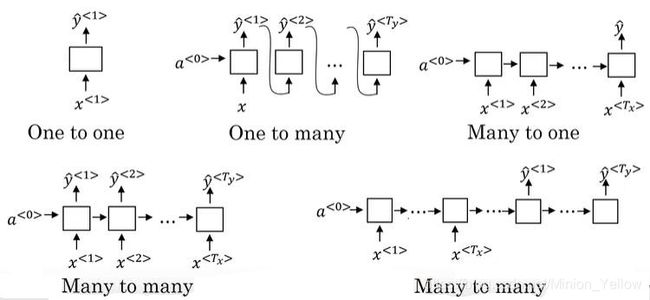
1.3 不同类型的RNNs
上面的这个例子,是一个多对多的例子,常见循环神经网络还有的一对一(标准神经网络),多对一(电影评级),另外一种多对多(机器翻译)。
这些即为常见的循环神经网络结构。
1.4 语言模型和生成序列
例如我们有两句话:
- The apple and pair salad.
- The apple and pear salad.
那么计算机中应该怎么识别这句话呢,在循环神经网络中,这句话就应该为输入,而输出应该为:
- P(The apple and pair salad)
- P(The apple and pear salad)
这便是一个语言处理模型。
现在构建一个RNN语言模型,训练集为一个巨大的语料库。
假如在训练中得到这句话:
Cats average 15 hours of sleep a day.
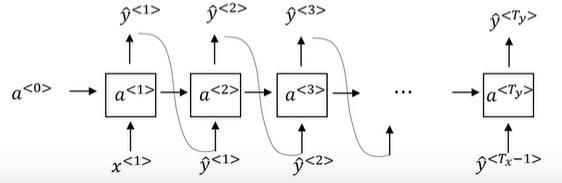
计算机识别这句话,分别每一个单词是个y1,…,y9,我们用多一个向量表示代表句子的结尾。其中每一个向量都是一个one-hot向量,和事先输入的字典做对比,只有在该词的位置上为1其他位置为0.而输出为在之前序列的条件下输出该词的概率,具体结构如下:
1.5 对新序列采样(Sampling novel seuences)
对一个新训练好的模型,我们进行随机采样,采样基于词汇和单词,比如输出的序列y,假如词汇库有10000个词汇,那么每个输入y的分量就有10000个分量。其中每一个分量都为输出该该位置词汇的概率。
1.6 RNNs的梯度消失
在之前的学习中,如果神经网络的层次特别多,在反向传播的过程中,最后的梯度很可能由于层次太多,难以传播到最前面的神经网络层,可能导致梯度消失或者梯度爆炸。这样的问题在循环神经网络中也依然存在。如果处理的序列太长,那么后面输入的信息对前几层的信息影响将会减弱。下面来是几种改善梯度消失的方法。
1.6.1 GRU单元
现在通过一种门控制循环GRU单元,来控制梯度消失的情况。
当 我 们 不 是 用 G R U 单 元 时 : 其 中 的 隐 藏 层 为 : a < t > = g ( w a [ a < t − 1 > , x < t > ] + b a ) 加 上 G R U 单 元 : c ~ < t > = t a n h ( W c [ Γ r ∗ c < t − 1 > , x < t > ] + b c ) Γ u = σ ( W u [ c < t − 1 > , x < t > ] + b u ) Γ r = σ ( W r [ c < t − 1 > , x t ] + b r ) c < t > = Γ u ∗ c ~ < t > + ( 1 − Γ u ) + c < t − 1 > 其 中 c 表 示 记 忆 单 元 , Γ 表 示 遗 忘 单 元 当我们不是用GRU单元时:\\ {}\\ 其中的隐藏层为:\\ {}\\ a^{
1.6.2 LTSM(长短期记忆网络)
- 参考文献【Hochreiter & Schmidhuber 1997. Long short-term memory】
G R U : c ~ < t > = t a n h ( W c [ Γ r ∗ c < t − 1 > , x < t > ] + b c ) Γ u = σ ( W u [ c < t − 1 > , x < t > ] + b u ) Γ r = σ ( W r [ c < t − 1 > , x t ] + b r ) c < t > = Γ u ∗ c ~ < t > + ( 1 − Γ u ) + c < t − 1 > a < t > = c < t > L S T M : c ~ < t > = t a n h ( W c [ a < t − 1 > , x < t > ] + b c ) Γ u = σ ( W u [ a < t − 1 > , x < t > ] + b u ) Γ f = σ ( W f [ a < t − 1 > , x t ] + b f ) Γ o = σ ( W o a < t − 1 > , x t ] + b o ) c < t > = Γ u ∗ c ~ < t > + Γ f ∗ c < t − 1 > a < t > = Γ o ∗ t a n h c < t > GRU:\\ {}\\ \tilde{c}^{}=tanh(W_c[\Gamma_r*c^{ GRU:c~<t>=tanh(Wc[Γr∗c<t−1>,x<t>]+bc)Γu=σ(Wu[c<t−1>,x<t>]+bu)Γr=σ(Wr[c<t−1>,xt]+br)c<t>=Γu∗c~<t>+(1−Γu)+c<t−1>a<t>=c<t>LSTM:c~<t>=tanh(Wc[a<t−1>,x<t>]+bc)Γu=σ(Wu[a<t−1>,x<t>]+bu)Γf=σ(Wf[a<t−1>,xt]+bf)Γo=σ(Woa<t−1>,xt]+bo)c<t>=Γu∗c~<t>+Γf∗c<t−1>a<t>=Γo∗tanh c<t>},x^{ }]+b_c)\\ {}\\ \Gamma_u=\sigma(W_u[c^{ },x^{ }]+b_u)\\ {}\\ \Gamma_r=\sigma(W_r[c^{ },x^{t}]+b_r)\\ {}\\ c^{ }=\Gamma_u*\tilde{c}^{ }+(1-\Gamma_u)+c^{ }\\ {}\\ a^{ }=c^{ } {}\\ {}\\ LSTM:\\ {}\\ {}\\ \tilde{c}^{ }=tanh(W_c[a^{ },x^{ }]+b_c)\\ {}\\ \Gamma_u=\sigma(W_u[a^{ },x^{ }]+b_u)\\ {}\\ \Gamma_f=\sigma(W_f[a^{ },x^{t}]+b_f)\\ {}\\ \Gamma_o=\sigma(W_oa^{ },x^{t}]+b_o)\\ {}\\ c^{ }=\Gamma_u*\tilde{c}^{ }+\Gamma_f*c^{ }\\ {}\\ a^{ }=\Gamma_o*tanh \ c^{ }
其中LSTM单个单元的结构图如图所示:
通过多个LSTM单元相连,可以构造出LSTM的串联结构:
1.7 双向神经网络
来看这样的两句话:
- He said,“Teddy bears are on sale!”
- He said,“Teddy Rossevelt was a great President!”
从前三个单词来看Teddy都有可能是名字,但是明显只有第二句话中Teddy才是人名。
所以只从前向训练这样会丢失信息,双向循环网络(Bidirectional RNN,BRNN)便可以避免这个问题:其主要结构如图:
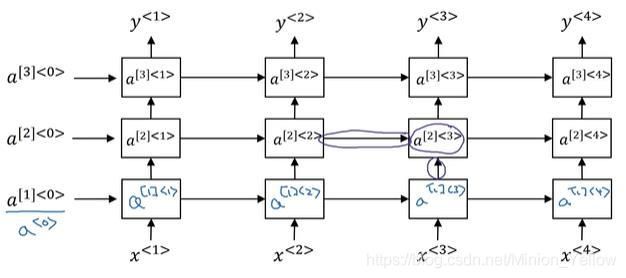
1.8神经循环网络(Deep RNNs)
虽然之前学习了很多深度学习网络模型,但是当学习一个复杂的函数时候我们需要将许多的模型结合起来----深度循环网络。
2.自然语言处理与词嵌入
上一节介绍了GRU,LTSM,DRNN等循环网络框架,这节内容将介绍如何将这些网络模型应用到NLP(自然语处理)问题。
2.1词汇表征
上 节 内 容 介 绍 了 一 个 单 词 在 计 算 机 中 是 怎 么 表 示 的 : 存 在 着 个 “ 词 典 ” V = [ a , a a r o n , . . . , z u l u , < U N K > ] 共 有 10001 个 分 量 , < U N K > 表 示 未 知 词 汇 。 则 : M a n : ( 5391 ) [ 0 0 0 0 ⋮ 1 ⋮ 0 0 ] W o m a n : ( 9853 ) [ 0 0 0 0 0 ⋮ 1 ⋮ 0 ] K i n g : ( 4914 ) [ 0 0 0 ⋮ 1 ⋮ 0 0 0 ] Q u e e n : ( 7157 ) [ 0 0 0 0 0 ⋮ 1 ⋮ 0 ] A p p l e : ( 456 ) [ 0 ⋮ 1 ⋮ 0 0 0 0 0 ] O r a n g e : ( 6257 ) [ 0 0 0 0 0 ⋮ 1 ⋮ 0 ] 上节内容介绍了一个单词在计算机中是怎么表示的:\\ {}\\ 存在着个“词典”V=[a,aaron,...,zulu,
例如Man这个次在V的是第5391个位置的单词,所以Man这个单词就可用上述one-hot向量表示,在第5391位置上的数字是1其他位置上是0.其他的单词也是类似。
但是这样的标记方法,有一个缺陷,任意两个向量的内积都是0,也就是说每个单词和每个单词之间的举例都是0,但是明显Man和woman之间,Apple和Oragne之间更加的类似,所以我们换一种标记方法。
- 词嵌入(word embedding)
| Featrue | Man | Woman | King | Queen | Apple | Orange |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royed | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.7 | 0.69 | 0.03 | -0.02 |
| Food | 0.09 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
通过上面的表格,我们可以用一些特征来表示一个单词如果该单词与该特征相关性越大那么就绝对值就会越大。
假如我们用300个特征来表示一个单词,那么这个单词就可以表示为一个300维的特征向量,如果需要可视化,那么我们把这300维的特征向量映射为2维或3维坐标上的点,如图,之间距离越近,表示单词之间的性质也就越相似。
这种方法叫t-SNE,参考文献【van der Maaten and Hinton., 2008. Visualizing data using t-SNE】
- 应用
通过循环神经网络,我们来学习这句话:
- Sally Johnson is an orange farmer
其中那个单词是人名呢,显然Sally Johnson是人名,为什么呢,因为是orange Farmer一定是一个人。但是我们怎么判断在这句话中:
- Rober Lin is a durian cultivator
人名是哪个单词呢,durian cultivator这是两个不常见的单词,在训练集中甚至没有这两个单词,但是通过大量的数据计算,我们可以发现durian和orange的相似度较近,cultivator和farmer相似度较高,从而判断Robert Lin是一个人名,这就是计算机通过神经网络判断的一个基本逻辑。
其中训练神经网络需要大量的数据,需要到迁移学习,上述的NLP问题应用其实也是一中迁移学习,总结一下词汇嵌入和迁移学习的步骤:
- 1.Learn word embeddings from large text corpus.(1-100B words)
- 2.Transfer embedding to new task with smaller training set.
- 3.Optional:Continue to finetune the word embeddings with new data.
理解
现在我们来进一步理解t-SEN算法,
| Featrue | Man | Woman | King | Queen | Apple | Orange |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royed | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Age | 0.03 | 0.02 | 0.7 | 0.69 | 0.03 | -0.02 |
| Food | 0.09 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
如 果 M a n → W o m a n , 那 么 K i n g → ? , 我 们 可 以 理 解 到 是 Q u e e n , 但 是 怎 么 让 计 算 机 判 断 出 来 呢 ? 我 们 用 e m a n , e w o m a n , e k i n g , e q u e e n 分 别 表 示 4 个 单 词 的 特 征 向 量 。 从 分 析 表 中 , 我 们 可 以 发 现 : e m a n − e w o m a n ≈ [ − 2 0 0 0 ] e k i n g − e q u e e n ≈ [ − 2 0 0 0 ] 所 以 想 要 找 到 q u e e n , 有 : e m a n − e w o m a n ≈ e k i n g − e ? 用 e w 代 替 e ? , 那 么 寻 找 w 的 式 子 为 : w : a r g m a x w s i m ( e w , e k i n g − e m a n + e w o m a n ) 关 于 常 见 的 相 似 函 数 有 : 余 弦 相 似 函 数 : s i m ( u , v ) = u T v ∣ ∣ u ∣ ∣ 2 ∣ ∣ v ∣ ∣ h 如果Man \rightarrow Woman,那么 King \rightarrow?,我们可以理解到是Queen,但是怎么让计算机判断出来呢?\\ {}\\ 我们用e_{man},e_{woman},e_{king},e_{queen}分别表示4个单词的特征向量。从分析表中,我们可以发现:\\ {}\\ e_{man}-e_{woman} \approx \begin{bmatrix} -2 \\ 0 \\ 0 \\ 0 \end{bmatrix} e_{king}-e_{queen} \approx \begin{bmatrix} -2 \\ 0 \\ 0 \\ 0 \end{bmatrix}\\ {}\\ 所以想要找到queen,有:\\ {}\\ e_{man}-e_{woman} \approx e_{king}-e_?\\ {}\\ 用e_w代替e_?,那么寻找w的式子为:\\ {}\\ w:arg\mathop {max}\limits_w sim(e_w,e_{king}-e_{man}+e_{woman})\\ {}\\ 关于常见的相似函数有:\\ {}\\ 余弦相似函数:\\ {}\\ sim(u,v)=\frac{u^Tv}{||u||_2||v||_h} 如果Man→Woman,那么King→?,我们可以理解到是Queen,但是怎么让计算机判断出来呢?我们用eman,ewoman,eking,equeen分别表示4个单词的特征向量。从分析表中,我们可以发现:eman−ewoman≈⎣⎢⎢⎡−2000⎦⎥⎥⎤eking−equeen≈⎣⎢⎢⎡−2000⎦⎥⎥⎤所以想要找到queen,有:eman−ewoman≈eking−e?用ew代替e?,那么寻找w的式子为:w:argwmaxsim(ew,eking−eman+ewoman)关于常见的相似函数有:余弦相似函数:sim(u,v)=∣∣u∣∣2∣∣v∣∣huTv
嵌入矩阵
在我们用反向传播进行学习时,其实我们进行学习的就是嵌入矩阵。
嵌 入 矩 阵 : E = [ a a a r o n … o r a n g e … z u l u < u n k > e 11 e 21 … e j 1 … e 10000 , 1 e 10001 , 1 e 12 e 22 … e j 2 … e 10000 , 2 e 10002 , 1 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ] o r a n g e 是 词 典 中 的 6257 个 单 词 , 所 以 e 6257 可 以 表 示 为 : e 6257 = E × O 6257 其 中 O 6257 = [ 0 0 ⋮ 1 ⋮ 0 ] 是 一 个 o n e − h o t 向 量 , 只 有 在 第 6257 个 位 置 上 的 数 字 是 1 其 他 位 置 是 0 。 所 以 第 j 个 单 词 的 特 征 向 量 可 以 表 示 为 : e j = E × O j 嵌入矩阵:\\ {}\\ E= \begin{bmatrix} a & aaron & \dots &orange & \dots & zulu &
2.2学习词嵌入应用
比如一句话:
- I want a glass of orange juice to go along with my cereal.
现在比如我们想学习juice这个词,那么我们就需要从上下文中的学习。现在有三种方法,可以学习到单词juice。
- 4 words on left&right
- Last 1 word
- Nearby 1 word
2.2.1Word2Vec
Skip-grams
I want a glass of orange juice to along with my cereal
通过这句话我们可以构造一个监督学习。首先选一个内容,然后围绕这个单词选取上下文目标,构成一个数据样本。
| Context | Target |
|---|---|
| Orange | Juice |
| Orange | glass |
| Orange | my |
学习词嵌入模型:
Vocb size = 10000k
C o n t e n t c ( " o r a n g e " ) → T a r g e t t ( " j u i c e " ) o c → E → e c → s o f t m a x → y ^ S o f t m a x : P ( t ∣ c ) = e θ c T e c ∑ j = 1 10000 e θ j T e c θ : p a r a m e t e r a s s o c i a t e d w i t h o u t p u t t L ( y ^ , y ) = − ∑ i = 1 10000 y i l o g y ^ i y 是 一 个 o n e − h a t 向 量 。 Content \ c \ ("orange") \rightarrow Target \ t \ ("juice")\\ {}\\ o_c \rightarrow E \rightarrow e_c \rightarrow softmax \rightarrow \hat{y}\\ {}\\ Softmax:\\ {}\\ P(t|c)=\frac{e^{\theta_c^Te_c}}{\sum_{j=1}^{10000}e^{\theta_j^Te_c}}\\ {}\\ \theta:parameter \ associated \ with \ output \ t\\ {}\\ L(\hat{y},y)=-\sum_{i=1}^{10000}y_ilog\hat{y}_i\\ {}\\ y是一个one-hat向量。 Content c ("orange")→Target t ("juice")oc→E→ec→softmax→y^Softmax:P(t∣c)=∑j=110000eθjTeceθcTecθ:parameter associated with output tL(y^,y)=−i=1∑10000yilogy^iy是一个one−hat向量。
负采样
上节内容中Skip-grams可以帮助我们构造一个监督学习模型,但是会用到大量的加法,这样会导致算法,变得很慢。现在来看另外一种方法负采样(Negative sampling)。
- 定义一个新得监督学习模型
I want a glass of orange juice to go along with my cereal
现在定义一种算法,依然是从这个句子中选取一个Content词,然后从它的前后10个词中选取目标词,剩下的目标词从词典中随机选取。
| Context | word | target |
|---|---|---|
| orange | juice | 1 |
| orange | king | 0 |
| orange | book | 0 |
| orange | the | 0 |
| orange | of | 0 |
x为context和word 而 y为 target。这样构成了训练样本,target为1的样本称之为正样本,而target为0的样本称之为反样本。
k为从字典中选取的样本,k=s-20。
c 为 c o n t e x t , t 为 w o r d , y 为 t a r g e t p ( y = 1 ∣ c , t ) = σ ( θ c T e c ) c 为context,t为word,y为target\\ {}\\ p(y=1|c,t)=\sigma(\theta_c^{T}e_c) c为context,t为word,y为targetp(y=1∣c,t)=σ(θcTec)
这样我们就把一个10000个类别的分类问题转换为了10000个二分类问题,从而大大的提升的速度。
原文参见:【Mikolov et. al.,2013. Distrubuted representation of words and phrases and their compositionality】
GloVe word vectors
这是一种相对简单的算法:
原文参见:【Pennington et., al., 2014,GloVe:Golbal vectors for word representation】
$$
x_{ij}= # \ times \ i \ appears \ in \ context \ of j\
{}\
其中i和j相当于上文中的t和C。\
{}\
minimize:\sum_{i=1}^{10000} \sum_{j-1}^{10000} f(x_{ij})(\theta_{i}Te_{j}+b_i-b_{j}{’}-logX_{ij})^2
$$
情绪分类
情感分类问题即是通过一段话分析出,该句话是对电影的夸奖还是贬低。
其主要结构为:
消除偏见
参考文献:【Boluckbasi et al., 2016. Man is to computer programmer as woman is to homemaker?Debiasing word embedings】
3.序列模型和注意力机制
3.1 序列模型
Seq2Seq
Seq2Seq模型在语音识别和机器翻译方面都有着巨大的应用。
语音翻译,序列模型主要是通过将原文字编码再解码实现机器翻译。

当我们进行语音翻译的时候可能一句话会翻译出多种结果,那么我们需要从中选择最优可能的一种。
a r g m a x y < 1 > , . . . , y < T y > P ( y < 1 > , . . . , y < T y > ∣ x ) \mathop{argmax}\limits_{y^{<1>},...,y^{
3.2 Beam search(集束算法)
通过集束算法去寻找最可能的结果。
- 第一步
集束算法存在着一个参数B,本例子令B=3,即每次挑选出最有可能的3个人,在本例中就是in、Jane、september。
- 第二步
第二步,当网络输出第二单词的时候是建立在第一步的基础上输出的,而第一次选取最有可能的三个单词,在此基础上会有30000种可能的输出。然后再从30000种可能选取前3个目标。
P ( y < 1 > , y < 2 > ∣ x ) = P ( y < 1 > ∣ x ) P ( y < 2 > ∣ x , y < 1 > ) P(y^{<1>},y^{<2>}|x)=P(y^{<1>}|x)P(y^{<2>}|x,y^{<1>}) P(y<1>,y<2>∣x)=P(y<1>∣x)P(y<2>∣x,y<1>)
- 第三步
然后第三步再次按照之前的步骤继续进行。
3.3 改进定向搜索
Length normalization
在 上 一 节 中 的 集 束 算 法 , 其 实 就 是 : a r g m a x y < 1 > , . . . , y < T y > ∏ t = 1 T y P ( y < t > ∣ x , . . . , y < t − 1 > ) 最 大 化 原 式 和 最 大 化 它 的 l o g 形 式 : a r g m a x y < 1 > , . . . , y < T y > ∑ t = 1 T y l o g P ( y < t > ∣ x , . . . , y < t − 1 > ) 但 是 通 过 这 个 公 式 , 会 发 现 这 个 公 式 更 偏 向 选 取 短 的 式 子 , 因 为 每 一 个 概 率 值 都 是 小 于 0 的 , 所 以 更 短 的 式 子 的 概 率 值 会 更 大 。 所 以 我 们 通 过 归 一 化 来 消 除 累 乘 带 来 的 影 响 。 1 T y α ∑ t = 1 T y l o g P ( y < t > ∣ x , . . . , y < t − 1 > ) , α 为 一 个 超 参 数 通 过 α 来 调 节 惩 罚 的 力 度 。 在上一节中的集束算法,其实就是:\\ {}\\ \mathop{argmax}\limits_{y^{<1>},...,y^{
3.4 定向搜索的误差分析
在上节内容中我们了解到集束算法,并不是选出最正确的算法,存在束宽B种可能,所以可能最终得到的结构有误差,但是这种误差是由于解码器(编码器)RNN还是由于集束算法造成的。现在我们来讨论这两种算法。
法 语 : J a n e v i s i t e l ′ A f r i q u e e n s e p t e m b r e 翻 译 的 最 终 结 果 有 : H u m a n : J a n e v i s i t s A f r i c a i n S e p t e m b e r . A l g o r i t h m : J a n e v i s i t e d A f r i c a l a s t S e p t e m b e r . 第 一 种 是 一 个 最 优 的 结 果 , 记 为 : y ∗ , 第 二 种 是 一 个 估 计 的 结 果 记 为 y ^ . 通 过 R N N 可 以 计 算 得 出 P ( y ∣ x ) . 现 在 把 P ( y ∗ ∣ x ) 和 P ( y ^ ∣ x ) . 那 么 可 能 存 在 着 两 种 情 况 : P ( y ∗ ∣ x ) > p ( y ^ ∣ x ) P ( y ∗ ∣ x ) ≤ p ( y ^ ∣ x ) c a s e 1 : P ( y ∗ ∣ x ) > p ( y ^ ∣ x ) B e a m s e a r c h c h o s e y ^ . B u t y ∗ a t t a i n s h i g h t e r P ( y ∣ x ) . C o n c l u s i o n : B e a m s e a r c h i s a t f a u l t 第 一 种 情 况 P ( y ∗ ∣ x ) > p ( y ^ ∣ x ) , 最 优 的 概 率 值 大 于 B e a m 算 法 选 出 来 的 概 率 , 但 是 B e a m 的 作 用 就 是 选 出 最 优 的 概 率 值 对 应 的 y , 所 以 说 明 B e a m 算 法 是 错 误 的 。 c a s e 2 : P ( y ∗ ∣ x ) ≤ p ( y ^ ∣ x ) y ∗ i s a b e t t e r t r n s l a t i o n t h a n y ^ . B u t R N N p r e d i c t e d P ( y ∗ ∣ x ) < p ( y ^ ∣ x ) . C o n c l u s i o n : R N N m o d e l i s a t f a u l t . 第 二 种 情 况 B e a m 算 法 的 概 率 值 比 R N N 的 概 率 值 大 , 说 明 R N N 并 没 有 找 到 最 优 的 y ∗ . 即 问 题 出 在 R N N 方 面 。 法语:Jane \ visite \ l'Afrique \ en \ septembre\\ {}\\ 翻译的最终结果有:\\ {}\\ Human: \ Jane \ visits \ Africa \ in \ September. \\ {}\\ Algorithm: \ Jane \ visited \ Africa \ last \ September.\\ {}\\ 第一种是一个最优的结果,记为:y^{*},第二种是一个估计的结果记为\hat{y}.\\ {}\\ 通过RNN可以计算得出P(y|x).现在把P(y^{*}|x)和P(\hat{y}|x).那么可能存在着两种情况:\\ {}\\ P(y^{*}|x)>p(\hat{y}|x)\\ {}\\ P(y^{*}|x) \leq p(\hat{y}|x)\\ {}\\ case1:P(y^{*}|x)>p(\hat{y}|x)\\ {}\\ Beam \ search \ chose \hat{y}. But \ y^{*} \ attains \ highter \ P(y|x).\\ {}\\ Conclusion: Beam \ search \ is \ at \ fault \\ {}\\ 第一种情况P(y^{*}|x)>p(\hat{y}|x),最优的概率值大于Beam算法选出来的概率,但是Beam的作用就是选出最优的概率值对应的y,所以说明Beam算法是错误的。\\ {}\\ case2:P(y^{*}|x) \leq p(\hat{y}|x)\\ {}\\ y^{*} \ is \ a \ better \ trnslation \ than \ \hat{y}. \ But \ RNN \ predicted \ P(y^{*}|x) < p(\hat{y}|x).\\ {}\\ Conclusion: \ RNN \ model \ is \ at \ fault.\\ {}\\ 第二种情况Beam算法的概率值比RNN的概率值大,说明RNN并没有找到最优的y^{*}.即问题出在RNN方面。 法语:Jane visite l′Afrique en septembre翻译的最终结果有:Human: Jane visits Africa in September.Algorithm: Jane visited Africa last September.第一种是一个最优的结果,记为:y∗,第二种是一个估计的结果记为y^.通过RNN可以计算得出P(y∣x).现在把P(y∗∣x)和P(y^∣x).那么可能存在着两种情况:P(y∗∣x)>p(y^∣x)P(y∗∣x)≤p(y^∣x)case1:P(y∗∣x)>p(y^∣x)Beam search chosey^.But y∗ attains highter P(y∣x).Conclusion:Beam search is at fault第一种情况P(y∗∣x)>p(y^∣x),最优的概率值大于Beam算法选出来的概率,但是Beam的作用就是选出最优的概率值对应的y,所以说明Beam算法是错误的。case2:P(y∗∣x)≤p(y^∣x)y∗ is a better trnslation than y^. But RNN predicted P(y∗∣x)<p(y^∣x).Conclusion: RNN model is at fault.第二种情况Beam算法的概率值比RNN的概率值大,说明RNN并没有找到最优的y∗.即问题出在RNN方面。
3.5Belu得分
在语音识别的过程中,怎么判断这个模型的准确性,与图像识别有区别,一句话可能有多种翻译都是正确的。所以定义一种Belu得分来判别模型的准确性。
F r e n c h : L e c h a t e s t s u r l e t a p i s R e f e r e n c e 1 : T h e c a t i s o n t h e m a t R e f e r e n c e 2 : T h e r e i s a c a t o n t h e m a t M T o u t p u t : t h e t h e t h e t h e t h e t h e t h e 这 是 一 个 法 语 翻 译 为 英 语 的 例 子 , 例 子 中 给 出 了 两 个 参 考 , 这 两 个 参 考 都 是 正 确 的 , M T 为 一 个 极 端 机 器 翻 译 的 结 果 。 现 在 定 义 准 确 度 : P r e c i s i o n : 7 7 M o d i f i e d p r e c i s i o n : 2 7 定 义 准 确 度 : 分 母 为 该 句 子 中 单 词 的 个 数 , 分 子 为 该 单 词 是 否 在 参 考 句 中 出 现 。 以 上 述 翻 译 为 例 , M T 输 出 的 句 子 有 7 个 单 词 , 每 个 单 词 都 在 参 考 句 子 中 有 , 但 是 显 然 这 样 定 义 的 准 确 度 是 不 合 理 的 。 改 正 准 确 度 : 对 于 单 词 t h e , 分 母 表 示 t h e 在 M T o u t p u t 中 出 现 的 次 数 , 分 子 表 示 单 词 t h e 在 每 个 参 考 句 子 中 输 出 的 上 限 值 。 t h e 在 第 一 个 句 子 中 出 现 两 次 , 在 第 二 个 句 子 中 出 现 了 一 次 , 所 以 上 限 为 2 次 , 即 准 确 率 为 2 7 B l e u 得 分 上 述 改 正 准 确 率 为 一 个 单 词 的 , 现 在 我 们 来 看 词 汇 的 准 确 率 怎 么 计 算 。 R e f e r e n c e 1 : T h e c a t i s o n t h e m a t . R e f e r e n c e 2 : T h e r e i s a c a t o n t h e m a t . M T o u t p u t : T h e c a t t h e c a t o n t h e m a t . French: Le \ chat \ est \ sur \ le \ tapis \\ {}\\ Reference 1: The \ cat \ is \ on\ the \ mat\\ {}\\ Reference 2: There \ is \ a \ cat \ on\ the \ mat\\ {}\\ MT \ output : the \ the \ the \ the \ the \ the \ the \\ {}\\ 这是一个法语翻译为英语的例子,例子中给出了两个参考,这两个参考都是正确的,MT为一个极端机器翻译的结果。现在定义准确度:\\ {}\\ Precision: \frac{7}{7} \quad Modified \ precision : \frac{2}{7}\\ {}\\ 定义准确度:分母为该句子中单词的个数,分子为该单词是否在参考句中出现。以上述翻译为例,MT输出的句子有7个单词,每个单词都在参考句子中有,但是显然这样定义的准确度是不合理的。\\ {}\\ 改正准确度:对于单词the,分母表示the在MT output中出现的次数,分子表示单词the在每个参考句子中输出的上限值。the在第一个句子中出现两次,在第二个句子中出现了一次,所以上限为2次,即准确率为 \frac{2}{7} \\ {}\\ Bleu得分\\ {}\\ 上述改正准确率为一个单词的,现在我们来看词汇的准确率怎么计算。\\ {}\\ Reference1:The \ cat \ is \ on \ the \ mat.\\ {}\\ Reference2:There \ is \ a \ cat \ on \ the \ mat.\\ {}\\ MT\ output : The \ cat \ the \ cat \ on \ the \ mat. French:Le chat est sur le tapisReference1:The cat is on the matReference2:There is a cat on the matMT output:the the the the the the the这是一个法语翻译为英语的例子,例子中给出了两个参考,这两个参考都是正确的,MT为一个极端机器翻译的结果。现在定义准确度:Precision:77Modified precision:72定义准确度:分母为该句子中单词的个数,分子为该单词是否在参考句中出现。以上述翻译为例,MT输出的句子有7个单词,每个单词都在参考句子中有,但是显然这样定义的准确度是不合理的。改正准确度:对于单词the,分母表示the在MToutput中出现的次数,分子表示单词the在每个参考句子中输出的上限值。the在第一个句子中出现两次,在第二个句子中出现了一次,所以上限为2次,即准确率为72Bleu得分上述改正准确率为一个单词的,现在我们来看词汇的准确率怎么计算。Reference1:The cat is on the mat.Reference2:There is a cat on the mat.MT output:The cat the cat on the mat.
| v | Count | Count_clip |
|---|---|---|
| the cat | 2 | 1 |
| cat the | 1 | 0 |
| cat on | 1 | 1 |
| on the | 1 | 1 |
| the mat | 1 | 1 |
Count 表示该词组在预测句子中出现的次数,Count_clip表示该词汇在参考句子中的次数。所以该机器翻译输出句子的准确度为:
1 + 0 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 = 4 6 用 公 式 表 示 : P 1 = ∑ u n i g r a m s ∈ y ^ C o u n t c l i p ( u n i g r a m s ) ∑ u n i g r a m s ∈ y ^ C o u n t ( u n i g r a m s ) P n = ∑ n ⋅ g r a m s ∈ y ^ C o u n t c l i p ( n ⋅ g r a m s ) ∑ n ⋅ g r a m s ∈ y ^ C o u n t ( n ⋅ g r a m s ) 假 设 句 子 有 p 1 , p 2 , p 3 , p 4 . C o m b i n e d B l e u s c o r e : B P : exp ( 1 4 ∑ n = 1 4 p n ) \frac{1+0+1+1+1}{2+1+1+1+1} = \frac{4}{6}\\ {}\\ 用公式表示:\\ {}\\ P_1 = \frac{\sum_{unigrams\in \hat{y}}Countclip(unigrams)}{\sum_{unigrams\in \hat{y}}Count(unigrams)}\\ {}\\ P_n = \frac{\sum_{n·grams\in \hat{y}}Countclip(n·grams)}{\sum_{n·grams\in \hat{y}}Count(n·grams)}\\ {}\\ 假设句子有p_1,p_2,p_3,p_4.\\ {}\\ Combined \ Bleu \ score:\\ {}\\ BP: \exp{(\frac{1}{4}\sum_{n=1}^4p_n)} 2+1+1+1+11+0+1+1+1=64用公式表示:P1=∑unigrams∈y^Count(unigrams)∑unigrams∈y^Countclip(unigrams)Pn=∑n⋅grams∈y^Count(n⋅grams)∑n⋅grams∈y^Countclip(n⋅grams)假设句子有p1,p2,p3,p4.Combined Bleu score:BP:exp(41n=1∑4pn)
3.6注意力模型
参考文献【Bahdannau et. al., 2014. Neural machine translation by jointly learning to align and translate】
在我们之前的模型当中,机器翻译的主要结构就是编码器和解码器。
在每次翻译的同时需要将所以的词汇输入进行编码和解码实现机器翻译,这样的结构对于长序列是非常的不友好,所以在尽下长序列翻译时,多加一层注意力权重,这样可以把更多的注意力放在当前需要翻译的部分。
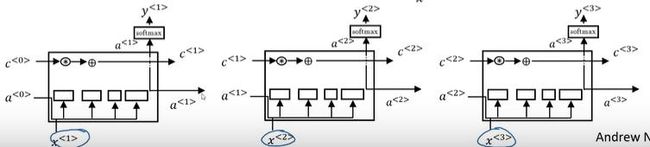
机器翻译,在RNN中每一个都增加一个C向量。用来控制注意力。
C < 1 > = ∑ t ′ α < 2 , t ′ > a < t ′ > a < t , t ′ > = exp ( e < t , t ′ > ) ∑ t ′ = 1 T x exp ( e < t , t ′ > ) C^{<1>}=\sum_{t'}\alpha^{<2,t'>}a^{
参考文献:【Xu et. al., 2015. Show,attend and tell: Neural image eption generation with visual attention】
【总结】
首先向吴恩达教授致敬!
到这里,第一大章神经网络基础完结了,大部分都截屏吴恩达教授的PPT,然后复制他的话,写博客的初衷也就是通过写博客梳理一下自己的逻辑,日后忘记的时候可以回来再看一下,现在感觉又都忘记的差不多。。。。希望接下来对Tensorflow的学习可以更好吧。
这个课程的最后两节是语音识别和关键词唤醒,为什么没有写,因为没看懂…,总之,在全国人民抗疫的同时,自己宅在家,也没事干,花了17天,看完了吴恩达教授4个月的课程,感觉还是比较充实的。
复盘一下,在最开始的时候还是非常有兴趣的,神经网络基础和卷积神经网络这两个章节的内容理解的还比较清晰,但是结构化和RNN的内容中有好多理解的都不是很好,分析一下原因:第一个原因,看的有点快,作业一直没有跟着老师做,所以导致到看后面的内容的时候,对前面内容的记忆就比较模糊。第二个原因,看到最后自己的兴趣就下降了,因为感觉当初学习的初衷就是了解神经网络是什么,然后写学习代码的时候容易些,导致看到最后语音识别的内容不是很感兴趣,所以如果有看到最后不明白的还请见谅,自己移步到b站看原视频。
接下来的安排先把Tensorflow过一遍,相信有吴恩达老师的课程助力,Tensorflow的二刷会更有效果。然后,正真的目的来了,,,(坏笑)做一个关于自己量化投资的项目。如果还有时间和精力,把吴老师的课后作业全部刷一篇。暂时就先计划这样。立个flag(2020年一定要把吴老师的课后作业刷一遍)。
生命不息,学习不止,一起刚八来!