Invertible Denoising Network: A Light Solution for Real Noise Removal
个人论文阅读笔记,可能存在许多瑕疵和错误,欢迎评论指正,谢谢~~
1. 总括
可逆网络在图像去噪方面的优势是在反向传播过程中重量轻、信息无损和节省内存。存在的挑战是输入是有噪声的,而反向输出是干净的,遵循两种不同的分布。本文提出一种可逆去噪网络InvDN,将噪声输入转换为低分辨率清晰图像和包含噪声的潜在表示。为了去除噪声并恢复干净的图像,InvDN在复原过程中用另一个从先验分布中采样的图像来替换噪声潜在表示。(InvDN还能生成与原始表示更相似的噪声)
可逆网络以下三个方面的优势:(1)模型轻,编码和解码使用相同的参数;(2) 它们保留了输入数据的细节,因为可逆网络是无信息损失的;(3) 它们在反向传播期间节省内存,因为无论网络的深度如何,它们都会使用恒定的内存量来计算梯度。因此,可逆模型适用于智能手机等小型设备。
传统可逆模型的原始输入和反向结果遵循相同的分布。相反,对于图像去噪,输入是有噪声的,恢复的图像是干净的,遵循两种不同的分布。因此,可逆去噪网络需要在反向之前去除潜在空间中的噪声。本文提出了一种可逆去噪网络InvDN来解决上述困难。它涉及两个不同的潜在变量;一个包含噪音和高频干净内容,而另一个仅编码干净部分。在前向传播过程中,InvDN将输入图像转换为具有更多通道的缩小的潜在表示。我们训练InvDN使前三个通道的潜在表示与低分辨率清晰图像相同。由于可逆网络保留了输入的所有信息,其余信道中存在噪声信号。为了完全消除噪声,丢弃了所有包含噪声的通道。然而,作为副作用,也丢失了一些与高分辨率清晰图像相对应的信息。为了重建这些缺失的信息,从先验分布中提取一个新的潜在变量,并将其与低分辨率图像相结合,以恢复干净的图像。
本文的贡献:1.本文是第一个为真实图像去噪设计可逆网络的。2.传统可逆网络的潜在变量服从单一分布。相反,InvDN有两个潜在变量,遵循两种不同的分布。因此,InvDN不仅可以恢复干净的图像,还可以生成新的噪声图像。3.InvDN能够生成与原始噪声图像更相似的新噪声图像。
2. Invertible Denoising Network
2.1. Invertible Neural Network
可逆网络最初是为概率模型的无监督学习而设计的。网络可以通过双射函数(bijective function )将一个分布转换为另一个分布,而不会丢失信息。因此,它可以学习观测值的准确密度(exact density)。使用可逆网络,可以通过将遵循简单分布Pz(Z)的给定潜在变量z映射到图像实例x∼Px(X),即x=f(Z)来生成遵循复杂分布的图像,其中f是由网络学习的双射函数。由于双射映射和精确密度估计的性质,可逆网络已成功地应用于图像生成和重新缩放等应用中。
2.2. Challenges in Denoising with Invertible Models
将可逆模型应用于去噪不同于其他应用。在图像生成和重新缩放中广泛使用的可逆网络认为输入和恢复的图像遵循相同的分布。这类应用是可逆模型的直接候选者。而图像去噪则是以一幅含噪图像为输入,重建一幅干净的图像,即输入和恢复的结果服从两种不同的分布。另一方面,可逆变换在变换过程中不会丢失任何信息。然而,图像去噪并不需要具有可逆性的无损特性,因为在将输入图像转换为隐变量时,噪声信息仍然存在。如果我们能够在可逆变换中分离出噪声和干净的信号,就可以重建一幅干净的图像,而不用担心因为放弃了噪声信息而丢失了任何重要的信息。接下来介绍一种通过可逆变换获得干净信号的方法。
2.3. Concept of Design
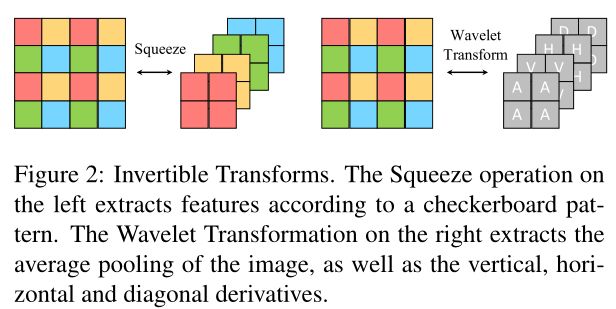
原始噪声图像表示为y,其干净版本为x,噪声为n。有: p(y) = p(x, n) =p(x)p(n|x),利用可逆网络学习到观测值y的潜在表示既包含噪声又包含干净信息。将它们分开很重要。现有的方法通常采用带填充的卷积层来提取特征。然而,由于两个原因,它们是不可逆的:第一,填充使得网络不可逆;第二,卷积的参数矩阵可能不是满秩阵。因此,为了确保可逆性,不使用卷积层,而用可逆特征提取方法,如图2所示的压缩层和Haar小波变换。左侧的压缩操作根据棋盘图案将输入重塑为具有更多通道的特征映射。右侧的Haar小波变换提取原始输入的平均池以及垂直、水平和对角导数。因此,用可逆方法提取的特征地图的空间尺寸不可避免地被缩小。
因此,我们的目标不是直接分离干净的和噪声的信号,而是分离噪声图像的低分辨率和高频分量。采样理论指出,在下采样过程中,高频信号被丢弃。由于可逆网络是信息无损的,如果使变换的潜在表示的前三个通道与下采样的干净图像相同,则高频信息将在其余通道中编码。基于高频信息也含有噪声的观察,我们在反演之前放弃所有的高频表示,从低分辨率分量重建出干净的图像。这一过程描述如下:
其中,![]() 表示低分辨率的清晰图像。我们使用
表示低分辨率的清晰图像。我们使用![]() 来表示
来表示![]() 在重建原始干净图像时无法获得的高频内容。由于将
在重建原始干净图像时无法获得的高频内容。由于将![]() 和n分开是具有挑战性的,因此我们将代表
和n分开是具有挑战性的,因此我们将代表![]() 的所有信道丢弃来完全去除空间变异噪声。然而,副作用是失去了
的所有信道丢弃来完全去除空间变异噪声。然而,副作用是失去了![]() 。为了重建
。为了重建![]() ,我们对
,我们对![]() ∼N(0,i)进行采样,并训练我们的可逆网络来变换
∼N(0,i)进行采样,并训练我们的可逆网络来变换![]() ,并结合
,并结合![]() 来恢复干净的图像x。这样,丢失的高频干净细节
来恢复干净的图像x。这样,丢失的高频干净细节![]() 被嵌入到潜在变量
被嵌入到潜在变量![]() 中
中
3. Network Architecture
首先使用一种有监督的方法来指导网络在变换过程中分离高频和低分辨率分量。在一些可逆变换g之后,噪声图像y被变换成其对应的低分辨率干净图像和高频编码z,即![]() 。最小化以下前向目标
。最小化以下前向目标

其中,![]() 是由网络学习的低频分量,对应于前向传递中的输出表示的三个通道。M是像素数。||·||m是m范数,m可以是1,也可以是2。 为了得到真实的低分辨率图像
是由网络学习的低频分量,对应于前向传递中的输出表示的三个通道。M是像素数。||·||m是m范数,m可以是1,也可以是2。 为了得到真实的低分辨率图像![]() ,通过双三次变换对干净的图像X进行下采样。为了恢复具有
,通过双三次变换对干净的图像X进行下采样。为了恢复具有![]() 的干净图像,使用逆变换
的干净图像,使用逆变换![]() ,其中随机变量
,其中随机变量![]() 是从正态分布N(0,I)中采样的。后向目标写成
是从正态分布N(0,I)中采样的。后向目标写成

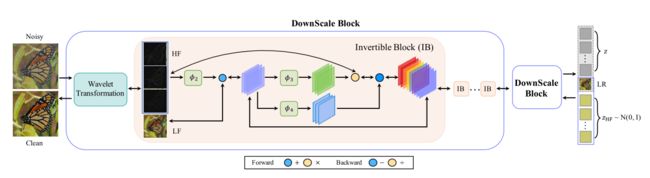
其中x是干净的图像。N是像素数。通过同时利用前向和后向目标来训练可逆变换g。可逆变换g是一个多尺度结构,由几个下尺度块组成。每个向下尺度块由一个可逆的小波变换和一系列的可逆块组成。
3.1. Invertible Wavelet Transformation
目标是在前向通道中学习低分辨率的清洁图像,我们应用了可逆离散小波变换(DWTS),特别是Haar小波变换,来增加特征通道和下采样特征图。在小波变换之后,将输入图像或大小为(H,W,C)的中间特征映射变换为大小为(H/2,W/2,4C)的新特征映射。Haar小波将输入图像分解为垂直、水平和对角方向上的一个低频表示和三个高频表示。
3.2. Invertible Block
每个下尺度块中的小波变换层将表示分解为低频和高频信号,并通过一系列可逆块进行进一步处理。遵循的可逆块是耦合层(coupling layer )。假设块的输入是![]() ,输出是
,输出是![]() 。这个块在前向和反向传播如表一
。这个块在前向和反向传播如表一 
分割(·)操作将大小为(H/2,W/2,4C)的输入特征映射![]() 划分为
划分为![]() 和
和![]() ,分别对应大小(H/2,W/2,C)的低频图像表示和大小(H/2,W/2,3C)的高频特征(如纹理和噪声)。
,分别对应大小(H/2,W/2,C)的低频图像表示和大小(H/2,W/2,3C)的高频特征(如纹理和噪声)。
在表1的R2和R3中,在反向传播过程中,只有加号(+)和乘号(![]() )。运算被反转为减(−)和除(/),而
)。运算被反转为减(−)和除(/),而![]() 、
、![]() 、
、![]() 和
和![]() 执行的运算不要求是可逆的。因此
执行的运算不要求是可逆的。因此![]() 、
、![]() 、
、![]() 和
和![]() 可以是任何网络,包括填充卷积层,由于跳跃连接被证明是深度去噪网络的关键,将R2中的前向操作简化为
可以是任何网络,包括填充卷积层,由于跳跃连接被证明是深度去噪网络的关键,将R2中的前向操作简化为
![]()
这种方法可以将低频特征传递到深层。我们使用残差块作为![]() 、
、![]() 和
和![]() 的操作
的操作
连接(·)是Split(·)的逆操作,它将沿通道的特征映射连接起来,并将它们传递到下一个模块。
完结~~