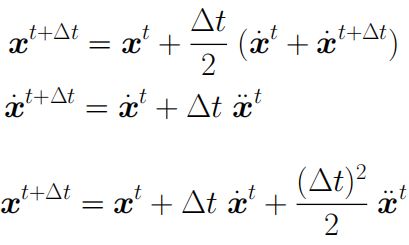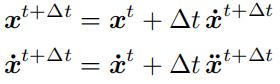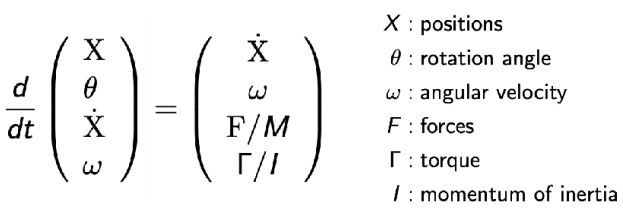Games101-课程22笔记

目录

第二十二节课: 动画与模拟-续集

单粒子模拟

常微分方程 (ODE)

求解粒子位置

欧拉法

        欧拉方法 - 误差

        欧拉方法 - 不稳定性

        两个关键问题

解决欧拉法不稳定的方法

        中点法

        自适应步长

        隐式欧拉法

                如何判断/量化“稳定性”？

        龙格库塔方法

        基于位置/ Verlet 集成

刚体模拟

流体模拟

关键思想

拉格朗日vs欧拉

拉格朗日方法(也叫质点法)

欧拉法(也叫网格法)

材质点方法 (MPM)

---

第二十二节课: 动画与模拟-续集

① 单粒子模拟

• 显式欧拉法

• 不稳定和改进

② 刚体模拟

③ 流体模拟

单粒子模拟

首次研究单个粒子的运动

• 稍后，推广到大量粒子

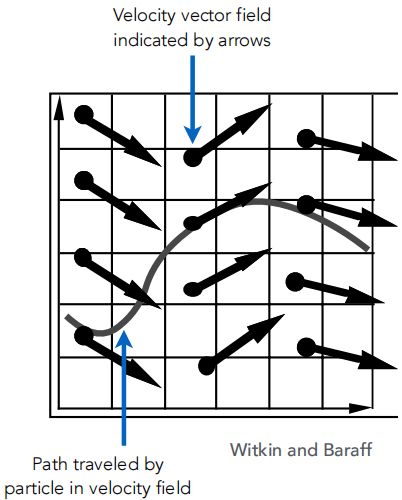
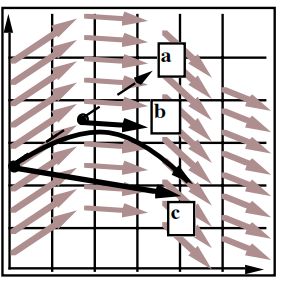
首先，假设粒子的运动由速度矢量场确定，该矢量场是位置和时间的函数：

 

Velocity vector field indicated by arrows: 用箭头表示速度矢量场

Path traveled by particle in velocity field: 粒子在速度场中经过的路径

常微分方程 (ODE)

计算粒子随时间的位置需要求解一阶微分方程：

“一阶”是指所取的一阶导数

“常”表示没有“偏”导数，即 x 只是 t 的函数, 不是常数

 

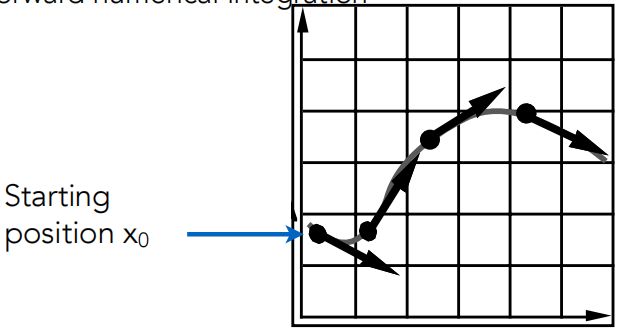
求解粒子位置

在给定初始粒子位置 x0 的情况下，我们可以通过使用正向数值积分来求解 ODE

 

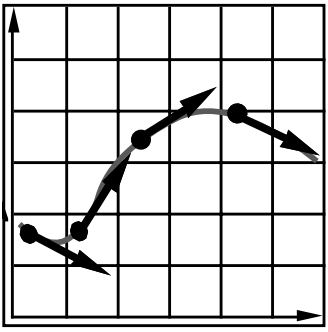
欧拉法

欧拉方法（又名正向欧拉，显式欧拉）

用上一帧的数据(位置,速度,加速度)算出下一帧的数据.

• 简单的迭代方法        • 常用

• 很不准确                   • 常常不稳定

 

欧拉方法 - 误差

通过数值积分，误差会累积,  欧拉积分特别差

Solution path(需要模拟的路线)

Euler estimate with small time step : 步长小        Euler estimate with large time step : 步长大

 (步长)特别小, 越精确模拟.

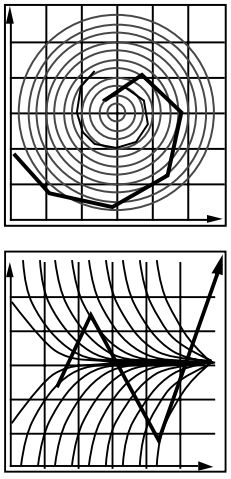
欧拉方法 - 不稳定性

两个关键问题：

① 随着时间步长 Δt 的增加，不准确度也会增加

② 不稳定是一个常见的严重问题，可能会导致模拟出现偏差

通过有限差分数值积分求解, 导致两个问题：

① 误差

• 每个时间步的误差累积。 精度随着模拟的进行而降低

• 精度在图形应用程序中可能并不重要

② 不稳定

• 误差可能会加剧，即使基础系统没有，也会导致模拟出现偏差

• 缺乏稳定性是仿真中的一个根本问题，不容忽视

解决不稳定的方法

① 中点法/修正欧拉

• 起点和终点的平均速度

② 自适应改变步长方法

• 递归比较一步和两个半步，直到可以接受错误

③ 隐式方法

• 在下一个时间步使用速度（困难）

④ 基于位置 / Verlet 集成

• 在时间步之后约束粒子的位置和速度

中点法的具体步骤

• 计算欧拉步骤 (a)

• 计算中点的导数

欧拉步骤 (b)

• 使用中点更新位置

导数 (c)

修正欧拉

• 步骤开始和结束时的平均速度

• 更好的结果

 

 

自适应步长

① 把一个欧拉步长为 分成两个欧拉步长为

② 对前半步和后半步逐一进行欧拉法 ,得出最后的位置, 与一个欧拉步长的最终位置对比

③ 若小于误差阈值则无需继续细分步长, 若大于则继续细分

• 根据误差估计选择步长的技术

• 非常实用的技术

• 但可能需要非常小的步长！

重复直到错误低于阈值：

• 计算 xT 一个欧拉步长，大小为 T

• 计算 xT/2 两个欧拉步长，大小为 T/2

• 计算误差|| xT – xT/2 || , 如果（误差 > 阈值）减小步长并重试

 

 

隐式欧拉法

隐式方法

• 非正式地称为后向方法

• 在当前步骤中使用未来的衍生产品

• 求解和的非线性问题

• 使用寻根算法，例如 牛顿法

• 提供更好的稳定性

如何判断/量化“稳定性”？

• 我们使用局部截断误差（每一步）/总累积误差（整体）

• 绝对值无关紧要，但顺序与步长有关系

• 隐式欧拉的阶数为 1，这意味着

- 局部截断误差：

- 全局截断误差：（h 是步长，即 Δt）

• 对O(h) 的理解

- 如果我们将 h 减半，预期误差也会减半, 那么也就是阶数越高, 越能减小误差

龙格库塔方法

求解 ODE 的一系列高级方法

• 特别擅长处理非线性

• 它的四阶版本是使用最广泛的版本，即 RK4

 

基于位置/ Verlet 集成

思想：

• 修改后的欧拉前步，约束粒子的位置以防止发散、不稳定的行为

• 使用受约束的位置来计算速度

• 这两种想法都会消耗能量，稳定

优点与缺点:

• 快速简单

• 不是基于物理的，无法消耗能量

刚体模拟

简单案例

• 类似于模拟粒子

• 只需考虑更多属性

 

流体模拟

一种简单的基于位置的方法

关键思想

• 假设水由小的刚体球体组成

• 假设水不能被压缩和拉伸（即恒定密度）

• 所以，只要某处的密度发生变化，就应该通过改变粒子的位置来“校正”

• 你需要知道任何地方的每个粒子的位置的密度梯度

• 更新？ 只是梯度下降(机器学习)！

ps: 会出现粒子运动不停止的情况, 因为这是基于位置的方法, 没有能量损失. 所以需要优化方法, 例如加上人为的能量损失.

拉格朗日vs欧拉

模拟大量物体的两种不同视图

拉格朗日方法(也叫质点法)

比如要模拟一群鸟的运动, 对每一只都单独模拟其运动.

 

欧拉法(也叫网格法)

对空间进行网格划分, 在每个时刻的各个网格操作.

如果下图中鸟的位置没有错误: 那么鸟就是倒着飞(相对位置是参照上图), 因为是盯着一个网格查看鸟.

材质点方法 (MPM)

混合的，结合欧拉和拉格朗日观点

• 拉格朗日：考虑携带材质特性的粒子

• 欧拉：使用网格进行数值积分

• MPM：粒子将属性传递给网格，网格执行更新，然后插入回粒子