PyTorch学习笔记（6）损失函数与优化器

这一部分就大写的懵逼，概念好像又懂一点，讲又讲不出来。。。

---

损失函数

L1LOSS

每一个样本经过模型后会得到一个预测值，然后得到的预测值和真实值的差值就成为损失。（当然损失值越小证明模型越是成功）

例如：

当 reduction 为 "sum" 时，求和；

当 reduction 为 "mean" 时，取平均。

代码实现如下：

import torch
from torch.nn import L1Loss

inputs = torch.tensor([1,2,3],dtype=torch.float32)
targets = torch.tensor([1,2,5],dtype=torch.float32)

inputs = torch.reshape(inputs,(1,1,1,3))
targets = torch.reshape(targets,(1,1,1,3))

loss = L1Loss(reduction='sum')
result = loss(inputs,targets)
print(result)
# tensor(2.)

MSELOSS

这个函数的不同之处在于，求差值后会取平方，其余和 L1LOSS 一致。

CROSSENTROPYLOSS

交叉熵，比较复杂，在分类问题中会用到。

import torch
from torch import nn

x = torch.tensor([0.1,0.2,0.3])
y = torch.tensor([1])

x = torch.reshape(x,(1,3))

loss_cross = nn.CrossEntropyLoss()
# 注意输入
result_cross = loss_cross(x,y)

print(result_cross)

优化器

优化器就是在深度学习反向传播过程中，指引目标函数的各个参数往正确的方向更新合适的大小，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小。

想要使用优化器，首先就得弄明白，什么是反向传播与梯度下降？

梯度下降法是通用的优化算法**，反向传播法**是梯度下降法在深度神经网络上的具体实现方式。

• 梯度下降是找损失函数极小值的一种方法。
• 反向传播是求解梯度的一种方法。

很多地方都把梯度下降想象成爬山：

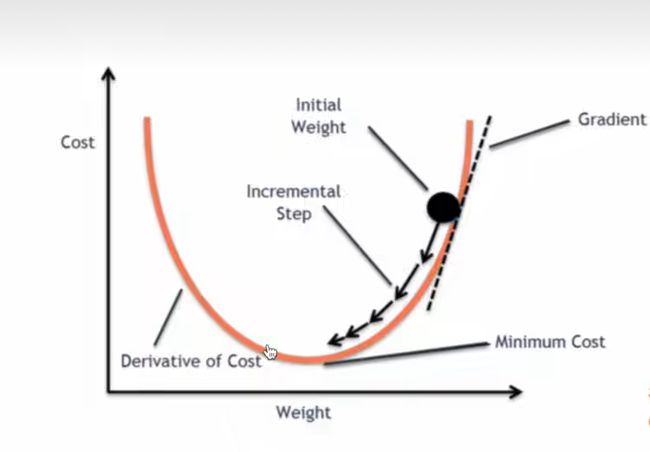
优化的参数为权重和偏置

详情请看：

神经网络中的梯度下降与反向传播的关系

反向传播和梯度下降的关系

优化器(Optimizer)

优化器与损失函数在神经网络的实现如下：

import torch
import torch.nn.functional as F
import torchvision
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
from torch.nn import Conv2d, MaxPool2d, Sigmoid, Flatten, Linear, Sequential
from torch import nn

dataset = torchvision.datasets.CIFAR10("./dataset_CIFAR10",train=False,transform=torchvision.transforms.ToTensor())

dataloader = DataLoader(dataset,batch_size=64)

class Tudui(nn.Module):
    def __init__(self):
        super(Tudui, self).__init__()
        self.model1 = Sequential(
            Conv2d(3, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 64, 5, padding=2),
            MaxPool2d(2),
            Flatten(),
            Linear(1024, 64),
            Linear(64, 10)
        )

    def forward(self, x):
        x = self.model1(x)
        return x


loss = nn.CrossEntropyLoss()
tudui = Tudui()
optim = torch.optim.SGD(tudui.parameters(), lr=0.01)    # 优化器 学习率不能太大，也不能太小，太大不稳定，太小速率过慢
for epoch in range(20): # 训练20轮，不断地降低损失
    running_loss = 0.0
    for data in dataloader:
        imgs, targets = data
        outputs = tudui(imgs)
        result_loss = loss(outputs, targets)
        optim.zero_grad()  # 将每一次的梯度清零，防止对下一次造出干扰
        result_loss.backward() # 调用损失函数的反向传播，求出每次的梯度
        optim.step()    # 对每个参数进行调优
        running_loss = running_loss + result_loss
    print(running_loss)

可以看出，损失值在不断地降低。