Swin-transformer block整体理解
文章目录
- 前言
- 一、整体流程
- 二、自注意力编码
- 三、相对位置编码
- 四、自注意力计算
- 五、总结
- 六、参考链接
前言
上一篇博客中我们概述了Swin-transformer整体框架,这篇博客就来介绍Swin-transformer block,其中包括attention计算,自注意编码与相对位置编码(relative position representation)。
一、整体流程
官方给出的Swin-transformer block的结构如图:

图片链接: https://arxiv.org/pdf/2103.14030.pdf
首先数据执行一次shortcut, 和残差一致,与W-MSA的输出相加得到Źl 。接着通过LN层。LN层就是做一次normalization,以上两部代码如下:
shortcut = x
x = self.norm1(x)
在进入MSA之前,需要做一次数据的填充。因为我们在MSA内要将数据划分为7×7 的窗口,因此数据的W与H维度必须为7的倍数。倘若不满足7的倍数条件,那么就将数据补0成为7的倍数。具体代码如下:
pad_l = pad_t = 0
pad_r = (self.window_size - W % self.window_size) % self.window_size
pad_b = (self.window_size - H % self.window_size) % self.window_size
x = F.pad(x, (0, 0, pad_l, pad_r, pad_t, pad_b))_, Hp, Wp, _ = x.shape #Wp: 238 Hp: 154
MSA层分为两种,W-MAS与SW-MSA。进入W-MAS层时,我们不考虑窗口移动(cyclic shift),也就没有自注意编码操作(attn_mask,这是一个难点,官方库issue 38专门介绍了自注意编码操作,之后我会仔细介绍),具体代码如下:
shifted_x = x
attn_mask = None
但进入SW-MSA层我们需要考虑窗口移动与自注意编码操作,所以要将数据向右移动3格,如下图所示:
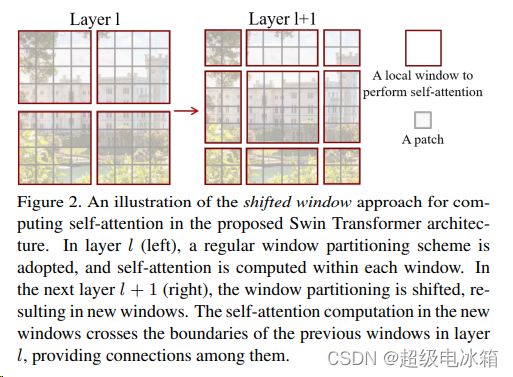
图片链接: https://arxiv.org/pdf/2103.14030.pdf
具体代码如下:
shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
attn_mask = mask_matrix
准备工作完成后,进入MSA层。在MSA层内,首先是将图片切割(window partition)为7×7 的窗口,切割后的维度为[(Hp×Wp)/7×7, 7×7, C]。Hp 是padding过后的H,Wp为padding过后的W,(Hp×Wp)/(7×7)代表77窗口的个数。之后通过一层全连接,将通道数扩大为3倍,数据维度变为[(HpWp)/7×7, 7×7, 3×C],再通过reshape与permute操作将数据维度变为[3, (Hp×Wp)/7×7, 3, 7×7, C/3]。第一个3表示矩阵k, q, v,用于自适应的计算,(Hp×Wp)/(7×7)代表7×7窗口的个数,第二个3表示3个头(heads),应用了多头自注意力机制(multi-head attention),防止过拟合,最后的C/3当然也会是通道数。接下来就是自适应力计算,这个也很复杂,需要理解自注意编码与相对位置编码(relative position representation),所以放到之后介绍。这部分代码如下:
# partition windows
x_windows = window_partition(shifted_x, self.window_size)
# nW*B, window_size, window_size, C
x_windows = x_windows.view(-1, self.window_size*self.window_size, C)
# nW*B, window_size*window_size, C
# W-MSA/SW-MSA
attn_windows = self.attn(x_windows, mask=attn_mask)
# nW*B, window_size*window_size, C
自适应计算完成后,我们要还原数据维度到原始的(B, H, W, C)。还原过程主要就是合并窗口,去掉padding部分,若移动过窗口的话也要逆向移动回去(reverse cyclic shift),还原回初始状态。具体代码:
# merge windows
attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C) # nW*B, window_size, window_size, C
shifted_x = window_reverse(attn_windows, self.window_size, Hp, Wp)
# B H' W' C
# reverse cyclic shift. call back to origin H W
if self.shift_size > 0:
x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
else:
x = shifted_x
if pad_r > 0 or pad_b > 0:
x = x[:, :H, :W, :].contiguous()
x = x.view(B, H * W, C)
MSA层内的大致工作流程原文作者也用一张图形象的表示出来:

图片链接: https://arxiv.org/pdf/2103.14030.pdf
最后加上一开始的残差shortcut,再通过LN层与MLP层即可,其中MLP层是一个基本的多层感应器(Multilayer Perceptron)。具体代码如下:
# FFN
x = shortcut + self.drop_path(x)
x = x + self.drop_path(self.mlp(self.norm2(x)))
drop_path其实就是nn.Identity(),目的在于匹配shortcut的数据维度,无实际意义。
以上就是Swin-transformer block的整体结构理解。其中有3点细节还没有讲解,分别为自注意编码,相对位置编码与自适应计算。接下来会逐一道来。
二、自注意力编码
自注意力编码主要运用在移动窗口的自注意力计算。为什么要引入这个概念,那就要从窗口移动后产生的问题说起。
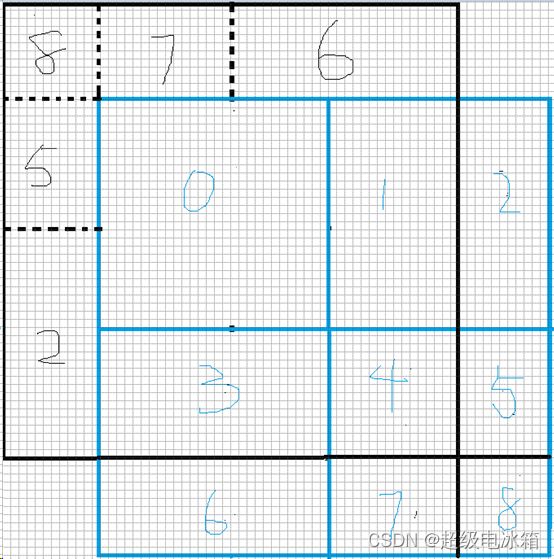
如图所示,特征图从黑色位置移动到蓝色位置,蓝色的0,1,3,4 这4部分与原黑色图重合,但2,5,6,7,8,这5块变多了出来,与原黑色图无直接对应。为此,作者将黑色图也分割出对应得2,5,6,7,8,这5块,使得蓝色图中的每一块特征都可以与黑色原图的特征一一对应。因为自注意力的计算是在7×7的窗口内,所以为了不破快自注意力计算的整体结构,将蓝色1,2放在一个窗口内,蓝色3,6放在一个窗口内,蓝色4,5,7,8放在一个窗口内。这样,在上图内,我们移动后的蓝色特征图同样分成4个7×7的窗口,并可以在窗口内做自注意力计算。但是,问题来了,我们知道自注意力计算只能是数据和其自身,不能是两个不同数据,但由蓝色3,6组成的自注意力窗口中,整体自注意计算时一定会产生3块与6块的注意力计算,如图所示:
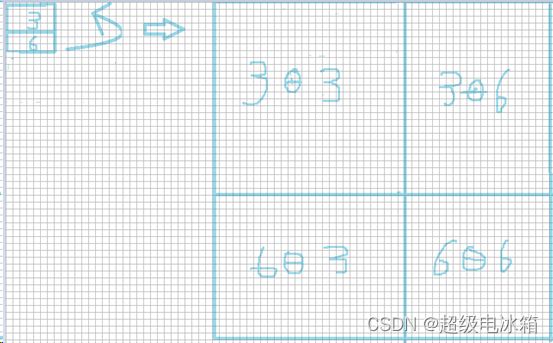
其中3Ɵ3,6Ɵ6是我们所需要的,但是3Ɵ6与6Ɵ3是我们不需要的(Ɵ表示一个运算符号,比如乘法或减法)。同样,将蓝色1,2与蓝色4,5,7,8组成的窗口有着相同的问题。
为了解决这个问题,引入自注意编码。自注意编码的核心思想就是把存在不同数据做自注意的模块直接变为0,比如在蓝色3,6组成的窗户中,我们把3Ɵ6与6Ɵ3这两块的数值变为0即可。将蓝色1,2与蓝色4,5,7,8组成的窗口同理,官方代码库issue38给出了这3块做自注意力产生的图像:

图片链接:
https://github.com/microsoft/Swin-Transformer/issues/38
其中黄色为数据与其本身的自适应,紫色则是不同数据的自适应,需要去除。
在去除方法中,先生成image mask,与图像预处理后的特征图具有相同的维度。接着将这张image mask划分为9个区域,就是我们途中标注的0-8,并将每个区域的数据值赋成区域号。比如0区域的值都是0, 1区域的值都是1,以此类推,再将这个image mask分割成数个7×7窗口,得到mask_windows,维度为[(Hp×Wp)/(7×7), 7×7]。之后通过mask_windows.unsquence(1) - mask_windows.unsquence(2)来得到一个(Hp×Wp/7×7, 7×7,7×7)维度的attn_mask,这个mask内的每一个数值是mask_windows每一个数值与其全部49个值的差。从这个计算可以看出,如果是同区域内的数字相减,值为0,反之不同区域的数值相减不为0。不为0的数据是我们不需要的,直接加-100,变为一个极小的负数,在后续的softmax操作直接将这些极小的负数变为0。具体代码如下:
# Hp, Wp can be divided by window_size 7
Hp = int(np.ceil(H / self.window_size)) * self.window_size #Hp:154
Wp = int(np.ceil(W / self.window_size)) * self.window_size #Wp:238
# create attention mask
img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device) # 1 Hp Wp 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
mask_windows = window_partition(img_mask, self.window_size) # nW, window_size, window_size, 1
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0,
float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
三、相对位置编码
相对位置编码是计算机视觉从自然语言处理引入的概念。在自然语言处理中,一个单词在句子中不同位置出现意思是不同的,比如说I trust what I believe,这里I 出现两次且在句子中做不同成分,不能当成同一个表示,所以要引入相对位置编码。同样在计算机视觉中也可以做类似的理解,比如我们的左手与右手,虽然都是手,但不能当成同一个表示来处理。通过相对位置编码的加入,提高模型的表现。
在7×7的窗口中,下图展示了每一行所有可能产生的相对位置关系:

其中0代表起始点,往左逐一递减,往右逐一递增,与0位置越近其相对值也越接近0。也就是说,只从每一行看,相对位置关系只可能是-6到6中截取的6个连续自然数,相对位置的个数为-6到6,共13个。同理,从每一列看,相对位置关系也为13个。
了解以上概念后,我们要生成一个维度为[13×13,3]的相对偏移表(relative_position_table),13为相对位置个数,3为头个数,要与自注意计算的头个数对应。并使这13×13个相对位置的值满足正态分布,作为相对偏移的权重。代码如下:
# define a parameter table of relative position bias
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) # 2*Wh-1 * 2*Ww-1, nH
trunc_normal_(self.relative_position_bias_table, std=.02)
之后建立一个标准矩阵坐标系coords, coords的结构如下:
[ ( 0 , 0 ) ( 0 , 1 ) ( 0 , 2 ) ( 0 , 3 ) ( 0 , 4 ) ( 0 , 5 ) ( 0 , 6 ) ( 1 , 0 ) ( 1 , 1 ) ( 1 , 2 ) ( 1 , 3 ) ( 1 , 4 ) ( 1 , 5 ) ( 1 , 6 ) ( 2 , 0 ) ( 2 , 1 ) ( 2 , 2 ) ( 2 , 3 ) ( 2 , 4 ) ( 2 , 5 ) ( 2 , 6 ) ( 3 , 0 ) ( 3 , 1 ) ( 3 , 2 ) ( 3 , 3 ) ( 3 , 4 ) ( 3 , 5 ) ( 3 , 6 ) ( 4 , 0 ) ( 4 , 1 ) ( 4 , 2 ) ( 4 , 3 ) ( 4 , 4 ) ( 4 , 5 ) ( 4 , 6 ) ( 5 , 0 ) ( 5 , 1 ) ( 5 , 2 ) ( 5 , 3 ) ( 5 , 4 ) ( 5 , 5 ) ( 5 , 6 ) ( 6 , 0 ) ( 6 , 1 ) ( 6 , 2 ) ( 6 , 3 ) ( 6 , 4 ) ( 6 , 5 ) ( 6 , 6 ) ] \begin{bmatrix} (0,0)&(0,1)&(0,2)&(0,3)&(0,4)&(0,5)&(0,6)&\\ (1,0)&(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)&\\ (2,0)&(2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)&\\ (3,0)&(3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)&\\ (4,0)&(4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6)&\\ (5,0)&(5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)&\\ (6,0)&(6,1)&(6,2)&(6,3)&(6,4)&(6,5)&(6,6)&\\ \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡(0,0)(1,0)(2,0)(3,0)(4,0)(5,0)(6,0)(0,1)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)(0,2)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(0,3)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(0,4)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(0,5)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(0,6)(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
其中括号内左为x,右为y。接着计算每一个坐标与标准矩阵坐标系内全部49个坐标的差值,生成[7×7, 7×7, 2]的相对坐标矩阵(relative_coords),其中2分别代表x与y。在这里,就得到了全部的相对位置(x,y),x∈[-6, 6],y∈[-6, 6]。但问题来了,我们需要通过这个相对位置坐标来对应相对偏移表内的权重值,所以要建立相对位置坐标(x, y)与相对偏移表索引之间一一对应的联系。相对位置偏移表索引为0到13×13,相对位置(x,y)中x∈[-6, 6],y∈[-6, 6],通过公式index = 13*(x + 6) + (y + 6)便可以使相对偏移表索引与相对位置坐标处于同一个值域∈[0, 13×13],满足了一一对应的关系。
有了这一一对应的关系,我们便可以先计算相对位置坐标,转换为对应相对偏移表索引,通过索引得到权重值,成功生成最后的相对位置偏移量矩阵(relative_position_bias)。具体代码如下:
# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w]))
# 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :] # 2, Wh*Ww, Wh*Ww
relative_coords = relative_coords.permute(1, 2, 0).contiguous()
# Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1
# shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1) # Wh*Ww,Wh*Ww,nH
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()
四、自注意力计算
首先我们要理解自注意力计算的公式:
A t t e n t i o n ( Q , K , V ) = S o f t m a x ( Q K T d + a t t e n m a s k + r e l a p o s i n m a s k ) Attention(Q,K,V) = Softmax(\frac{QK^T}{\sqrt{d}} + atten_{mask} + rela_{posin_{mask}}) Attention(Q,K,V)=Softmax(dQKT+attenmask+relaposinmask)
其中Q,K,V分别为3个维度为[1, (Hp× Wp)/7× 7, 3, 7×7, C/3]的输入,其实就是输入x的3个线性形变,d为C/3, 指通道个数,atten_mask为自注意力编码,rela_posin_mask为相对位置编码。
我们知道向量点积的值可以表示特征与特征之间的相似性,那么向量自身每一行特征与自身另一特征的点积的和,可以表示不同特征之间的相似性,也就是特征与特征之间的权重,通过 Q K T QK^T QKT得到,如图:

生成的这个49×49矩阵就是自注意特征权重图。
之后除以√d,是为了缩小矩阵值的范围,让softmax后的值方差尽量小,增强梯度的稳定性。加上自注意力编码是为了给特征权重图增加限制,使其满足移动窗口的特殊要求。当然,如果窗口不移动,自注意力编码为空。再加上相对位置编码,让特征权重图每一个特征都具有相对位置的特殊性。最后通多softmax函数,既保证了权重的非负性(之前提到的注意力编码中的-100,softmax后这部分变为0,满足不同区域做自适应力结果为0),也增加了模型的非线性,得到完整的自注意权重图attn。
得到注意权重图后,通过attn * V,计算出最终的attention结果。再通过Linear层与dropout层,得到最终输出。整体代码如下:
qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4) #(3, 748, 3, 49, 32)
q, k, v = qkv[0], qkv[1], qkv[2] # make torchscript happy (cannot use tensor as tuple)
q = q * self.scale
attn = (q @ k.transpose(-2, -1))
attn = attn + relative_position_bias.unsqueeze(0)
if mask is not None:
nW = mask.shape[0]
attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
attn = attn.view(-1, self.num_heads, N, N)
attn = self.softmax(attn)
else:
attn = self.softmax(attn) #(748, 3, 49, 49)
attn = self.attn_drop(attn)
x = (attn @ v).transpose(1, 2).reshape(B_, N, C) #(748, 49, 96)
x = self.proj(x)
x = self.proj_drop(x)
五、总结
以上结合代码概括了swin-transformer block的整体流程,其中包括自注意编码,相对位置编码与自注意计算流程等一些细节。当然,整体网络框架中肯定还有一些没有讲到或讲的不清楚的地方,今后会做出补充。
六、参考链接
https://github.com/microsoft/Swin-Transformer/issues/38
https://arxiv.org/pdf/2103.14030.pdf
沐神论文精读之swin-transformer