你好,语义分割(一)
摘要
语义分割(Semantic Segmentation),是计算机视觉中的一项关键技术之一,用于识别图像中的对象,并为对象进行分类。从宏观上来看,语义分割为人工智能模拟人类“看得见“的能力提供了基础支撑,为机器对周边场景的理解铺平了道路。本文使用Pytorch框架,实现了一个简单的语义分割模型,并介绍了语义分割技术在实际中的一些应用。旨在通过简单易懂的代码实现,来了解语义分割技术和机器学习的主要开发流程。文章内容涉及了机器学习开发流程中的数据处理,建模和模型评估部分。文章中使用到的流程和算法同样适用于大部分机器学习应用。
【关键词】:语义分割,全卷积神经网络,计算机视觉,人工智能
1. 背景知识
1.1. 语义分割
语义分割(Semantic Segmentation),是计算机视觉中的一项技术,用于识别图像中的对象,并为对象进行分类。语义分割对输入图像中的每一个像素进行处理,并将其划分为特定的分类。在同一幅图像中,相同的对象会被划分为相同的分类。比如下图中的图像,经过语义分割后被划分为不同的区域,以及每个区域对应的语义。
- 语义识别:对图像中的每一个像素进行分类
- 目标定位:识别物体边界
- 语义分割:生成分割标签
1.2. 全卷积神经网络
全卷积神经网络(Fully Convolutional Networks,FCN)[1],是一种特殊的卷积神经网络模型,在2015年由Long等人在“Fully Convolutional Networks for Semantic Segmentation“论文中提出,主要用于处理语义分割问题。全卷积神经网络中的每一层都由一个三维数组组成,形状为H × W × D。其中H为图层的高度,W为图层的宽度,D是图层的维度或者特征。在全卷积神经网络中,使用卷积层取代了传统神经网络的全连接层,使得整个网络模型的参数变得更少,训练速度更快。同时由于去除了全连接层,使得全卷积神经网络可以处理任意大小的输入图像。
全卷积神经网络中使用的主要技术包含:卷积化(Convolutional),跨步卷积(Strided Convolution),跃层连接(Skip Layer),下采样(Downsampling,即卷积神经网络中的池化)和上采样(Upsampling)。
全卷积神经网络通过多次下采样操作,把图像大小缩放为原始图像大小的1/32,由于下采样过程中会产生数据丢失,导致解码后的结果精度不足。针对此问题,全卷积神经网络的打分策略,分为直接打分,联合使用上一次下采样结果打分,和联合使用上两次下采样结果打分的策略,分别被称为 FCN-32s, FCN-16s和FCN-8s。其中FCN-8s由于使用了前两次下采样的数据,所以最终预测的结果的精度通常优于FCN-16s和FCN-32s。

2. 语义分割实现
2.1. 数据(Data)
“数据和特征,决定了机器学习的上限,而模型和算法只是去逼近这个上限而已”
数据是大部分人工智能技术应用的基础,数据处理是人工智能应用中极具挑战的环节。在语义分割中,由于图像自身的特征比较简单,且本文中使用到的图像和标签已经是处理过的,所以只涉及到了一些简单的数据处理流程。
2.1.1. 数据集(Dateset)
Pytorch使用NCHW格式的数据。其中N是批处理数量,C是通道数,H和W表示高度和宽度,所有输入数据需要具有相同的C,H和W。
在Pytorch中,提供了Dataset和DataLoader来辅助处理并生成符合要求的输入数据。为了读取我们用于语义分割的图片和标签数据,我们需要实现自定义数据集来提供数据源。
在我们的自定义数据集中,我们需要重写__len__方法,用来返回数据集的数据数量,同时重写__getItem__方法,用来返回图像数据和标签数据。
class CoalsDataset(Dataset):
def __init__(self, root: str, colors: Tensor, transform=None):
self.root = root
self.colors = colors
self.transform = transform
self.data_list = np.load(f'{root}/index.npy')
def __len__(self):
return len(self.data_list)
def __getitem__(self, index) -> T_co:
names = self.data_list[index]
image_file_path = f'{self.root}/{names[0]}'
mask_file_path = f'{self.root}/{names[1]}'
image = torchvision.io.read_image(image_file_path, ImageReadMode.RGB)
mask = torchvision.io.read_image(mask_file_path, ImageReadMode.RGB)
if self.transform is not None:
image = self.transform(image)
mask = self.transform(mask)
mask = OneHotEncoder.encode_mask_image(mask, self.colors)
return image, mask
这里面有一些细节需要我们注意下:
- pytorch输入需要的图片Tesnsor形状是(N,C,H,W),其中N由数据加载器来生成,所有自定义数据集需要返回(C,H,W)形状的图像数据。一些其它的库,比如matplot,在显示图像时,需要的数据的形状是(H,W,C)。在不同的框架中使用图像数据时,需要关注其要求的输入格式。
- 如果使用其它库来读取图像数据,比如opencv或者Python自身的Image库,需要注意返回数据的形状及不同维度代表的含义。比如opencv返回的图像数据的形状是(H,W,
C),且C是BGR模式(PIL是RGB模式)。在使用数据之前,可能需要我们对图像数据做合适的转换。RGB模式或者BGR模式本身并不影响模型训练和预测,但我们需要关注我们使用的其它工具对通道模式的要求。
2.1.2. one-hot 编码
直接读取的标签图像的数据,是无法用于损失计算的,我们需要把它编码成机器学习模型能够识别的数据。
one-hot编码,是一种公平的编码方法。它把数据编码成仅由二进制0和1组成的向量。对于一个特定的分类,one-hot编码选定其中一个位置设置为1,其它位置均设置为0。对于我们的图像数据来说,编码后的数据的形状是(C,H,W),其中C表示分类的个数(不同于原始图像中用来保存RGB三个通道),H和W和输入图像相同。对于标签图像中的每一个像素,在C维度上表现为[0, 0, 1, 0, 0]的形式,其中像素真实的分类所在列赋值1,其它列的值均为0。
class OneHotEncoder():
@staticmethod
def encode_mask_image(mask_image: Tensor, colors: Tensor) -> Tensor:
height, width = mask_image.shape[1:]
one_hot_mask = torch.zeros([len(colors), height, width], dtype=torch.float)
for label_index, label in enumerate(colors):
one_hot_mask[label_index, :, :] = torch.all(mask_image == label[:, None, None], dim=0).float()
return one_hot_mask
@staticmethod
def encode_score(score: Tensor) -> Tensor:
num_classes = score.shape[1]
label = torch.argmax(score, dim=1)
pred = F.one_hot(label, num_classes=num_classes)
return pred.permute(0, 3, 1, 2)
2.1.3. 数据标准化(Data Normalization)
原始的图像数据,并不总是能符合模型要求的数据的标准,我们需要对原始输入数据进行预处理。如果输入的图片大小不一致,或者图片过大,那么我们需要对原始图像数据进行缩放和裁剪。下面的转换代码,可以把原始图像缩放到224X大小,再中心裁剪得到224224大小。
transform = T.Compose([
T.Resize(224),
T.CenterCrop(224)
])
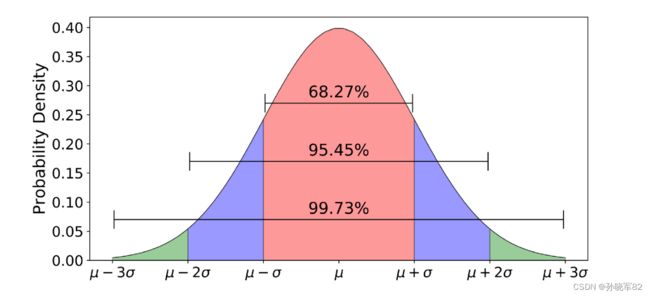
正态分布(Normal Distribution),也称为高斯分布(Gaussian Distribution),是统计学中对数据的连续概率分布规则的定义。当数据特征中存在单位差异,或者输入数据中存在较大的数据时,需要对数据进行标准化处理,用于消除不同单位的数据给算法带来的偏见。即使没有单位差异或较大的输入数据时,标准化的数据,在训练时也更容易收敛,不容易产生过拟合现象。
torchvison提供的Normalize方法实现了Z-Score标准化。其计算公式为:
z n o r m = x − m e a n s t d z_{norm} = \frac {x - mean} {std} znorm=stdx−mean
其中,x表示输入数据,mean表示训练数据的均值,std表示训练数据的标准差。标准化后数据z均值为0,方差为1,符合正态分布标准。
对于均值和标准差的获取,可以采用如下几种方式:
- 如果数据是已知数据集(e.g. COCO),使用数据集提供的均值和标准差
- 对数据集中的所有数据,计算其均值和标准差
- 首先对数据集中的数据进行归一化处理,之后均值和标准差均使用固定值0.5
这里我们采用第三种方式来进行标准化处理。
transform = T.Compose([
T.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
input = transform(input/255.)
2.1.4. 数据加载器(DataLoader)
训练机器学习模型通常需要大量的数据,把这些数据一次性加载到内存中来使用需要占用大量的内存,甚至可能无法完成。
pytorch 使用数据加载器来(DataLoader)来管理数据集,数据加载器不会加载数据集中的所有数据,而是在真正读取数据时,根据批处理大小,使用数据集获取一批次数据来进行处理。
通常完整的数据集会被分组成训练集,验证集和测试集三部分。其中训练集用来学习参数,验证集用来校验模型并调整超参数,测试集用来评估模型。对于小规模样本集(数据量在万级以下),训练集,验证集和测试集可以按6 : 2 : 2的比例来划分。对于大规模样本集,只要保留足够的验证集和测试集即可。
data_len = len(dataset)
indices = list(range(data_len))
split1 = int(data_len * 0.6)
split2 = int(data_len * 0.8)
train_indices, val_indices, test_indices = indices[:split1], indices[split1:split2], indices[split2:]
train_data = Subset(dataset, train_indices)
val_data = Subset(dataset, val_indices)
test_data = Subset(dataset, test_indices)
BATCH_SIZE = 4
NUM_WORKERS = 4
train_loader = DataLoader(
train_data,
BATCH_SIZE,
shuffle=True,
drop_last=True,
num_workers=NUM_WORKERS,
pin_memory=True,
)
val_loader = DataLoader(
val_data,
BATCH_SIZE,
shuffle=False,
drop_last=True,
num_workers=NUM_WORKERS,
pin_memory=False,
)
test_loader = DataLoader(
test_data,
BATCH_SIZE,
shuffle=False,
drop_last=True,
num_workers=NUM_WORKERS,
pin_memory=False,
)
2.1.5. 交叉验证(Cross Validation)
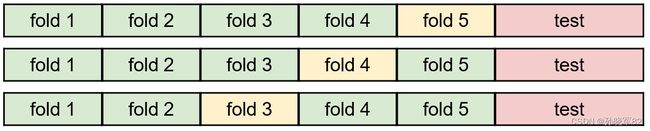
如果样本集规模很小,在样本集拆分后,用于训练和验证的数据规模变得更小,不利于模型训练。K-fold交叉验证把样本数据分成k份,并选择其中一份用作验证,其它用作训练。之后再选择另一份用作验证,如此循环指定的次数或者全部fold都被作为验证集训练过。交叉验证在一定程度上相当于扩充了训练集和验证集的数据量,降低了小规模样本带来的过拟合问题,从而更好地进行模型训练。当样本数量较大时,通常不需要使用交叉验证。
2.2. 模型(Model)
对于初学者来说,往往对晦涩复杂的建模流程望而生畏。其实通常的机器学习应用,建模流程远比想象中简单得多。对于一个特定的人工智能任务,复杂的模型往往是从已知模型中来选择并调整得来,训练过程也通常是一个固定得模式。至于其内部的原理,我们不妨先让它运行起来再慢慢了解不迟。
2.2.1. 模型设计
模型设计是机器学习中的重要内容之一,也是其中较为复杂的部分。对于初学者来说,可以选择先从简单的前馈神经网络,线性回归,逻辑回归等模型来逐渐了解模型设计。
不要纠结于代码中大量出现的字面值常数。在非人工智能开发中,这些数字通常被称为魔数,是代码不规范的表现。在机器学习中,这些常数被称为超参数(Hyperparameter),用来标识在模型训练过程中不参与学习的参数。
我们的FCN-8s模型使用到了卷积(Conv2d),激活函数(ReLU),下采样(MaxPool2d)和上采样(ConvTranspose2d)几种常见的算法和操作。
class FCN8s(nn.Module):
def __init__(self, num_classes):
super(FCN8s, self).__init__()
self.num_classes = num_classes
# 第一层卷积
self.layer1 = nn.Sequential(
nn.Conv2d(3, 48, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(48, 48, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, stride=2, ceil_mode=True) # Downsampling 1/2
)
# 第二层卷积
self.layer2 = nn.Sequential(
nn.Conv2d(48, 128, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(128, 128, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, stride=2, ceil_mode=True) # Downsampling 1/4
)
# 第三层卷积
self.layer3 = nn.Sequential(
nn.Conv2d(128, 192, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(192, 192, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, stride=2, ceil_mode=True) # Downsampling 1/8
)
# 第四层卷积
self.layer4 = nn.Sequential(
nn.Conv2d(192, 256, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(256, 256, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, stride=2, ceil_mode=True) # Downsampling 1/16
)
# 第五层卷积
self.layer5 = nn.Sequential(
nn.Conv2d(256, 512, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(512, 512, (3, 3), padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, stride=2, ceil_mode=True) # Downsampling 1/32
)
# 第六层使用卷积层取代FC层
self.score_1 = nn.Conv2d(512, num_classes, (1, 1))
self.score_2 = nn.Conv2d(256, num_classes, (1, 1))
self.score_3 = nn.Conv2d(192, num_classes, (1, 1))
# 使用反卷积实现上采样
self.upsampling_2x = nn.ConvTranspose2d(num_classes, num_classes, (4, 4), (2, 2), (1, 1), bias=False)
self.upsampling_4x = nn.ConvTranspose2d(num_classes, num_classes, (4, 4), (2, 2), (1, 1), bias=False)
self.upsampling_8x = nn.ConvTranspose2d(num_classes, num_classes, (16, 16), (8, 8), (4, 4), bias=False)
self._initialize_weights()
}
…
}
卷积和反卷积操作,是神经网络中涉及到的较为复杂的操作,需要我们后续做进一步深入了解。这里为了加速模型训练,我们普遍调小了模型相关超参数的取值。
减少通道数量
在全卷积神经网络模型中,每一个卷积层的通道数量,从96增加到 4096,示例模型的通道数量范围从48到256,整体通道数量上比全卷积神经网络模型要小很多。通道数量会影响到权重参数的数量,进而影响模型的训练速度。我们降低了通道数量,获得了更快的训练速度,同时由于减少了通道数量,导致卷积层的感受野变小,预测的精度会有一定程度的降低。
减少卷积层数量
在基于全卷积神经网络的模型中,无论是ResNet还是VGG,在每一个下采样之前,都有多个卷积层,我们的模型每一个下采样前只有二个卷积层。带来的影响同样是提升了训练速度,降低了预测的精度。
去除首次卷积的100单位填充
在大多数全连接神经网络模型中,第一个卷积层通常给定100单位的填充。
我们先看下卷积输出的计算公式:
W o u t = ( W i n – k e r n e l + 2 ∗ p a d d i n g ) / s t r i d e + 1 W_{out} = (W_{in} – kernel + 2 * padding) / stride + 1 Wout=(Win–kernel+2∗padding)/stride+1
其中Wout是卷积后输出的大小,Win是输入大小, kernal是卷积核大小,padding是填充大小,stride是卷积步长。
在第五层卷积后,输出的大小Wout = Win / 32, 接下来的卷积层通常采用大卷积核(比如7)来进行打分,那么根据卷积输出大小的计算公式,输出结果为Wout = Win / 32 – 7 + 1 = (Win -192)/32, 此时如果原始图像大小小于192,那么将导致打分函数无法计算。而首次Pading设置为100,打分之前的输出结果会变成(Win + 2*100 – 2) / 32, 打分的输出也变成了Wout = (Win + 6)/32, 此时原始图像大小不受限制,但同时也引入了过多的噪声,导致预测的精度有所下降。
为了简化,我们在打分卷积层使用了1X1大小的卷积核,那么打分的输出就变成了Wout = Win /32 -1 + 1 = Win / 32, 此时没有原始图像大小受限制的问题,但由于卷积核变小降低了感受野,预测的精度会有所下降。
反卷积实现上采样
为了在FCN-8s网络中,联合前两次下采样的结果来进行打分,我们需要对下采样后的结果进行上采样操作来进行恢复。反卷积是实现上采样操作的一个好的方案。
反卷积计算公式是卷积计算公式的反函数,额外多出了一个output_padding 参数:
Wout = (Win - 1)* stride + kernal - 2 * padding + output_padding
我们对照模型中的upsampling_2x反卷积层中的参数来看:
Wout = ( Win - 1) * 2 + 4 - 2 * 1 + 0 = 2 * Win - 2 + 4 – 2 = 2 * Win
输出大小正好放大到了输入大小的2倍。
2.2.2. 权重初始化
在机器学习中,设置合适的权重初始值非常重要。如果权重参数初始值设置不当,在反向传播(backward)时很容易产生梯度消失或梯度爆炸问题,导致模型训练无法进行。
对于神经网络来说,开发语言中对于浮点数赋予的默认值0,并不适合做权重参数的初始值,我们需要为权重参数赋予合适的初始值。如果网络模型是已知的模型,比如VGG或ResNet,那么通常使用预训练好的参数来初始化默认权重值,我们使用了自己修改的网络模型,所以这里对权重做了手工初始化。
class FCN8s(nn.Module):
…
@staticmethod
def bilinear_kernel(in_channels, out_channels, kernel_size):
factor = (kernel_size + 1) // 2
if kernel_size % 2 == 1:
center = factor - 1
else:
center = factor - 0.5
og = np.ogrid[:kernel_size, :kernel_size]
channel_filter = (1 - abs(og[0] - center) / factor) * \
(1 - abs(og[1] - center) / factor)
weight = np.zeros((in_channels, out_channels, kernel_size, kernel_size),
dtype=np.float64)
weight[range(in_channels), range(out_channels), :, :] = channel_filter
return torch.from_numpy(weight).float()
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
torch.nn.init.xavier_uniform_(m.weight)
if m.bias is not None:
m.bias.data.zero_()
if isinstance(m, nn.ConvTranspose2d):
assert m.kernel_size[0] == m.kernel_size[1]
initial_weight = self.bilinear_kernel(
m.in_channels, m.out_channels, m.kernel_size[0])
m.weight.data.copy_(initial_weight)
…
}
对于卷积层的权重初始化,使用了Xavier初始化方式,反卷积层的权重初始化采用了双线性插值(Bilinear interpolation)算法。激活函数和下采样算法没有权重参数,不需要做权重初始化。
2.2.3. 前向计算(Forward)
前向计算(forward)和反向传播(backward),是模型训练中非常重要的两个组成部分。对于给定的输入,前向计算通过模型进行推理,为输入进行打分。
在前向计算中,下采样后再使用上采样来恢复原始大小可能存在问题。假设我们有一个大小为5的输入,下采样后的大小会变成3,上采样后,大小则变成了6。经过一轮下采样和上采样,输出的大小发生了变化。
为了避免这个问题,我们需要在上采样后,对Tensor进行必要的裁减,使得大小不能被2整除的输入,在一轮下采样和上采样后,能够恢复原来的大小。
class FCN8s(nn.Module):
…
def forward(self, x: torch.Tensor) -> torch.Tensor:
h = self.layer1(x)
h = self.layer2(h)
s1 = self.layer3(h) # 1/8
s2 = self.layer4(s1) # 1/16
s3 = self.layer5(s2) # 1/32
s3 = self.score_1(s3)
s3 = self.upsampling_2x(s3)
s2 = self.score_2(s2)
s2 = s2[:, :, :s3.size()[2], :s3.size()[3]]
s2 += s3
s2 = self.upsampling_4x(s2)
s1 = self.score_3(s1)
s1 = s1[:, :, :s2.size()[2], :s2.size()[3]]
score = s1 + s2
score = self.upsampling_8x(score)
score = score [:, :, :x.size()[2], :x.size()[3]]
return score
…
}