GAMES101-现代计算机图形学入门-闫令琪——Lecture 13 Ray Tracing 1(Whitted-Style Ray Tracing) 学习笔记
Lecture 13 Ray Tracing 1(Whitted-Style Ray Tracing)
Why Ray Tracing?
-
Rasterization couldn’t handle global effects well
--(Soft) shadows
--And especially when the light bounces more than once

-
Rasterization is fast, but quality is relatively low

-
Ray tracing is accurate, but is very slow
-- Rasterization: real-time, ray tracing: offline
--~10K CPU core hours to render one frame in production

(一)、Basic Ray-Tracing Algorithm
1、Light Rays
Three ideas about light rays
①.Light travels in straight lines (though this is wrong) 光沿直线传播
②.Light rays do not “collide” with each other if they cross (though this is still wrong) 两束光相交不会互相产生影响
③.Light rays travel from the light sources to the eye (but the physics is invariant under path reversal - reciprocity). 光线从光源出发最终到人的眼睛中
2、Ray Casting
①、Generate an image by casting one ray per pixel
②、Check for shadows by sending a ray to the light

首先我们要做光线投射,假设我们在往一个虚拟的世界看,面前放了一块成像的屏幕,屏幕被我们划分成了像素格子。对于每一个像素从摄影机(眼睛)连一条线穿过这个像素,然后打出去一根光线,在场景中如果与物体相交,就说明我沿着这个方向看看到了这个点,再把这个点和光源连线,判定这个点是不是对光源也可见(不可见即为在阴影里)。如果这个点对光源也可见,则证明光路有效,那么就可以记录这条光路上的能量,算出来后着色。
Ray Casting - Generating Eye Rays
Pinhole Camera Mode
首先做几个假设:
①、眼睛是针孔摄像机,假设为一个点
②、光源假设是点光源
③、反射折射是完美的(镜面反射)
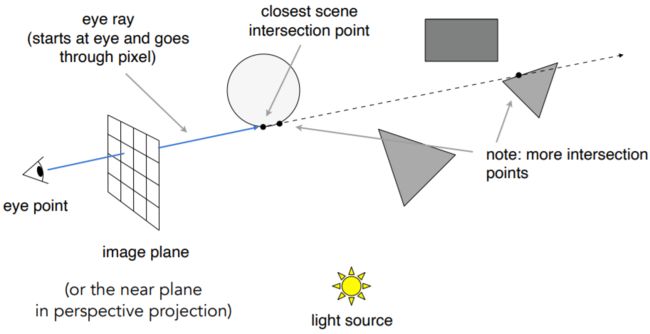
从眼睛到一个像素连出一条线(eye ray),碰到最近的物体上某点(closest scene intersection point)。到这里已经解决了光栅化中的深度缓存问题!

然后沿着这个点到光源做一条连线,如果在这条线上没有其他物体阻挡,则说明光源可以照亮这个点,如果有物体阻挡,则说明这个点在阴影中。然后就可以算这个点的着色,写入像素的值。
3、Recursive Ray Tracing(Whitted-Style Ray Tracing)

还是刚刚那个操作,打出的一条光线在碰到玻璃球球时会有反射光线,如上图所示,光线弹射后能量会有损失,继续向前走。

同时,在这个玻璃球内部还会有折射现象,折射光也会沿光路继续向前走,能量也有损失。
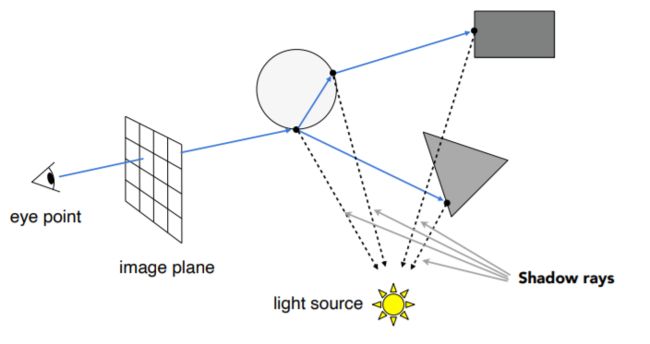
在每一个反射或折射的点都去和光源做一条连线,去判断可见性,如果有被物体挡住的线,则照亮不了,否则可以被照亮,进行着色。把所有着色的值都加到这个像素的值中去。

primary ray:第一次弹射前的连线(光线首次碰到的点与眼睛点间的连线)
secondary rays:第一次弹射后其他后面所有弹射的连线
shadow rays:判断可见性的连线(弹射点与光源间的连线)
(二)、Ray-Surface Intersection
1、Ray Equation
Ray is defined by its origin and a direction vector

Ray equation:
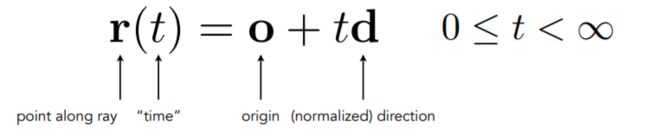
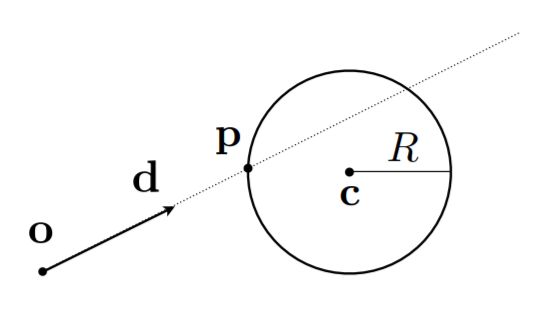
对于光线上任意一点r,在t时间,都可以表示为从起始位置o,加上t乘以方向d。对于t来讲,由于这里是射线,而且t表示时间,所以t的取值不能取负。
2、Ray Intersection With Implicit Surface
Ray Intersection With Sphere
光线的定义上面已经提到,对于球的定义,把隐函数的表示写出来(如上所示),球上任何一个点p到球心点c的距离都等于半径R
What is an intersection?
The intersection p must satisfy both ray equation and sphere equation
如果要求光线和球的交点,那么说明这个点既要满足光线上一点的定义也要满足球上一点的定义。那么联立上面两个式子,即可得到如下结果。
Solve for intersection:
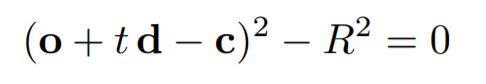
然后去解这个方程,利用二次函数的求解方法即可得到t。
如果相交可以求出两个不同的t,取最近的,即取最小的t。
Ray Intersection With Implicit Surface
Ray:![]()
Substitute ray equation:![]()
Solve for real, positive roots

将刚刚的方法推广到所有一般隐式表面中,即有上式的方法。
3、Ray Intersection With Triangle Mesh
Why?
- Rendering: visibility, shadows, lighting …
- Geometry: inside/outside test
How to compute?
Let’s break this down:
- Simple idea: just intersect ray with each triangle
- Simple, but slow (acceleration?)
- Note: can have 0, 1 intersections (ignoring multiple intersections)
通过三角形和光线求交的问题,可以判断这个点是不是在三角形内部:
在2D中任意画一个封闭的曲线形状,在里面点一个点,从这个点向任意方向画一条线,与这个形状的交点总是为奇数个(只要点在封闭形状内部)
Triangle is in a plane
- Ray-plane intersection
- Test if hit point is inside triangle

如何判定光线和三角形相交?
由于三角形在平面内,因此这个判定过程就被分解成了两部分
①、光线和平面相交
②、找到交点以后在判断交点是不是在三角形内
Plane Equation
Plane is defined by normal vector and a point on plane

Plane Equation (if p satisfies it, then p is on the plane):

定义平面:一个方向N和一个点p‘(点法式)。
Ray Intersection With Plane
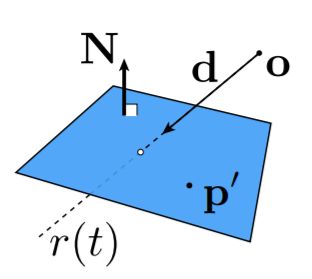
一个点若要既在光线上又在平面上,那么应该同时满足这两个式子。联立这两个式子,得出如下结果。
Solve for intersection:

那么有没有办法一次解出光线和三角形的交点?解出来之后立刻就能判定交点是否在三角形内?
Möller Trumbore Algorithm
A faster approach, giving barycentric coordinate directly
Derivation in the discussion section!
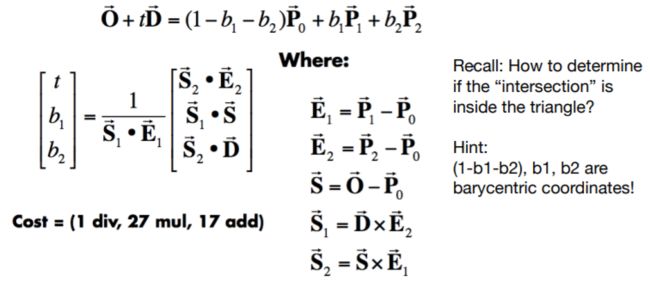
这个算法可以解决上述问题。
如果一个点在三角形内就可以写成用重心坐标描述的位置。而O+tD描述的是光线上的一个点,两者相等的话,就可以得到结果。
用克莱姆法则可以解出这个式子(如上图所示)。
(三)、Accelerating Ray-Surface Intersection——Bounding Volumes
Ray Tracing – Performance Challenges
Simple ray-scene intersection
- Exhaustively test ray-intersection with every triangle
- Find the closest hit (i.e. minimum t)
Problem:
- Naive algorithm = #pixels ⨉ # traingles (⨉ #bounces)
- Very slow!
For generality, we use the term objects instead of triangles later (but doesn’t necessarily mean entire objects)
如果用上面提到的方法直接去暴力计算,计算量太大,因此绝对不可以。
Bounding Volumes
Quick way to avoid intersections: bound complex object with a simple volume
- Object is fully contained in the volume
- If it doesn’t hit the volume, it doesn’t hit the object
- So test BVol first, then test object if it hits

这里采用包围盒的方法,对于任意一个物体,用一个简单的形状将其包起来,确保这个物体一定在包围盒内。
如果一条光线连包围盒都碰不到,那么更不可能碰到包围盒中的物体。
Ray-Intersection With Box

Understanding: box is the intersection of 3 pairs of slabs
Specifically: We often use an Axis-Aligned Bounding Box (AABB) (轴对⻬包围盒)
i.e. any side of the BB is along either x, y, or z axis
在三维空间中,我们用一个长方体来做包围盒。我们将这个长方体理解为三个不同方向的对面形成的交集。(前后、上下、左右)
在实际操作中,我们一般采用AABB,即轴对齐包围盒。让形成的平面为xy、yz、xz平面,平行于坐标轴。
Ray Intersection with Axis-Aligned Box
2D example; 3D is the same! Compute intersections with slabs and take intersection of tmin/tmax intervals

先通过二维的来理解这个问题。
首先看光线与x平面的一个对面(两个面)之间的相交。即算出光线什么时候进入x0平面,什么时候离开x1平面,如上图左图所示,在tmin时刻进入x0平面(与x0平面相交),在tmax时刻离开x1平面(与x1平面相交)。
光线与y平面的判断同理(如上图中图)。
刚刚分别得到了x平面和y平面的进入、离开时刻,那么如何得到光线进入、离开整个盒子的时刻呢?
如上图右图,求线段交集。我们直接通过三维来解释这个问题。
Ray Intersection with Axis-Aligned Box
-
Recall: a box (3D) = three pairs of infinitely large slabs
-
Key ideas
--The ray enters the box only when it enters all pairs of slabs
--The ray exits the box as long as it exits any pair of slabs
-
For each pair, calculate the tmin and tmax (negative is fine)
-
For the 3D box, tenter = max{tmin}, texit = min{tmax}
-
If tenter < texit, we know the ray stays a while in the box (so they must intersect!) (not done yet, see the next slide)
如何判定光线进入这个盒子?又如何判定光线离开这个盒子?
光线进入所有对面(三个对面)的时候,才可以判定光线进入这个盒子,而当光线离开一个对面的时候,就可以判定光线离开这个盒子。
那么就可以得到一个算法,在三维空间中有三组对面,分别计算一次光线进入对面的最小时间和最大时间。由于光线进入所有对面(三个对面)的时候,才可以判定光线进入这个盒子,那么计算出光线进入三组对面各自的时间tmin的最大值,也就是光线最晚进入的那一组对面的时间,即为tenter,同理,由于光线离开一个对面的时候,就可以判定光线离开这个盒子,那么计算出光线离开三组对面各自的时间tmax的最小值,也就是光线最先离开的那一组对面的时间,即为texit。通过这个方式我们就可以明确得出光线什么时候(tenter)进入盒子,什么时候(texit)离开盒子。
如果进入时间tenter小于离开时间texit,说明这段时间光线就在盒子里。
下面我们要检查时间t的正负
-
However, ray is not a line
--Should check whether t is negative for physical correctness!
-
What if texit < 0?
--The box is “behind” the ray — no intersection!
-
What if texit >= 0 and tenter < 0?
--The ray’s origin is inside the box — have intersection!
-
In summary, ray and AABB intersect if f
--tenter < texit && texit >= 0
如果离开盒子的时间为负,则说明光线在盒子后面。无交点。
如果离开盒子的时间为正,而进入盒子的时间为负,则说明光线的起点就在这个盒子里面。一定有交点。
总结:当且仅当进入时间小于离开时间且离开时间非负,则证明有交点。
Why Axis-Aligned

为什么要用平行于坐标轴的对面?
光线与横平竖直的面求交好求!