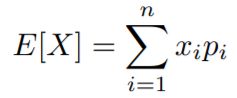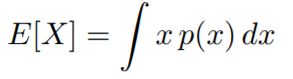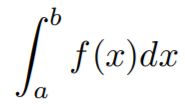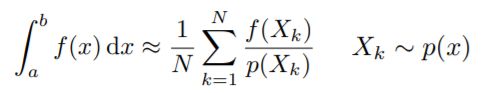GAMES101-现代计算机图形学入门-闫令琪——Lecture 16 Ray Tracing 4 学习笔记

Lecture 16 Ray Tracing 4

一、Probability Review

1、Random Variables

X：random variable. Represents a distribution of potential values

X~p(x)：probability density function (PDF). Describes relative probability of a random process choosing value

Example: uniform PDF: all values over a domain are equally likely

2、Expected Value of a Random Variable

n discrete values：x_i

with probability：p_i

Expected value of X:

3、Continuous Case: Probability Distribution Function (PDF)

概率密度函数

X~p(x)

A random variable X that can take any of a continuous set of values, where the relative probability of a particular value is given by a continuous probability density function p(x).

Conditions on p(x):

Expected value of X:

概率密度函数所有可能的取值（面积）为1

二、Monte Carlo Integration

Why: we want to solve an integral, but it can be too difficult to solve analytically.

当我们想求一个函数的积分值，但是由于函数太复杂，无法写出解析式，从而无法求出积分值的时候。我们通过蒙特卡洛积分来求。蒙特卡洛积分是一种数值方法，只考虑最后得到积分的值。

Let us define the Monte Carlo estimator for the definite integral of given function f(x)

Definite integral ：

Random variable：

通过一个例子来解释上述公式：

Example: Uniform Monte Carlo Estimator

Uniform random variable

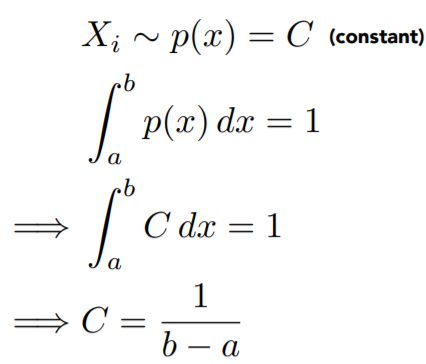
如果我想在a到b之间均匀采样，那么就说明采样中我们用的PDF应该是一个常数写作C。由于PDF在积分域上积分出来的结果是1，那么PDF解出来就是1/b-a。此处也可以这样理解：PDF在a到b上积分是1，又是个常数，所以图像应该是个矩形，我们知道这个矩形的底是b-a，面积又得是1，那么高就是1/b-a。

那么用蒙特卡洛积分的方法去算：

这也就是蒙特卡洛积分的一种特殊情况，即PDF是均匀的，式子如上图所示。

三、Path Tracing

1、Whitted-Style Ray Tracing: Problem

Whitted-style ray tracing:

• Always perform specular reflections / refractions
• Stop bouncing at diffuse surfaces

Whitted-style ray tracing对于光线的弹射方法：

①、当光线打到光滑物体上，会沿着镜面方向反射或沿折射方向折射

②、当光线打到漫反射物体，那么这条光线就停下来了

Are these simplifications reasonable?

High level: let’s progressively improve upon Whitted-Style Ray Tracing and lead to our path tracing algorithm!

但是这种方式是不对的，因此我们提出更高级的方式来解决这些问题。

Whitted-Style Ray Tracing: Problem 1

Where should the ray be reflected for glossy materials?

这两个茶壶，左边这个完全光滑，是镜面反射，右边这个相对来讲没有那么光滑。在Whitted-Style Ray Tracing下，对于镜面反射的物体来讲没有什么问题，但是对于表面有些粗糙的物体，反射的光线应该朝向各个方向，如果认为还是认为沿着镜面反射方向反射，是不对的，因此这里产生了问题。

Whitted-Style Ray Tracing

Whitted-Style Ray Tracing: Problem 2

No reflections between diffuse materials?

上面这个场景是用路径追踪得到的，场景中的物体都是漫反射的，而如果用Whitted-style ray tracing，其定义当光线打到漫反射物体，那么这条光线就停下来了，那么两个物体之间的光线全部都得不到。

因此

Whitted-Style Ray Tracing is Wrong

But the rendering equation is correct

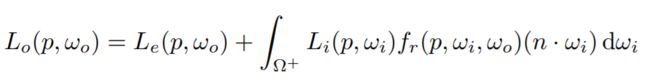
But it involves

• Solving an integral over the hemisphere, and
• Recursive execution

How do you solve an integral numerically?

虽然Whitted-Style Ray Tracing是错的，但是渲染方程是对的。为了解这个渲染方程，考虑

①、光是来自四面八方的，要考虑对半球积分

②、接收到的光照来源于光源还是物体反射不做区分，所以要做递归

下面就来解决这些问题。

2、A Simple Monte Carlo Solution（Direct illumination）

Suppose we want to render one pixel (point) in the following scene for direct illumination only

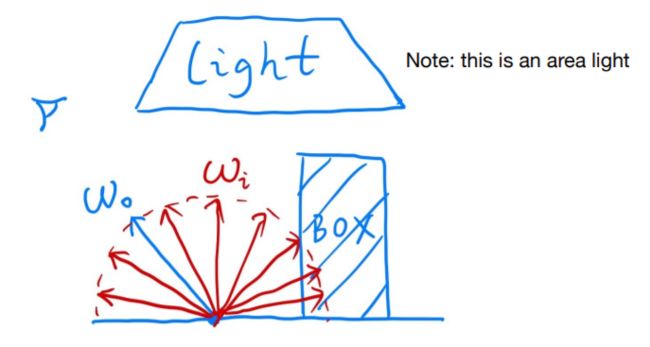
在这一个简单场景中，我们就考虑清楚对于一个点（像素），他的直接光照是什么。

①、有可能有其他物体会挡住光

②、有一个相对较大的面光源

③、观测方向：着色点到摄像机的方向ω_o

④、各个不同的进来的光（入射光方向）：ω_i（与Blinn-Phong一样，认为方向都是从着色点出发往外打）

Abuse the concept of Reflection Equation a little bit

Fancy as it is, it’s still just an integration over directions

So, of course we can solve it using Monte Carlo integration!

我们只考虑直接光照，不考虑其他物体反射过来的光，因此这里L_i就是光源的。

这个式子就是在半球上的一个积分，那么在这里我们就可以用蒙特卡洛积分去解这个式子。

We want to compute the radiance at p towards the camera

Monte Carlo integration:

What’s our “f(x)”?

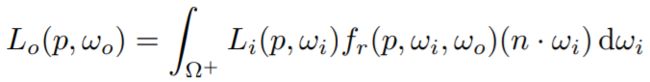
What’s our pdf?

（assume uniformly sampling the hemisphere）

在这里我们假设对半球进行均匀的采样，那么蒙特卡洛积分式子的各个部分我们都已经知道（如上所示）

So, in general

What does it mean?

A correct shading algorithm for direct illumination!

对照着上面的式子，可以把着色算法写出来：

shade(p, wo)//对于任意一点p，考虑沿着ωo方向出来算Lo
	Randomly choose N directions wi~pdf//在半球上选N个方向采样
	Lo = 0.0//先将最后的结果初始化
	For each wi//对于任意一个选中的方向
		Trace a ray r(p, wi)//考虑从p点向那个方向ωi连出一条光线
		If ray r hit the light//如果这根光线打到了光源
			Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)//那么就把这个式子写出来（光线打到了光源自然就知道了各个值）
	Return Lo

到这里基本的直接光照部分已经结束了

3、Introducing Global Illumination

刚刚解决的只是直接光照的问题，但是我们最后的结果要是全局光照，因此再引入间接光照。

One more step forward: what if a ray hits an object?

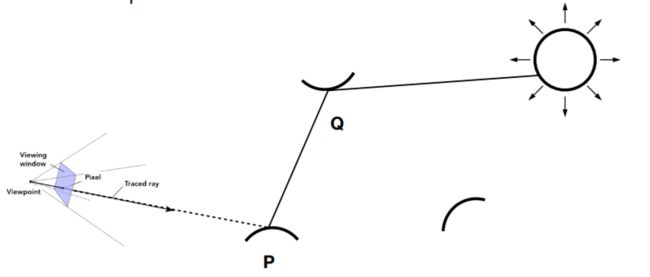
在这里我们要考虑光从Q点反射到P点，该怎么办？

Q also reflects light to P! How much? The dir. illum. at Q!

由于渲染方程中不区分光源的Radiance和物体反射的光的Radiance，所以我们同样也可以把Q点看成光源，Q点反射到P点的Radiance就是Q点光源发出的Radiance。这个时候我们类比，就好像是在P点观察Q点，算出Q点的直接光照。Q点反射到P点的Radiance就相当于是在Q点算出的直接光照。

那么就可以对刚刚的算法做一些修改：

shade(p, wo)
	Randomly choose N directions wi~pdf
	Lo = 0.0
	For each wi
		Trace a ray r(p, wi)
		If ray r hit the light
			Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
		Else If ray r hit an object at q//如果打到的是物体（不是光源）
		Lo += (1 / N) * shade(q, -wi) * f_r * cosine/ pdf(wi)//考虑在q点以-ωi方向进来的光写出方程，这里相当于把Q点直接光照的结果作为P点过来的光照
	Return Lo

Is it done? No！

问题还没有结束！

4、Problem 1: Explosion of #rays as #bounces go up:

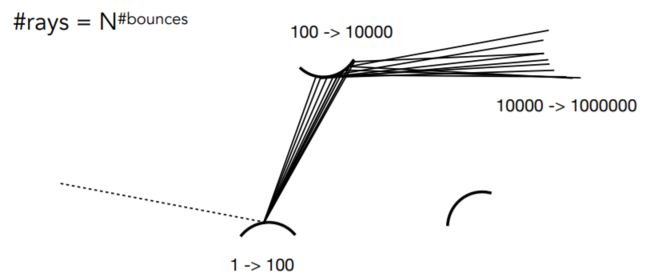
如果以这样的方式打出光线，光线的数量会爆炸。

往四面八方打出了N根光线，碰到物体后每条光线又会打出N根光线，碰到物体后每条光线又会打出N根光线…

Key observation: #rays will not explode iff N = ???

所以N取多少才能保证不出问题？

答案只能是N=1。

From now on, we always assume that only 1 ray is traced at each shading point:

shade(p, wo)
	Randomly choose ONE direction wi~pdf(w)//随机往一个方向采样ωi
	Trace a ray r(p, wi)//往一个方向打出一条光线
	If ray r hit the light
		Return L_i * f_r * cosine / pdf(wi)
	Else If ray r hit an object at q
		Return shade(q, -wi) * f_r * cosine / pdf(wi)

This is path tracing! (FYI, Distributed Ray Tracing if N != 1)

到此为止，用N=1来做蒙特卡洛积分，这就叫路径追踪。

But this will be noisy!

No problem, just trace more paths through each pixel and average their radiance!

用这种方法的噪声会非常大，但是由于最后要的是一个像素最后的值是多少，穿过一个像素的路径会有很多条，这些所有的路径取平均即可。也就是说用足够多的路径（path）即可解决问题。（之所以叫path，是因为每次打到一个点上只会往一个方向去反射，不是一次产生一束，这就形成了一条连接视点和光源的路径。）

Very similar to ray casting in ray tracing

这个过程的操作步骤与光线追踪中的光线投射非常类似：

ray_generation(camPos, pixel)//定义摄像机位置、要打出很多光线的像素
	Uniformly choose N sample positions within the pixel//在这个像素内均匀取N个位置
	pixel_radiance = 0.0
	For each sample in the pixel//对于任何一个选取的位置
		Shoot a ray r(camPos, cam_to_sample)//从视点（摄像机）位置向样本位置连一条光线
		If ray r hit the scene at p//如果光线打到了场景中某个位置
			pixel_radiance += 1 / N * shade(p, sample_to_cam)//计算该点的着色
	Return pixel_radiance

Now are we good? Any other problems in shade()?

shade(p, wo)
	Randomly choose ONE direction wi~pdf(w)
	Trace a ray r(p, wi)
	If ray r hit the light
		Return L_i * f_r * cosine / pdf(wi)
	Else If ray r hit an object at q
		Return shade(q, -wi) * f_r * cosine / pdf(wi)

这个算法到现在为止对了吗？并没有。这个算法是递归的，但是永远停不下来。

5、Problem 2: The recursive algorithm will never stop!

Dilemma: the light does not stop bouncing indeed!

Cutting #bounces == cutting energy!

3 bounces：

17 bounces：

如果直接规定反弹多少次就停止，这样一种从中间直接砍下来的结果会导致能量损失，但是又无法模拟与真实的自然界一样的无限次反弹。因此人们引入了一种方法：

Solution: Russian Roulette (RR)（俄罗斯轮盘赌）

Russian Roulette is all about probability

With probability 0 < P < 1, you are fine

With probability 1 - P, otherwise

Example: two bullets, Survival probability P = 4 / 6

举例：一把左轮手枪可以装6发子弹，如果里面装了2枚子弹，那么生存的概率就是4/6

通过用俄罗斯轮盘赌的方法，来决定一定的概率来停止继续往下进行追踪

Previously, we always shoot a ray at a shading point and get the shading result Lo

某一个着色点最后的结果Radiance算出来的是Lo，我们希望中间可以停掉，但是算出来的结果不能出错，还是Lo

Suppose we manually set a probability P (0 < P < 1)

自己定一个概率P

With probability P, shoot a ray and return the shading result divided by P: Lo / P

以一定的概率P打出一条光线，最后得出的结果Lo再去除以概率P

With probability 1-P, don’t shoot a ray and you’ll get 0

那么另外的1-P的概率就不打出光线

In this way, you can still expect to get Lo!: E = P * (Lo / P) + (1 - P) * 0 = Lo

这里仍然可以期望最后得到的结果是Lo。

将其以代码的形式表示出来:

shade(p, wo)
	Manually specify a probability P_RR//定义一个概率P_RR
	Randomly select ksi in a uniform dist. in [0, 1]//在计算机中随机取一个0到1的数ksi
	If (ksi > P_RR) return 0.0;//如果 ksi大于概率P_RR，意味着这根光线不能生存

	Randomly choose ONE direction wi~pdf(w)
	Trace a ray r(p, wi)
	If ray r hit the light
		Return L_i * f_r * cosine / pdf(wi) / P_RR//那么正常打光线的时候就去除以生存的概率P_RR即可
	Else If ray r hit an object at q
		Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

到此为止，这已经是一个正确的路径追踪的方法了。但是还有一些问题，这并不是多么高效。

6、Sampling the Light

按照上述的方法，如果打出的光线少，渲染速度快，但是得到的质量会有很多噪声，如果打出光线多，得到结果好但是速度慢。我们希望Low SPP情况下质量依然能够很好。

Understanding the reason of being inefficient

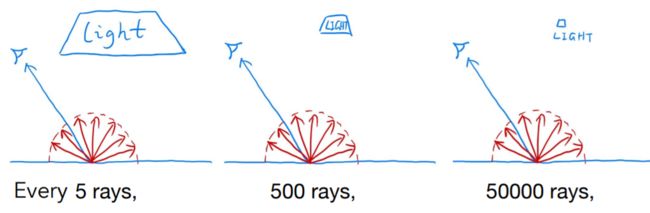
there will be 1 ray hitting the light. So a lot of rays are “wasted” if we uniformly sample the hemisphere at the shading point.

对于面积较大的面光源，可能我在着色点打出很少的光线就能碰到光源，但是如果面光源很小，那么我可能需要很多根光线才能有一根打到光源，这个就完全是看运气，就会造成很多光线浪费。

如果我们直接从光源上采样，那么所有光线都不会被浪费了

Monte Carlo methods allows any sampling methods, so we can sample the light (therefore no rays are “wasted”)

Assume uniformly sampling on the light: pdf = 1 / A (because ∫pdf dA = 1)

假设对于着色点在光源上采样，那么对于这个面光源来讲，光源面积是A，均匀采样的PDF就是1/A，

But the rendering equation integrates on the solid angle: Lo = ∫Li fr cos dω

但是渲染方程是定义在半球中立体角上的，而不是在光源上的，

Recall Monte Carlo Integration: Sample on x & integrate on x

Since we sample on the light, can we integrate on the light?

采样在光源上采样，积分在立体角上积分，如果要确保渲染方程还能用，就要把渲染方程写成在光源上的积分。

Need to make the rendering equation as an integral of dA

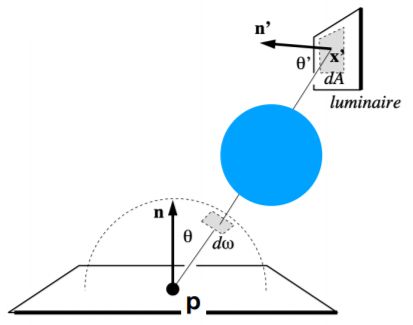
Need the relationship between dω and dA

我们只需要知道dω和dA的关系即可。

dA是光源上一个小的表面，dω是单位球上的立体角

Recall the alternative def. of solid angle: Projected area on the unit sphere

我们之前说过立体角是半球上的面积除以半径的平方，也可以理解为把任何一个面积投影到单位球的表面上所对应的面积除以1单位长度的平方

那么把dA往单位球上作投影，即可算出：

​ (Note: θ’, not θ)

Then we can rewrite the rendering equation as

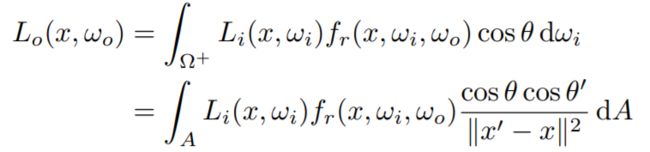
这样我们就可以把渲染方程成上述式子。

Now an integration on the light!

Monte Carlo integration: “f(x)”: everything inside

Pdf: 1 / A

这时式子就变成了对光源进行采样，对光源进行积分。

Previously, we assume the light is “accidentally” shot by uniform hemisphere sampling

之前我们是盲目的采样，打到打不到光源要看运气

Now we consider the radiance coming from two parts:

①、light source (direct, no need to have RR)

②、other reflectors (indirect, RR)

现在我们可以直接对光源采样。这样就可以把算法重写。

这时我们把着色结果分为两部分：

第一部分来源于对光源的贡献，对光源采样

第二部分来源于其他所有非光源的贡献（如物体反射的光），这部分还用原来的方法做

shade(p, wo)
	# Contribution from the light source.//光源对这一点的贡献
	Uniformly sample the light at x’ (pdf_light = 1 / A)//均匀地对光源进行采样
	L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light//在光源上积分
    
	# Contribution from other reflectors.//其他所有非光源的贡献
	L_indir = 0.0
	Test Russian Roulette with probability P_RR//用俄罗斯轮盘赌测试
	Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)//如果通过了俄罗斯轮盘赌的测试，则发出一条光线
	Trace a ray r(p, wi)//间接光照，从物体p向ωi方向打出一条光线
	If ray r hit a non-emitting object at q//打到了点q，确定点q不是光源（因为光源的贡献已经算出来了）
		L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR
    
	Return L_dir + L_indir//两部分加起来

One final thing: how do we know if the sample on the light is not blocked or not?

如果光源和着色点之间被其他物体挡到，则不能算进去这个着色点在光源处的采样，我们在p点和光源取一条连线，判断中间有没有碰到其他物体即可。

# Contribution from the light source.
L_dir = 0.0
Uniformly sample the light at x’ (pdf_light = 1 / A)
Shoot a ray from p to x’
If the ray is not blocked in the middle
	L_dir = …

Now path tracing is finally done!

到此为止，路径追踪全部结束！

（四）、Some Side Notes

Is Path Tracing Correct?

Yes, almost 100% correct, a.k.a. PHOTO-REALISTIC

The Cornell box — http://www.graphics.cornell.edu/online/box/compare.html

Ray tracing: Previous vs. Modern Concepts

• Previous

  ​ — Ray tracing == Whitted-style ray tracing

• Modern (my own definition)

  ​ --The general solution of light transport, including

  ​ -- (Unidirectional & bidirectional) path tracing

  ​ --Photon mapping

  ​ --Metropolis light transport

  ​ --VCM / UPBP…

Things we haven’t covered / won’t cover

• Uniformly sampling the hemisphere

  ​ --How? And in general, how to sample any function? (sampling)

• Monte Carlo integration allows arbitrary pdfs

  ​ --What’s the best choice? (importance sampling)

• Do random numbers matter?

  ​ --Yes! (low discrepancy sequences)

• I can sample the hemisphere and the light

  ​ --Can I combine them? Yes! (multiple imp. sampling)

• The radiance of a pixel is the average of radiance on all paths passing through it

  ​ --Why? (pixel reconstruction filter)

• Is the radiance of a pixel the color of a pixel?

  ​ --No. (gamma correction, curves, color space)

• Asking again, is path tracing still “Introductory”?

  ​ --This time, yes. Fear the science, my friends.

可以看到，虽然路径追踪的大体思路讲完了，但是依然还有很多细节上的问题根本没有提到。整个路径追踪的内容太多了。现在的研究依然在向这个方向努力。