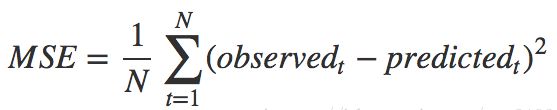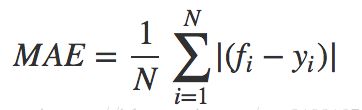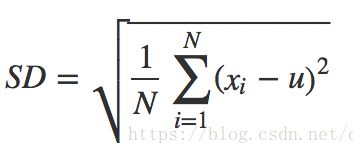深度学习常用评价指标
版权声明:本文为CSDN博主「ZONG_XP」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/zong596568821xp/article/details/80797695
一、根据深度学习的任务不同,评价标准也不同,分类任务和回归任务的评价指标如下:
- 分类:accuracy、误分类率、precision、recall、F1 score、ROC 曲线、AUC、PR曲线、AP、mAP等
- 回归:MAE、MSE
二、符号定义
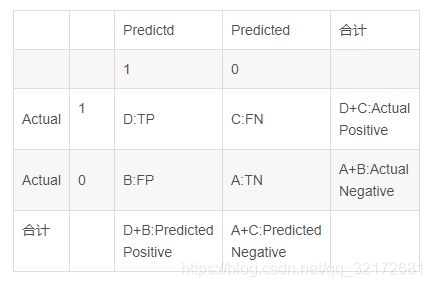
根据分类时预测与实际的情况,作出如下表格,称为混淆矩阵,其中1代表正类,0代表负类,Predicted代表预测,Actual代表实际
- A: TN=True Negative 真负,将负类预测为负类的数量
- B: FP=False Positive 假正,将负类预测为正类的数量,可以称为误报率
- C: FN=False Negative 假负,将正类预测为负类的数量,可以称为漏报率
- D: TP=True Positve 真正,将正类预测为正类的数量
- A+B: Actual Negative 实际上负类的数量
- C+D: Actual Positive 预测的负类数量
- A+C: Predicted Negative 预测的负类数量
- B+D: Predicted Positive 预测的正类数量
三、深度学习常用评价指标
1、accuracy
准确率=正确预测的正反例数/总数
ACC=(TP+TN)/(TP+TN+FP+FN)=(A+D)/(A+B+C+D)
2、precision
精确率是指分类正确的正样本占预测为正的正样本的比例
精确率是针对预测结果而言的,表示的是预测为正的样本中有多少是真正的正样本,预测为正就有两种可能,一种是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),即 P = TP / (TP+FP)
查准率、精确率=正确预测到的正例数/预测正例总数
precision=TP/(TP+FP)=D/(B+D)
3、recall
精确率是指分类正确的正样本占真正的正样本的比例
召回率是针对原来样本而言的,表示的是样本中的正例有多少被预测正确,同样也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN),即 R = TP / (TP+FN)
查全率、召回率=正确预测到的正例数/实际正例总数
recall=TP/(TP+FN)=D/(C+D)
4、ROC curve
逻辑回归里面,对于正负例的界定,通常会设一个阈值,大于阈值的为正类,小于阈值为负类。如果我们减小这个阀值,更多的样本会被识别为正类。提高正类的识别率,但同时也会使得更多的负类被错误识别为正类。为了直观表示这一现象,此处引入ROC,ROC曲线可以用于评价一个分类器好坏。
ROC曲线的优点是不会随着类别分布的改变而改变,但这在某种程度上也是其缺点。因为负例N增加了很多,而曲线却没变,这等于产生了大量FP。像信息检索中如果主要关心正例的预测准确性的话,这就不可接受了。在类别不平衡的背景下,负例的数目众多致使FPR的增长不明显,导致ROC曲线呈现一个过分乐观的效果估计。
ROC关注两个指标:
True Positive Rate: TPR = TP / (TP+FN) → 将正例分对的概率
Fales Positive Rate: FPR = FP / (FP+TN) → 将负例错分为正例的概率
在 ROC 空间中,每个点的横坐标是 FPR,纵坐标是 TPR,这也就描绘了分类器在 TP(真正率)和 FP(假正率)间的 trade-off。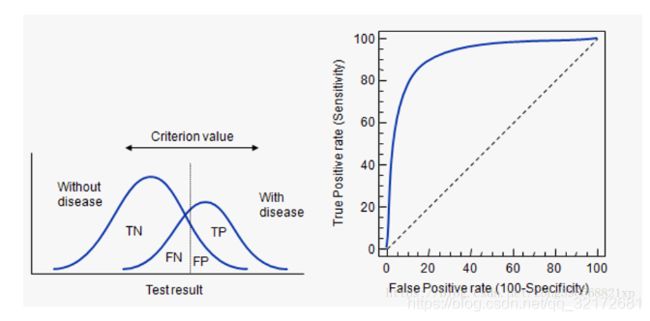
ROC曲线中的四个点和一条线:
点(0,1):即FPR=0, TPR=1,意味着FN=0且FP=0,将所有的样本都正确分类;
点(1,0):即FPR=1,TPR=0,最差分类器,避开了所有正确答案;
点(0,0):即FPR=TPR=0,FP=TP=0,分类器预测所有的样本都为负样本(negative);
点(1,1):分类器实际上预测所有的样本都为正样本。
总之:ROC曲线越接近左上角,该分类器的性能越好。
5、AUC
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。随机挑选一个正样本以及一个负样本,分类器判定正样本的值高于负样本的概率就是 AUC 值。总之:AUC值越大的分类器,正确率越高。
AUC = 1:绝对完美分类器,理想状态下,100%完美识别正负类,不管阈值怎么设定都能得出完美预测,绝大多数预测不存在完美分类器;
0.5
AUC<0.5:比随机猜测还差;但只要总是反预测而行,就优于随机猜测,因此不存在AUC<0.5的状况。
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反)
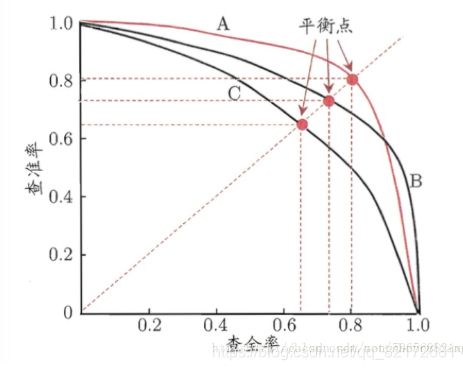
6、PR曲线
PR曲线即查准率(Precision)与查全率(Recall),以查全率为坐标x轴,查准率为坐标y轴,从而画出了一条曲线。
P-R图直观地显示出学习器在样本总体上的查全率和查准率。在进行比较时,若一个学习器的P-R曲线完全被另一个学习器的曲线完全“包住”,则我们就可以断言后者的性能优于前者。
PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例,所以在此情况下PR曲线被广泛认为优于ROC曲线。
若想评估一个分类器的性能,一个比较好的方法就是:观察当阈值变化时,Precision与Recall值的变化情况。如果一个分类器的性能比较好,那么它应该有如下的表现:在Recall值增长的同时,Precision的值保持在一个很高的水平。而性能比较差的分类器可能会损失很多Precision值才能换来Recall值的提高。通常情况下,文章中都会使用Precision-recall曲线,来显示出分类器在Precision与Recall之间的权衡。
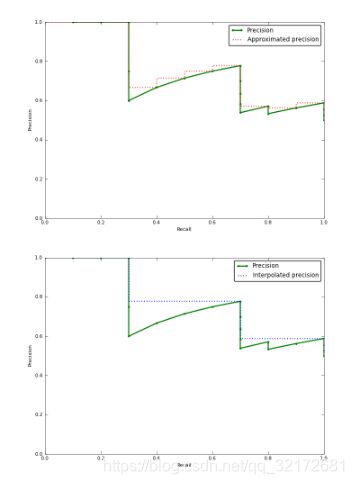
7、AP与mAP
严格的AP就是PR曲线下的面积,mAP就是所有类AP的算术平均
但是一般都是用逼近的方法去估计这个面积,比如
approximated precision的方法:每个recall point都approximate,计算每个矩形面积求和(下图红色虚线)
Interpolated Precision的方法:从每个recall point往后看,用最大的precision作为插值来,计算每个矩形面积求和(下图蓝色虚线)
从PASCAL VOC 2007开始,就是用的类似Interpolated Precision的方法,不过稍有不同的是,VOC使用的是在固定的11个recall([.0,.1,.2,.3,.4,.5,.6,.7,.8,.9,1.])的地方取precision然后来近似AP,所以又叫11-point interpolated average precision。
而从PASCAL VOC 2010开始,又摈弃了11-point interpolated average precision的计算方法,取而代之的是用所有的(recall, precision)数据点(只要是recall有改变的地方)来计算AP。具体而言就是,取所有recall改变的数据点及其后的最大的precision作为当前recall的precion(这样就能得到一条单调递减的(recall, precision)曲线)来计算矩形面积,然后累加所有小矩形,即得AP。
用上述方法分别算出各个类的AP,然后取平均,就得到mAP了。AP的计算可以直接统计该类别下的TP,FP和postitive number的总数,然后就可以一次性算出AP了。得到了各类的AP,mAP就是各类别AP的算术平均!mAP的好处是可以防止AP bias到某一个数量较多的类别上去。
8、均方误差(MSE)
MSE: Mean Squared Error
均方误差是指参数估计值与参数真值之差平方的期望值;
MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
9、均方根误差(RMSE )
均方误差:均方根误差是均方误差的算术平方根
10、平均绝对误差(MAE)
MAE :Mean Absolute Error
平均绝对误差是绝对误差的平均值
平均绝对误差能更好地反映预测值误差的实际情况.
11、标准差(SD)
SD :standard Deviation
标准差:标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组组数据,标准差未必相同。
u表示平均值
ROC、PR参考:https://www.imooc.com/article/48072