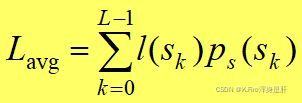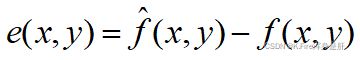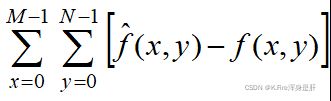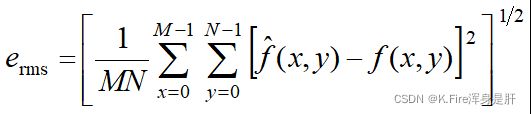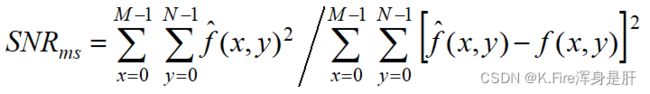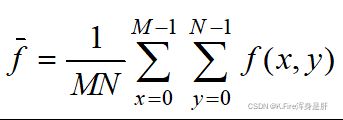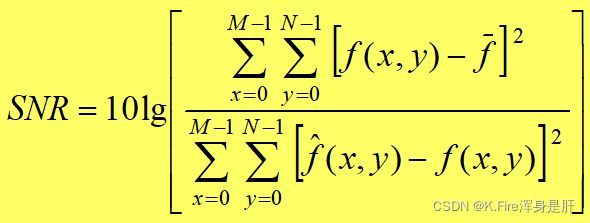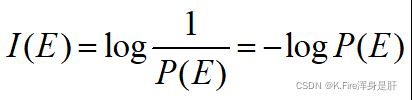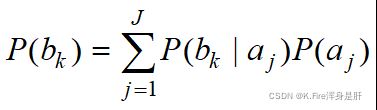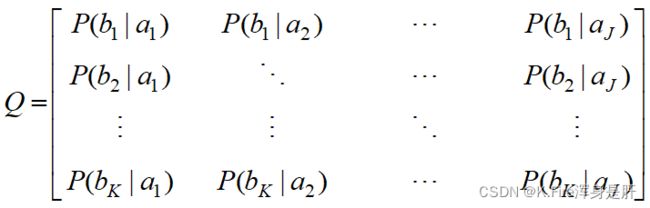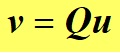【基于MATLAB的数字图像处理】第五章·图像编码
系列文章
·【基于MATLAB的数字图像处理】第一章·绪论
·【基于MATLAB的数字图像处理】第二章·视觉系统与图像处理系统
·【基于MATLAB的数字图像处理】第三章·基本图像变换
·【基于MATLAB的数字图像处理】第四章·图像增强
·【基于MATLAB的数字图像处理】第五章·图像编码
·【基于MATLAB的数字图像处理】第六章·形态学图像处理
·【基于MATLAB的数字图像处理】大作业·综合图像处理平台
目录
一、基础知识
1.数据冗余
a.编码冗余
b.像素相关冗余
c.心理视觉冗余
2.保真度准则
a.客观保真度准则
b.主观保真度准则
3.图像编码模型
4.信息论的基础理论
二、无损压缩编码
1.霍夫曼编码
2.香农-法诺编码
3.算术编码
三、限失真编码
1.信息率失真定理
2.预测编码
a.无损预测编码
b.有损预测编码
3.正交变换编码
例程
首先阐明图像编码的动机:表达数字图像所需数据量通常很大,比如在MATLAB中图像使用矩阵存储,每个像素点都还有三个通道,占用的内存空间巨大,特别是在进行实时传输时,对传输数据的要求很高,必须小于通讯带宽,因此提出通过对图像进行重新编码,以减小所需的数据量。
图像压缩方式分为:信息保存型(无损压缩)和信息损失型(有损压缩)
- 无损压缩:在压缩和解压过程中没有信息损失
- 有损压缩:解压后图像不能恢复原状
一、基础知识
1.数据冗余
数据冗余是指数据表达了无用的信息或表达了已表达的信息,比如平时交流中的“废话”、还比如RGB三色表示法中,很多肉眼分辨不出来的颜色,这时我们就可以进行图像压缩,压缩掉图像中的视觉冗余。
数据冗余可定量描述,相对冗余:![]()
![]() 称为压缩率,n1和n2代表2个数据集合中的信息载体单位的个数
称为压缩率,n1和n2代表2个数据集合中的信息载体单位的个数
数据冗余包括三种冗余:编码冗余、像素相关荣誉、心理视觉冗余,减少其中的一种冗余,即可达到数据压缩的效果。
a.编码冗余
编码:需建立码本来表达数据
码本:用来表达一定量信息或一组事件所需的一系列符号(如字母、数字等)
码字:对每个信息或事件所赋的码符号序列(如:0101011)
如果一个图像的灰度级编码,使用了多于实际需要的编码符号,就称该图像包含了编码冗余,例如用8bit量化去表示一个二值图像。
每个灰度值出现的概率:
每个数值的位数为l(sk)那么平均位数为:
根据这个式子可以得出:用较少的比特数表示出现概率较大的灰度级,用较多的比特数表示出现概率较小的灰度级就可以达到压缩图像的效果。
变长最佳编码定理:如果码字长度严格按照所对应的符号出现概率的大小逆序排列,则编码结果的平均码字长度一定小于任何其他排列形式。
b.像素相关冗余
由于任何给定的像素值,原理上都可以通过它的相邻像素预测到,单个像素携带的信息相对是小的,对于一个图像,很多单个像素对视觉的贡献是冗余的。这是建立在对邻居值预测的基础上。再比如说有些图像中物体表面的大片灰度值都相同,这就产生了像素冗余;例:原图像数据:234 223 231 238 235 压缩后数据:234 -11 8 7 -3 ,可对一些接近于零的像素不进行存储,从而减小了数据量。
为减少像素间冗余,需将常用的2D像素矩阵表达形式转换为某种更有效的表达形式,这种减少像素间冗余的转换称为映射。
c.心理视觉冗余
心理视觉冗余的存在与人观察图像的方式有关,眼睛对某些视觉信息更敏感、人对某些视觉信息更关心,这就产生了心理视觉冗余,心理视觉冗余与实在的视觉信息有联系,损失不可逆转。
2.保真度准则
图像的保真度:描述解码图像相对于原始图像的偏离程度,分为主观保真度准则和客观保真度准则。
a.客观保真度准则
客观保真度准则是损失信息量用函数进行表示,最常用的准则是方均根误差
点误差:
图误差:
均方根误差:
另一个衡量保真度的准则是均方信噪比:
归一化信噪比(单位为分贝dB):
令:
则:
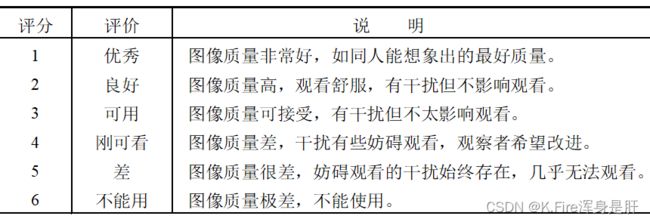
b.主观保真度准则
主观保真度准则是利用观察者对图像的评价综合平均起来得到一个统计的质量评估结果。
3.图像编码模型
两个通过信道级连的结构模块:
编码器中的信源编码器用来去除冗余信息进行数据压缩,信道编码器通过增加一些校验或容错用来增强传输过程中的抗噪声能力。
将编码器进行更进一步的拆解后,大致可分为三个模块:映射器、量化器、符号编码器
- 映射器:转换输入数据,减少像素间冗余,可反转
- 量化器:减少心理视觉冗余,量化(一种由多到少的映射),不可反转仅用于有损压缩
- 符号编码器:产生码本,通常采用变长码,可反转。
这三个部分不是必须的,比如如果要求无损压缩,则不能使用量化器。
4.信息论的基础理论
信息论是研究解码器的理论基础,给出了图像压缩的最终极限(熵)和图像传输率的最终极限(信道容量),下面介绍一些基本定义和概念。
概率为P(E)的随机事件 E 的信息量:
信息系统:信源通过信道与信宿(即信息用户)连通以传递自信息
信源符号集:A = {a1, a2, …, aJ};概率矢量:u = [P(a1) P(a2) … P(aJ )]T,使用这两个两就可以完全描述信源
信源平均信息(熵):
最大离散熵定理:在符号个数不变的情况下,信源中各符号的出现概率相等时,该信源的熵最大,这是进行的就是无损压缩,因此为保证无损压缩,平均码长需要大于熵,即熵是无损编码的下界。
信道信息:
因为信源的输出是一个离散随机变量,那么信道的输出和信宿的输入也是离散随机变量,可以也可以用下面的符号表示:
信道符号集:B = {b1, b2, …, bK}
概率矢量:v = [P(b1) P(b2) … P(bK)]T
用(B, v)可以完全描述信道输出和用户接受到的信息
写出信道输出概率P(bk )和信源u的概率分布:
写成矩阵形式:
那么输出符号集的概率分布可以表示为:
下面的我懒得写了,看不懂,我也不考,摆!
二、无损压缩编码
香农第一定理确定每个信源符号可以达到的最小平均码字长度。
无失真编码定理:在无干扰的条件下,存在一种无失真的编码方法,使编码的平均长度L与信源的熵H(s)任意地接近,即L=H(s)+ε,其中ε为任意小的正数,但以H(s)为其下限,即L≥H(s),
熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。
1.霍夫曼编码
霍夫曼编码是消除编码冗余最常用的技术,当对信源符号逐个编码时,霍夫曼编码能给出最短的码字,使出现频率高的字符用较短的码表示,使出现频率低的字符用较短的码表示。
Huffman编码过程:
- 首先求出图像中灰度分布的灰度直方图
- 根据该直方图,对其按照分布概率从小到大的顺序进行排列
- 每一次从中选择出两个概率为最小的节点相加,形成一个新的节点,构造一个称为“Huffman树”的二叉树
- 对这个二叉树进行编码,就获得了Huffman编码码字
2.香农-法诺编码
香农-法诺编码是一种变长编码技术,其码字中的0和1是独立的,并且基本上等概率出现。
其主要步骤为:
- 将信源符号依其概率从大到小排列
- 将尚未确定码字的信源符号分成概率和接近的两部分
- 分别给两部分的信源符号组合赋值
- 如果两部分均只有一个信源符号,编码结束,否则返回 (2)继续进行。
算法评价:
有时哈夫曼编码的结果与香农-法诺编码结果相同,在某些情况下,二者的编码结果也不同,且哈夫曼编码算法效率高一些。但两种编码都缺乏构造性,解码时需要通过查表来确定,对计算机的内存要求较大。
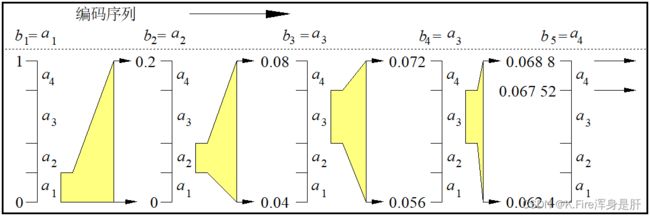
3.算术编码
算数编码是将要压缩的数据映射到[0,1)实数区间中的某一区段上的实数X,该实数的二进制展开式即为原符号串的压缩编码结果。
算术编码通过对当前的概率区间作迭代分割来确定实数。是具体构造出的用小数表示信息的方法。小数随位数的增加,它的精度也随之提高,从信息的角度来说,它所含有的信息量也随之增加。
三、限失真编码
以上所讨论的编码方法主要都是无损编码方法。在许多实际应用中,为取得高的压缩率,常使用一些有损的编码方法。与图像增强技术对应,在图像编码过程中也有对应空域技术的预测编码方法和对应频域技术变换编码方法。
1.信息率失真定理
在允许传输消息出现一定的失真条件下,传输该消息所需的信息率(最小值)将会比不允许失真时小,并且允许的失真度越大,则信息率(最小值)允许减小的程度就越大。
信息率失真函数:实际问题中,信号有一定的失真可以容忍。当失真大于某一限度后,信息质量将被严重损伤,丧失其实用价值。失真函数规定失真限度,一个定量的失真测度。
2.预测编码
预测编码是一种空域方法,用来消除像素间的冗余,基本思想是仅提取每个像素中的新信息并对它们编码(新信息:该像素当前值与预测值的差)
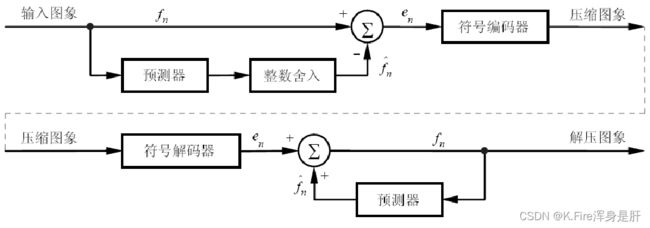
a.无损预测编码
无损预测编码系统:
无损预测编码过程
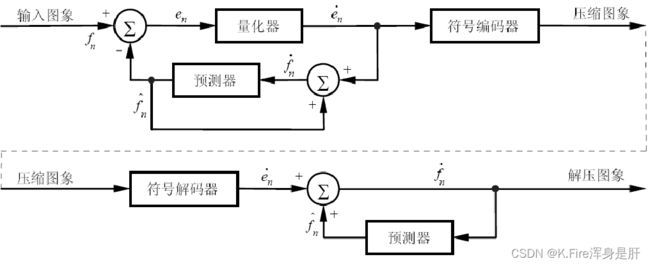
b.有损预测编码
有损预测编码系统:
有损预测编码过程:
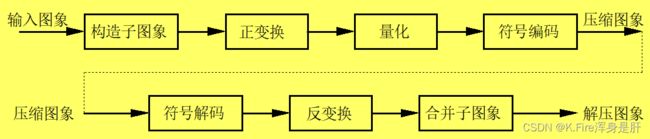
3.正交变换编码
正交变换编码是一种频域方法,不是信息保持型编码
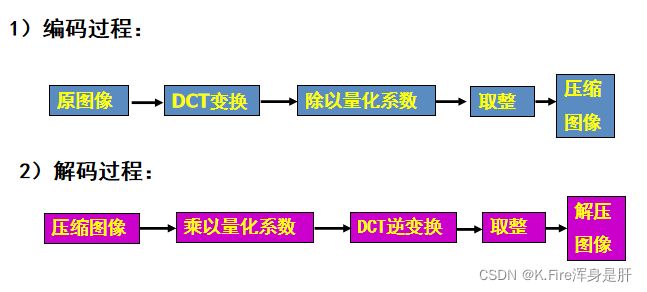
其中比较常用的是DCT编码,DCT变换是希望在接收方不产生误解的前提下进行一定的信息丢失,采用忽略视觉不敏感的部分进行有损压缩。
例程
function h = entropy(x,n)
%x:图像 %图像灰度级
%计算输入图像的熵
narginchk(1,2);
if nargin<2
n=256;
end
x=double(x);
xh=hist(x(:),n); %求图像直方图
xh=xh/sum(xh(:)); %求各灰度级出现的概率
i=find(xh);
h=-sum(xh(i).*log2(xh(i)));
end%%使用离散余弦变换进行图像压缩
clear all;
I=imread('Lena.tif');
I=im2double(I);
T=dctmtx(8); %图像存储类型转换
B=blkproc(I,[8 8],'P1 * x * P2',T,T'); %离散余弦变换
mask=[1 1 1 1 0 0 0 0;1 1 1 0 0 0 0 0;
1 1 0 0 0 0 0 0;1 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0];
B2=blkproc(B,[8 8],'P1 .* x',mask);
I2=blkproc(B2,[8 8],'P1 * x * P2',T',T);
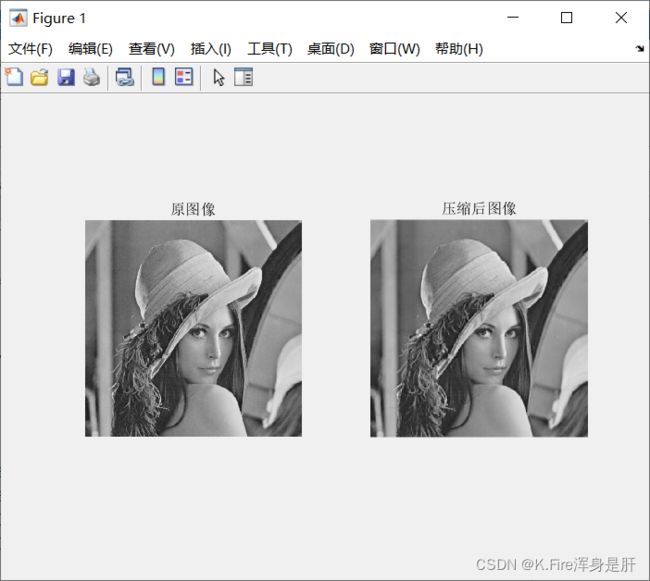
subplot(121);imshow(I);title('原图像');
subplot(122);imshow(I2);title('压缩后图像');