过拟合-权重正则化和Dropout正则化
文章目录
-
- 4.1、权重正则化
-
- 4.1.1、简介
- 4.1.2、从零开始实现
- 4.1.3、使用Pytorch的简洁实现
- 4.2 Dropout正则化
-
- 4.2.1、简介
- 4.2.2、从零开始实现
- 4.2.3、简洁实现
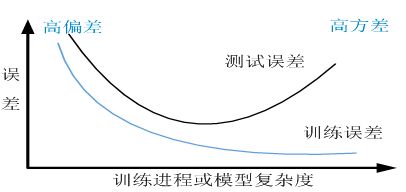
对模型进行评估和优化的过程往往是循环往复的。在训练模型的过程中,经常会出现刚开始训练时,训练和测试精度不高,这时的模型时 欠拟合,然后通过增加迭代次数或者通过优化,训练精度和测试精度继续提升。但随着训练迭代次数的增加或不断优化,有可能会出现训练精度和损失值继续改善,但测试精度或损失值不降反而上升的情况,如下图所示,这就是出现了 过拟合,这时的模型开始学习仅和训练数据有关的模式,但是这种模式对新数据来说是错误或无关紧要的。
为了防止模型从训练数据中学到错误或无关紧要的模式,最优的解决方法是获取更多的训练数据。模型训练的训练数据越多,泛化能力自然也越好。如果无法获取更多的数据,次优的解决方法是调节模型允许存储的信息量,或对模型允许存储的信息加以约束。如果一个网络只能记住几个模式,那么优化过程会迫使模型集中学习最重要的模式,这样更可能得到良好的泛化。这种降低过拟合的方法叫做正则化。
4.1、权重正则化
4.1.1、简介
给定一些训练数据和一种网络结构,很多组权重值(即很多模型)都可以解释这些数据。简单的模型比复杂模型更不容易过拟合。这些简单模型是指参数分布的熵更小的模型(或参数更少的模型)。因此一种常见的降低过拟合的方法就是强制让模型的权重只能取较小的值,从而限制模型的复杂度,这使得权重值的分布更规则。
这种方法叫作权重正则化,其实现方法是向网络损失函数中添加与较大权重值相关的成本。这个成本有两种形式:
- L1正则化(L1 regularization):添加的成本与权重系数的绝对值(权重的L1范数)成正比。
- L2正则化(L2 regularization):添加的成本与权重系数的平方(权重的L2范数)成正比。神经网络的L2正则化也叫权重衰减(weight decay)。
下面详细介绍和使用 L 2 L_2 L2范数正则化。 L 2 L_2 L2范数正则化在模型原损失函数基础上添加 L 2 L_2 L2范数惩罚项,从而得到训练所需要最小化的函数。 L 2 L_2 L2范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归损失函数为例:
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w T x ( i ) + b − y ( i ) ) 2 L(w, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(w^Tx^{(i)} + b - y^{(i)}\right)^2 L(w,b)=n1i=1∑n21(wTx(i)+b−y(i))2
其中 w w w是权重参数, b b b是偏差参数,样本 i i i的输入为 x ( i ) x^{(i)} x(i),标签为 y ( i ) y^{(i)} y(i),样本数为 n n n。带有 L 2 L_2 L2范数惩罚项的新损失函数为:
L ( w , b ) + λ 2 ∥ w ∥ 2 L(w, b) + \frac{\lambda}{2} \|\boldsymbol{w}\|^2 L(w,b)+2λ∥w∥2
其中超参数 λ > 0 \lambda > 0 λ>0。当权重参数均为0时,惩罚项最小。当 λ \lambda λ较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当 λ \lambda λ设为0时,惩罚项完全不起作用。有了 L 2 L_2 L2范数惩罚项后,在小批量随机梯度下降中,我们将线性回归一节中权重 w w w和的迭代方式更改为:
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( x ( i ) w T + b − y ( i ) ) , \begin{aligned} w &\leftarrow \left(1- {\eta\lambda} \right)w - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x^{(i)} \left(x^{(i)} w^T + b - y^{(i)}\right),\\ \end{aligned} w←(1−ηλ)w−∣B∣ηi∈B∑x(i)(x(i)wT+b−y(i)),
可见, L 2 L_2 L2范数正则化令权重 w w w和先自乘小于1的数,再减去不含惩罚项的梯度。因此, L 2 L_2 L2范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。实际场景中,我们有时也在惩罚项中添加偏差元素的平方和。
4.1.2、从零开始实现
下面,以高维线性回归为例引入一个过拟合问题,并使用权重衰减来应对过拟合,首先导入所使用的相关包。
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
生成数据,生成数据的公式为:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ y = 0.05 + \sum_{i = 1}^d 0.01x_i + \epsilon y=0.05+i=1∑d0.01xi+ϵ
选择标签是关于输入的线性函数。 标签同时被均值为0,标准差为0.01高斯噪声破坏。 为了使过拟合的效果更加明显,我们可以将问题的维数增加到 d=200 , 并使用一个只包含20个样本的小训练集。
#生成y=Xw+b+噪声
def synthetic_data(w,b,num_example):
X=torch.normal(0,1,(num_example,len(w)))
y=torch.matmul(X,w)+b
y+=torch.normal(0,0.01,y.shape)
return X,y.reshape((-1,1))
#构造一个Pytorch数据迭代器
def load_array(data_arrays,batch_size,is_train=True):
dataset=data.TensorDataset(*data_arrays)
return
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
#生成训练数据
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
#生成测试数据
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
下面我们将从头开始实现权重衰减,只需将 L 2 L_2 L2范数惩罚项添加到原始目标函数中。
首先,我们将定义一个函数来随机初始化模型参数。
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
定义 L 2 L_2 L2范数惩罚项。这里只乘法模型的权重参数。实现这一惩罚最方便的方法是对所有项求平方后并将它们求和。
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
下面的代码将模型拟合训练数据集,并在测试数据集上进行评估。
#定义模型、损失函数和优化方法
def linreg(X,w,b):
#线性回归模型
return torch.matmul(X,w)+b
def squared_loss(y_hat,y):
#均方损失
return (y_hat-y.reshape(y_hat.shape))**2/2
def sgd(params,lr,batch_size):
#小批量随机梯度下降
with torch.no_grad():
for param in params:
param-=lr*param.grad/batch_size
param.grad.zero_()
#开始训练,lambd为0是没有添加权重衰减
def train(lambd):
w, b = init_params()
#linreg和squared_loss和sgd在之前进行定义
#
net, loss = lambda X: linreg(X, w, b), squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())
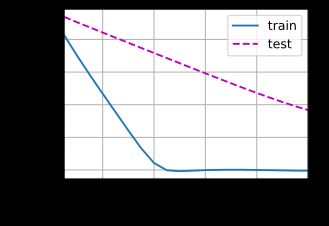
我们现在用lambd = 0禁用权重衰减后运行这个代码。 注意,这里训练误差有了减少,但测试误差没有减少, 这意味着出现了严重的过拟合。
train(lambd=0)
w的L2范数是: 13.111292839050293
下面,我们使用权重衰减来运行代码。 注意,在这里训练误差增大,但测试误差减小。 这正是我们期望从正则化中得到的效果。
train(lambd=3)
w的L2范数是: 0.3369603753089905
4.1.3、使用Pytorch的简洁实现
由于权重衰减在神经网络中很常用,深度学习框架为了便于我们使用权重衰减,将权重衰减集成到优化算法中,以便与任何损失函数结合使用。神经网络的 L 2 L_2 L2正则化称为权重衰减(weight decay)。troch.optim中继承了很有优化器,上节详细介绍了几个,如SGD,Adadelta,Adam,Adagrad,RMSProp等,这些优化器自带的一个参数weight_decay用于指定权值衰减率,相当于 L 2 L_2 L2正则化中的 λ \lambda λ参数。
L ( w , b ) + λ ∥ w ∥ 2 L(w, b) + \lambda \|\boldsymbol{w}\|^2 L(w,b)+λ∥w∥2
这里我们只为权重 w w w设置了weight_decay,所以偏置参数 b b b不会衰减。
def train_concise(wd):
#定义网络
net=nn.Sequential(nn.Linear(num_inputs,1))
for param in net.parameters():
param.data.normal_()
#均方误差损失函数
loss=nn.MSELoss(reduction='none')
num_epochs,lr=100,0.003
#通过设置参数weight_decay设置衰减,偏置参数b没有衰减,只对权重参数w进行衰减
trainer=torch.optim.SGD([
{"params":net[0].weight,'weight_decay':wd},
{"params":net[0].bias}],lr=lr)
animator=d2l.Animator(xlabel='epochs',ylabel='loss',yscale='log',
xlim=[5,num_epochs],legend=['train','test'])
for epoch in range(num_epochs):
for X,y in train_iter:
trainer.zero_grad()
l=loss(net(X),y)
l.mean().backward()
trainer.step()
if (epoch+1)%5==0:
animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),
d2l.evaluate_loss(net,test_iter,loss)))
print('w的L2范数:',net[0].weight.norm().item())
不使用衰减:
train_concise(0)
w的L2范数: 12.565210342407227
使用衰减:
train_concise(3)
w的L2范数: 0.366534024477005
4.2 Dropout正则化
4.2.1、简介
除了权重正则化外,深度学习模型常常使用丢弃法(Dropout)来应对过拟合问题。Dropout的做法是在训练过程中按一定比例(比例参数可设置)随机忽略或屏蔽一些神经元。这些神经元会被随机“抛弃”,也就是说他们在正向传播过程中对于下游神经元的共享效果暂时消失了,反向传播时该神经元也不会有任何权重的更新。所以,通过传播过程,Dropout将产生和 L 2 L_2 L2范数相同的收缩权重的效果。
随着神经网络模型的不断学习,神经元的权值会与整个网络的上下文相匹配。神经元的权重针对某些特征进行优化,进而产生一些特殊化。周围的神经元则会依赖于这种特殊化,但如果过于特殊化,模型会因为对训练数据的过拟合而变得脆弱不堪。加入了Dropout以后,输入的特征都是有可能会被随机清除的,所以该神经元不会再特别依赖于任何一个输入特征,也就是说不会给任何一个输入设置太大的权重。由于网络模型对神经元特定的权重不那么敏感,因此提升了模型的泛化能力,不容易对训练数据过拟合。
有一个隐藏层5个隐藏单元的多层感知机,当将dropout应用到隐藏层,该层的隐藏单元将有一定的概率被丢弃掉。设丢弃概率为 p p p,那么有 p p p的概率 h i h_i hi会被清零,有 1 − p 1-p 1−p的概率 h i h_i hi会除以 1 − p 1-p 1−p做拉伸。丢弃概率是丢弃法的超参数。因此,每个中间激活值 h h h以丢弃概率 p p p由随机变量 h ′ h^{'} h′替换,如下所示:
h ′ { 0 , 概 率 为 p h 1 − p , 其 他 情 况 h^{'} \begin{cases} 0, & 概率为p \\ \cfrac {h}{1-p}, & 其他情况 \end{cases} h′⎩⎨⎧0,1−ph,概率为p其他情况
根据设计,期望值保持不变,即 E [ h ′ ] = h E[h^{'}]=h E[h′]=h
对左图的隐藏层使用Dropout法,一种可能的结果如右图所示,其中 h 2 h_2 h2和 h 5 h_5 h5被清零。这时输出值的计算不在依赖 h 2 h_2 h2和 h 5 h_5 h5,在反向传播时,与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的,即 h 1 , ⋯ , h 5 h_1,\cdots ,h_5 h1,⋯,h5都有可能被清零,输出层的计算无法过度依赖 h 1 , ⋯ , h 5 h_1,\cdots ,h_5 h1,⋯,h5中的任何一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。
Dropout在训练阶段和测试阶段是不同的,一般在训练中使用,测试时不使用。不过在测试时,为了平衡(因训练时舍弃了部分节点或输出),一般将输出按Dropout Rate比例缩小。
如何或何时使用Dropout?下面是一般原则:
- 通常丢弃率控制在20%~50%比较好,可以从20%开始尝试。如果比例太低则起不到效果,比例太高则会导致模型的欠学习。
- 在大的网络模型上应用:当dropout用在较大的网络模型时,更有可能得到效果的提升,模型有更多的机会学习到多种独立的表征。
- 在输入层和隐藏层都使用dropout。
- 增加学习速率和冲量:把学习速率扩大10-100倍,冲量值调高到0.9-0.99。
- 大的学习速率往往导致大的权重值。对网络的权重值做最大范数的正则化,被证明能提升模型性能。
4.2.2、从零开始实现
要实现单层的dropout函数,必须从伯努利(二元)随机变量中提取与我们的层的维度一样多的样本,其中随机变量以概率 1 − p 1-p 1−p取值1(保持),以概率 p p p取值0(丢弃)。实现这一点的简单方式是首先从均匀分布 U [ 0 , 1 ] U[0,1] U[0,1]中抽取样本。那么就可以保留那些对样样本大于 p p p的节点,把剩下的丢弃。
下面实现dropout_layer函数,该函数以dropout的概率丢弃张量输入X中的元素,如上所述重新缩放剩余部分:将剩余部分除以 1.0 − d r o p o u t 1.0-dropout 1.0−dropout。
import torch
from torch import nn
import torch.nn.functional as F
from d2l import torch as d2l
import torchvision
from torch.utils import data
from torchvision import transforms
def dropout_layer(X,dropout):
assert 0<=dropout<=1
#在该情况下,所有元素都被丢弃
if dropout==1:
return torch.zeros_like(X)
#在该情况下所有元素都被保留
if dropout==0:
return X
#torch.Tensor(X.shape).uniform_(0,1):生成0-1内的随机数,形状与X相同
#大于dropout设置为1,小于等于为0
mask=(torch.Tensor(X.shape).uniform_(0,1)>dropout).float()
return mask*X/(1.0-dropout)
下面通过几个例子来测试dropout_layer函数。在下面的代码中,将输入X通过dropout操作,丢弃率分别为0、0.5、1。
X=torch.arange(16,dtype=torch.float32).reshape((2,8))
print(X)
print(dropout_layer(X,0.))
print(dropout_layer(X,0.5))
print(dropout_layer(X,1.))
tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14., 15.]])
tensor([[ 0., 0., 0., 0., 0., 0., 0., 14.],
[ 0., 18., 0., 0., 0., 0., 28., 30.]])
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0.]])
数据集使用Fashion-MNIST数据集,构建的模型完成多分类任务。
定义的模型是具有两个隐藏层的多层感知机,模型将dropout应用于每个隐藏层的输出(在激活函数之后)。分别为每一层设置丢弃概率。通常在靠近输入层的地方设置较低的丢弃概率。下面将第一个和第二个隐藏层的丢弃概率分别设置为0.2和0.5。并且只在训练期间有效。
dropout1,dropout2=0.2,0.5
class Net(nn.Module):
def __init__(self,num_inputs,num_outputs,num_hiddens1,num_hiddens2,is_training=True):
super(Net, self).__init__()
self.num_inputs=num_inputs
self.training=is_training
self.lin1=nn.Linear(num_inputs,num_hiddens1)
self.lin2=nn.Linear(num_hiddens1,num_hiddens2)
self.lin3=nn.Linear(num_hiddens2,num_outputs)
def forward(self,X):
X=F.relu(self.lin1(X.reshape((-1,self.num_inputs))))
#只有在训练的时候才是用dropout
if self.training==True:
#在第一个全连接层之后添加一个dropout层
X=dropout_layer(X,dropout1)
X=F.relu(self.lin2(X))
if self.training==True:
# 在第二个全连接层之后添加一个dropout层
X = dropout_layer(X, dropout2)
X=self.lin3(X)
return X
#实例化模型
num_inputs,num_outputs,num_hiddens1,num_hiddens2=784,10,256,256
net=Net(num_inputs,num_outputs,num_hiddens1,num_hiddens2)
定义加载Fashion-MNIST数据集的函数,并加载数据集。
#定义加载数据集函数并加载数据集
def load_data_fashion_mnist(batch_size,resize=None):
#下载Fashion-MNIST数据集,然后将其加载到内存中
#ToTensor():将numpy的ndarray或PIL.Image读的图片转换成形状为(C,H, W)的Tensor格式,
trans=[transforms.ToTensor()]
#insert:将数据形状转为规定形状,并用0补充数据
if resize:
trans.insert(0,transforms.Resize(resize))
#Compose将多个步骤组合在一起
trans=transforms.Compose(trans)
mnist_train=torchvision.datasets.FashionMNIST(root="./fashion_mnist_data",train=True,
transform=trans,download=True)
mnist_test=torchvision.datasets.FashionMNIST(root="./fashion_mnist_data",train=False,
transform=trans,download=True)
return (data.DataLoader(mnist_train,batch_size,
shuffle=True,num_workers=0),
data.DataLoader(mnist_test,batch_size,
shuffle=False,num_workers=0))
batch_size=256
train_iter,test_iter=load_data_fashion_mnist(batch_size)
定义与模型训练相关的函数,并对模型进行训练。
#训练轮次和学习率
num_epochs,lr=10,0.5
#交叉熵损失函数
loss=nn.CrossEntropyLoss()
#SGD优化器
trainer=torch.optim.SGD(net.parameters(),lr=lr)
#计算预测正确的数量
def accuracy(y_hat,y):
if len(y_hat.shape)>1 and y_hat.shape[1]>1:
y_hat=y_hat.argmax(axis=1)
cmp=y_hat.type(y.dtype)==y
return float(cmp.type(y.dtype).sum())
#用于对多个变量进行累加
class Accumulator:
def __init__(self,n):
self.data=[0.0]*n
def add(self,*args):
self.data=[a+float(b) for a,b in zip(self.data,args)]
def reset(self):
self.data=[0.0]*len(self.data)
#可以通过索引获取数据
def __getitem__(self, idx):
return self.data[idx]
#定义一个可以获取任一模型精度的函数
def evaluate_accuracy(net,data_iter):
if isinstance(net,torch.nn.Module):
#将模型设置为评估模式
net.eval()
#正确预测数和预测总数两个变量
metric=Accumulator(2)
with torch.no_grad():
for X,y in data_iter:
metric.add(accuracy(net(X),y),y.numel())
return metric[0]/metric[1]
#训练模型的一个迭代周期
def train_epoch(net,train_iter,loss,updater):
#将模型设置为训练模式
if isinstance(net,torch.nn.Module):
net.train()
#记录损失总和,训练准确度总和,样本数
metric=Accumulator(3)
for X,y in train_iter:
#计算梯度并更新参数
y_hat=net(X)
l=loss(y_hat,y)
if isinstance(updater,torch.optim.Optimizer):
##使用Pytorch内置的优化器和损失函数
updater.zero_grad()
l.sum().backward()
updater.step()
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
#返回训练损失和训练精度
return metric[0]/metric[2],metric[1]/metric[2]
#训练模型
def train(net,train_iter,test_iter,loss,num_epochs,updater):
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0, 1],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics=train_epoch(net,train_iter,loss,updater)
test_acc=evaluate_accuracy(net,test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
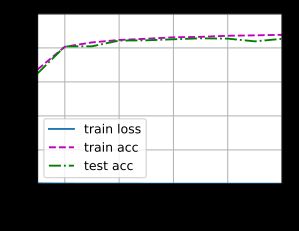
train(net,train_iter,test_iter,loss,num_epochs,trainer)
4.2.3、简洁实现
在pytorch中,只需要在全连接层之后添加一个Dropout层,将丢弃概率作为唯一的参数传递给他的构造函数。
dropout1,dropout2=0.2,0.5
class Net1(nn.Module):
def __init__(self,num_inputs,num_outputs,num_hiddens1,num_hiddens2,is_training=True):
super(Net1, self).__init__()
self.num_inputs=num_inputs
self.training=is_training
self.lin1=nn.Linear(num_inputs,num_hiddens1)
self.lin2=nn.Linear(num_hiddens1,num_hiddens2)
self.lin3=nn.Linear(num_hiddens2,num_outputs)
self.dropout1=nn.Dropout(dropout1)
self.dropout2 = nn.Dropout(dropout2)
def forward(self,X):
X=F.relu(self.lin1(X.reshape((-1,self.num_inputs))))
#只有在训练的时候才是用dropout
if self.training==True:
#在第一个全连接层之后添加一个dropout层
X=self.dropout1(X)
X=F.relu(self.lin2(X))
if self.training==True:
# 在第二个全连接层之后添加一个dropout层
X = self.dropout2(X)
X=self.lin3(X)
return X
num_inputs,num_outputs,num_hiddens1,num_hiddens2=784,10,256,256
net1=Net1(num_inputs,num_outputs,num_hiddens1,num_hiddens2)
#训练轮次和学习率
num_epochs,lr=10,0.5
#加载训练和测试所使用的的数据。
batch_size=256
train_iter,test_iter=load_data_fashion_mnist(batch_size)
#交叉熵损失函数
loss=nn.CrossEntropyLoss()
#SGD优化器
trainer=torch.optim.SGD(net1.parameters(),lr=lr)
train(net1,train_iter,test_iter,loss,num_epochs,trainer)