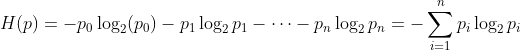决策树模型
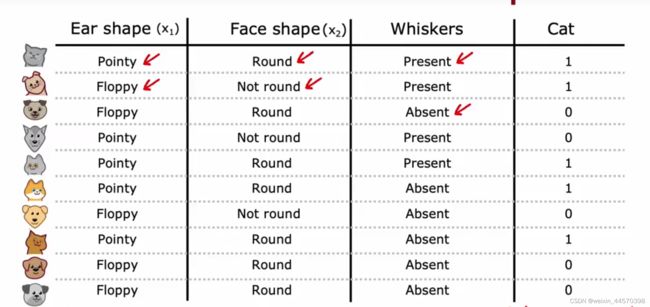
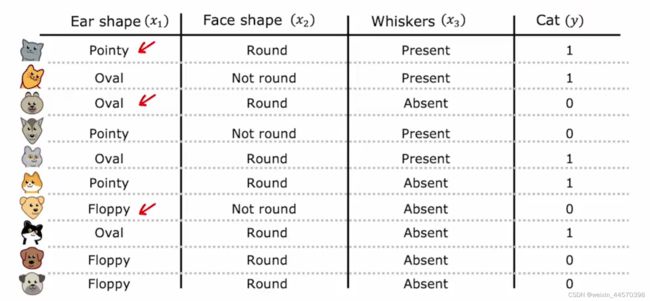
有如下图所示的动物分类例子,有三个输入特征![]() ,
,![]() 和
和![]() ,分别是耳朵的形状,脸型和是否有胡须,每个特征都是一个二元的离散值,需要预测的目标变量
,分别是耳朵的形状,脸型和是否有胡须,每个特征都是一个二元的离散值,需要预测的目标变量![]() 是这只动物是否是一只猫,若是,则输出
是这只动物是否是一只猫,若是,则输出![]() ,否则输出
,否则输出![]() ,所以这是一个二元分类。
,所以这是一个二元分类。
根据这个问题可以构建一颗简单的决策树(Decision Tree),决策树的非叶节点称为决策节点(decision node) ,为输入特征,叶子节点为目标变量,在这个例子里就是该动物是否是一只猫。
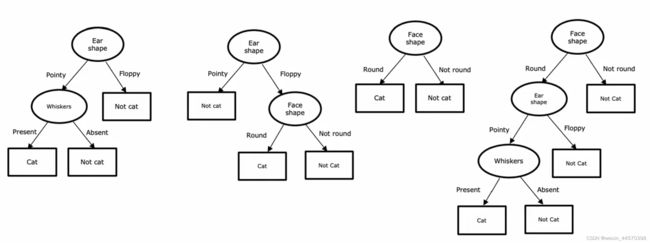
以下都是尝试对该动物分类的决策树模型,有些可能在训练集上表现得很好,但有些可能效果很差,决策树学习算法的工作就是在所有可能的决策树中,选择一个在训练集上表现良好,且有很强泛化性的模型。所以该如何根据输入特征去构建一颗决策树?
目录
1、纯度
2、特征的值
2.1、独热编码(One-hot)
2.2、连续的特征值
3、随机森林
4、回归树
1、纯度
如何在每个节点选择哪些特征来进行拆分,我们希望在对该特征进行拆分以后尽可能地提高拆分后子集的纯度,如果子集中只包含猫或者全不是猫,那么说明该子集纯度很高,反之如果都混在一起,则纯度很低,为了具体说明纯度,引入“熵(Entropy)”的概念,熵是衡量一组数据是否纯的指标。
给定以下例子,定义![]() 为猫样本在训练集中的比例,既分类为
为猫样本在训练集中的比例,既分类为![]() 的比例,在这个例子中
的比例,在这个例子中
![]()
![]()
现在定义熵为![]() 是关于任一分类
是关于任一分类![]() 在训练集中的比例,既
在训练集中的比例,既![]() 的曲线,下图是
的曲线,下图是![]() 的图像。
的图像。
从图中可以得出,当![]() 时,熵
时,熵![]() 最大为1,说明最不纯,因为训练集中猫和非猫的比例各占一半。而无论拆分后的子集中猫的比例增大,或是非猫的比例增大,都说明该子集的纯度在提高,熵在变小。我们选择的拆分方式就是尽可能地可以使子集纯度更高,熵更小。
最大为1,说明最不纯,因为训练集中猫和非猫的比例各占一半。而无论拆分后的子集中猫的比例增大,或是非猫的比例增大,都说明该子集的纯度在提高,熵在变小。我们选择的拆分方式就是尽可能地可以使子集纯度更高,熵更小。
以二元分类为例,熵函数![]() 为
为
![]()
当![]() 时,既训练集中没有猫时,说明纯度很高,熵很小
时,既训练集中没有猫时,说明纯度很高,熵很小
又因为
![]()
所以![]() 可以化简为
可以化简为
![]()
因此![]() 元分类的熵
元分类的熵![]() 为
为
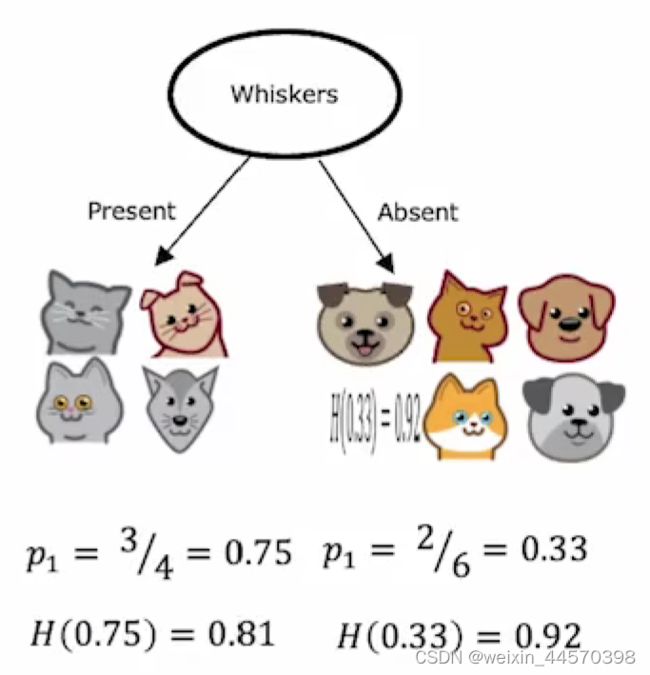
在节点上拆分什么特征将取决于选择什么特征可以最大程度的减小熵,在决策树的学习中,熵的减少被称为信息增益(information gain)。依次把每一个特征作为根节点来进行分割训练集,还是以猫分类为例,当选择用![]() 耳朵形状作为根节点来分割训练集时
耳朵形状作为根节点来分割训练集时
左子树5个,右子树5个,左子树非猫1个![]() ,猫4个
,猫4个![]() ,根据熵的公式
,根据熵的公式
![]()
![]()
当分别选用![]() 脸型和
脸型和![]() 是否有胡须作为根节点来划分训练集时,
是否有胡须作为根节点来划分训练集时,
对比三种划分方式,选择熵减少最多的一个一个特征来划分数据集。如何观察每一次的划分的信息增益?将左右子树的熵加权求出平均熵值,再求出其父节点的熵,将两个值相减,在这个例子中左右子树的父节点就是根节点。
根节点的熵为
![]()
信息增益分别为
它衡量的就是每次划分熵的减少,因此选择![]() 耳朵形状来划分,熵减少的最多,在每一层都进行上述操作。
耳朵形状来划分,熵减少的最多,在每一层都进行上述操作。
信息增益不仅帮助我们选取用于划分的特征,还可以用于决定何时停止划分,当划分完成后信息增益很小时,应该考虑是否不再增加树的高度,或者是否会有过拟合的风险。
把每一层左子树分类![]() 在子集中的比例记作
在子集中的比例记作![]() ,右子树分类
,右子树分类![]() 在子集中的比例记作
在子集中的比例记作![]()
![]()
![]()
父类节点分类![]() 在子集中的比例记作
在子集中的比例记作![]() ,而根节点分类
,而根节点分类![]() 在子集中的比例记作
在子集中的比例记作![]()
从上一层父节点划分到左子树的样本个数,既左子树的权值记作![]() ,划分到右子树的样本个数,既右子树的权值记作
,划分到右子树的样本个数,既右子树的权值记作![]() ,因此信息增益一般形式可以表示为
,因此信息增益一般形式可以表示为
![]()
2、特征的值
2.1、独热编码(One-hot)
在之前的例子中,每个特征可以选择的值都只有两个中的一个,脸是圆的或者不圆的,有没有胡须等,但是有时特征可能会采用两个以上离散的值,比如说脸是圆的,椭圆的或者方的。这时可以把这一个采用多个离散值的特征拆分为多个特征,每个特征都只采用两个离散值,既
![]()
把![]() 拆分为
拆分为![]() 个特征,每个特征只包含两个离散的值
个特征,每个特征只包含两个离散的值
![]()
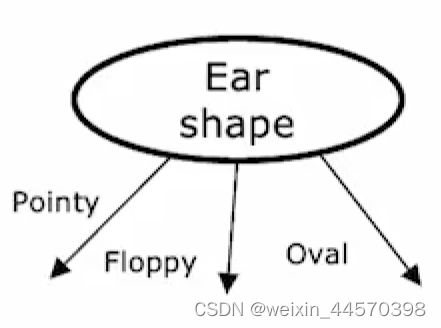
如下图所示,特征![]() 耳朵的形状,由原来只采用尖的和软的两个离散的值,变为尖的,圆的和软的三个离散的值
耳朵的形状,由原来只采用尖的和软的两个离散的值,变为尖的,圆的和软的三个离散的值
当然也可以根据每个特征所采用的离散值的个数![]() ,来拆分数据集,构造
,来拆分数据集,构造![]() 叉树。此时
叉树。此时![]() 采用了三个离散值,因此构造一棵三叉树
采用了三个离散值,因此构造一棵三叉树
这里选择采用独热编码的方式,将![]() 耳朵形状拆分成三个新的特征,
耳朵形状拆分成三个新的特征,![]() ,
,![]() 和
和![]() ,每个特征的值都是原来的特征可以取到的值,采用两个离散的值 表示是和否,既0和1。
,每个特征的值都是原来的特征可以取到的值,采用两个离散的值 表示是和否,既0和1。
2.2、连续的特征值
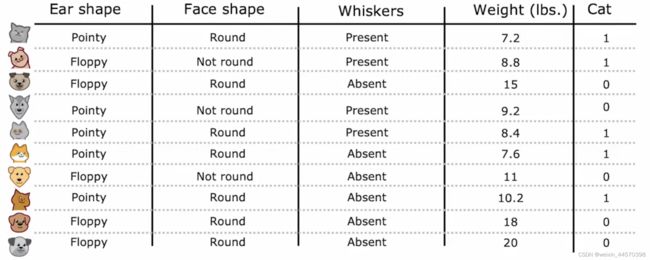
之前选取的特征都只采用了离散的值,当输入特征包含连续的值的时候,该怎么对这些值进行处理。如下图所示,给之前猫分类的例子加上了新的特征![]() ,既体重,体重是一个连续的值。
,既体重,体重是一个连续的值。
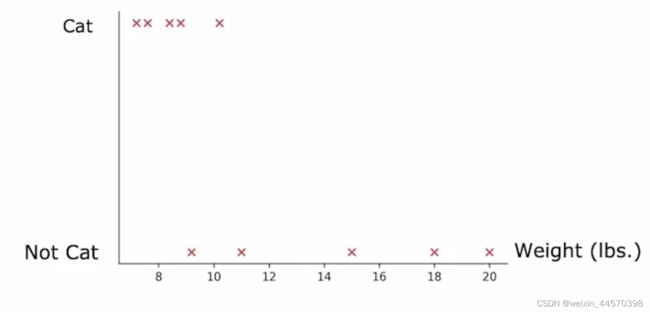
可以根据这些连续的值画出对应的离散点,选取一个阈值,根据这个阈值来划分数据集,并且能带来最好信息增益。
假设阈值选8,那么左子树有两只猫,右子树有三只猫和五只狗,信息增益为
假设阈值选为9,那么左子树有四只猫,右子树有一只猫和五只狗,信息增益为
假设阈值选为13,那么左子树有五只猫和两只狗,右子树有三只狗,信息增益为
选取能使信息增益最大的阈值9,当![]() 时划分为左子树,
时划分为左子树,![]() 时划分为右子树。
时划分为右子树。
3、随机森林
如果我们利用训练集只构造一棵决策树,当训练集中改变一个样本的时候,决策树的划分方式可能就会发生很大的变化,所以我们需要构造多个决策树,最后对新样本进行预测时就选取预测次数最多的那一个类别。
需要构造多个决策树,就需要多个训练集,我们对原有的训练集进行有放回抽样(sampling with replacement),重复若干次,一般不会超过100次,就会得到若干个训练集,再利用其构造多个决策树。
在构造决策树时,可能包含![]() 个输入特征,这会导致在选取划分特征的时候依然会有很高的重复率而且时间开销很大,因此选取划分特征时在
个输入特征,这会导致在选取划分特征的时候依然会有很高的重复率而且时间开销很大,因此选取划分特征时在![]() 个特征中选取信息增益最大的特征,
个特征中选取信息增益最大的特征,![]() ,一般
,一般
![]()
或者
![]()
这些决策树就被称为随机森林(random forest)。
4、回归树
对于回归问题也可以利用决策树来进行预测,在解决分类问题时,信息增益是
![]()
而在解决回归问题是,不在利用熵去检验子集的纯度,而是利用方差检验数据的离散程度。因此,信息增益为
![]()
![]() 为节点的方差,选择信息增益最大特征进行划分,参数
为节点的方差,选择信息增益最大特征进行划分,参数![]() 和
和![]() 不变。
不变。