常用相机投影及畸变模型（针孔|广角|鱼眼）

Reference:

1. 高翔，张涛 《视觉SLAM十四讲》
2. 鱼眼镜头是怎么「鱼眼」的？
3. VIO标定（二）广角相机模型
4. 鱼眼相机模型EUCM（一）
5. 相机模型–Omnidirectional Camera
6. Omnidirectional Camera
7. Mei: http://www.robots.ox.ac.uk/~cmei/articles/single_viewpoint_calib_mei_07.pdf
8. OCamCalib: Omnidirectional Camera Calibration Toolbox for Matlab

omnidirectional camera（广角相机）：在一个水平面有360°视野的相机，或视野能覆盖半个球或近似整个球的相机。

1. 背景

面镜(mirror)与透镜(lens)的区别：

• 面镜用的是镜面反射；
• 透镜用的是镜面折射。

广角相机成像步骤与普通相机基本一致，主要的区别在于镜头聚光的部分，广角相机为了获得更大的FOV，有三种镜头聚光方式:

1. Dioptric(折射光学的) camera：通过透镜来实现，主要是折射；仅通过折射，比如鱼眼镜头
2. Catadioptric(反射折射的) camera：使用一个标准相机和一个面镜 shaped mirror — such as a parabolic, hyperbolic, or elliptical mirror，后面介绍的mirror都是如此，其在水平面可以提供360度视野，仰角方向大于100度;
3. Poly-dioptric camera：通过组合多个相机来重叠相机视野。

2. 针孔相机投影模型及其畸变模型

设$O-x-y-z$为相机坐标系，习惯上将$z$轴指向相机前方，$x$轴向右，$y$轴向下。$O$为摄像机的光心，也是针孔模型中的针孔。现实世界的空间点P，经过小孔$O$投影之后，落在物理成像平面$O^{\prime }-x^{\prime }-y^{\prime }$上，成像点为$P^{\prime }$。
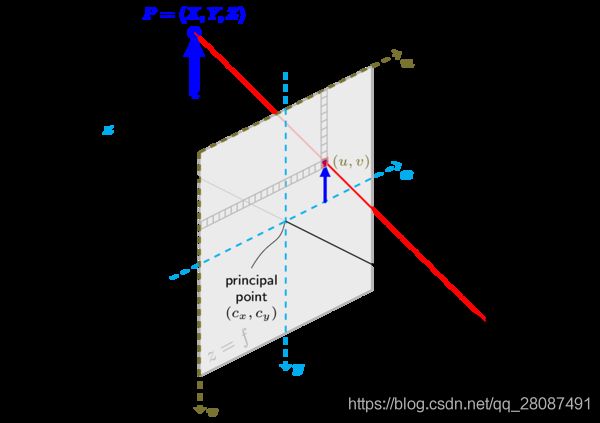(注意这里的 $(c_x,c_y)$ 写的是 光心 或 principle point(PP)，不是畸变中心(COD)！)

2.1 缩略词和术语

Term	Description
COD	畸变中心(Center of Distortion) - 在传感器上的 $(x,y)$ 表示拟合的最佳对称中心 (unit:pixel)
DM	畸变模型(Distortion Model)
EFL	有效焦距(Effective Focal Length)
Pinhole Model FL	针孔模型焦距(Pinhole Model Focal Length) - 图像去畸变后的模型焦距 (unit:pixel)
FOV	视野(Field of View)
PP	主点(Principle Point) - 透镜光轴与传感器表面的交点
LPP	透镜主平面(Lens Primary Plane)

2.1 世界坐标系到像素坐标系

世界坐标系中三维点$M=[X,Y,Z{]}^T$和像素坐标系中二维点$m=[u,v{]}^T$的关系为：
$$s\tilde{m}=A[Rt]\tilde{M}$$

即：
$$s\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=Z_c\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{lll}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{lll}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{llll}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

其中，$s$为缩放因子($Z_c$)，$A$为相机的内参矩阵，$[Rt]$ 为相机的外参矩阵，$\tilde{m}$ 和 $\tilde{M}$ 分别为 $m$ 和 $M$对应的齐次坐标系。

2.2 针孔相机模型

相机将三维世界中的坐标点(unit: m) 映射到二维图像平面(unit: pixel) 的过程能够用一个几何模型来描述，其中最简单的称为针孔相机模型 (pinhole camera model)。

2.2.1 世界坐标系到相机坐标系

$$\left[\begin{array}{l}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+t=[Rt]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{llll}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

2.2.2 相机坐标系到像素坐标系

根据三角形相似关系，有：
$$\frac{Z_c}{f}=\frac{X_c}{x}=\frac{Y_c}{y}$$

整理，得：
$$\{\begin{array}{l}x=f\cdot \frac{X_c}{Z_c}\\ y=f\cdot \frac{Y_c}{Z_c}\end{array}$$

像素坐标系通常的定义方式是：原点 $o^{\prime }$ 位于图像的左上角，$u$ 轴向右与 $x$ 轴平行，$v$ 轴向下与 $y$ 轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的位移。我们设像素坐标在 $u$ 轴上缩放了 $\alpha$ 倍，在 $v$ 轴上缩放了 $\beta$ 倍。同时，原点平移了 $[c_x,c_y{]}^T$。那么整理得，坐标之间的关系为：
$$\{\begin{array}{l}u=\alpha \cdot x+c_x\\ v=\beta \cdot y+c_y\end{array}⟹\{\begin{array}{l}u=\alpha f\cdot \frac{X_c}{Z_c}+c_x=f_x\frac{X_c}{Z_c}+c_x\\ v=\beta f\cdot \frac{Y_c}{Z_c}+c_y=f_y\frac{Y_c}{Z_c}+c_y\end{array}$$

其中，

• $f$ 为镜头焦距，单位为米;
• $\alpha$、$\beta$ 的单位为像素/米;
• $f_y$、$f_y$​ 为 $x$、$y$ 方向的焦距，单位为像素。

最终，写成矩阵的形式为：
$$Z_c\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}{X}_c\\ Y_c\\ Z_c\end{array}\right]=KP$$

2.3 综述

从另一个角度看，我们可以把一个世界坐标点先转换到相机坐标系，再除掉它最后一维的数值（即该点距离相机成像平面的深度），这相当于把最后一维进行归一化处理，得到点 $P$ 在相机归一化平面上的投影：
$$(R{P}_w+t)=[X,Y,Z{]}^T(相机坐标)\to [X/Z,Y/Z,1{]}^T（归一化坐标）$$

归一化坐标可以看成相机前方 $z=1$ 处的平面上的一个点，这个 $z=1$ 平面也称为归一化平面。归一化坐标再左乘内参就得到了像素坐标，所以我们可以把像素坐标 $[u,v{]}^T$ 看成对归一化平面上的点进行量化测量的结果。从这个模型中也可以看出，如果对相机坐标同时乘以任意非零常数，归一化坐标都是一样的，这说明点的深度在投影过程中被丢失了，所以单目视觉中没法得到像素点的深度值。

2.4 内参标定

内参标定(Intrinsic Camera Calibration) 是找到一个相机的物理参数的过程。标定结果是一个相机内参集合。

2.5 畸变模型

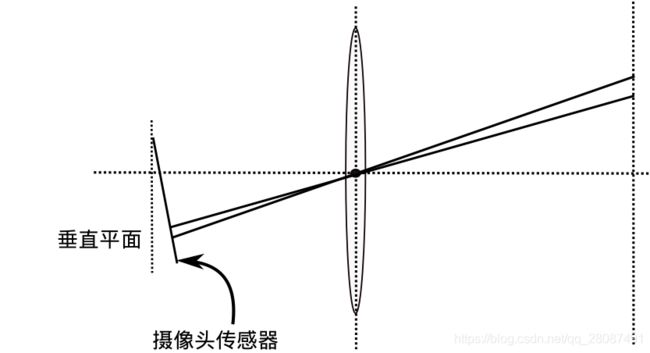
普通相机畸变通常包括径向畸变和切向畸变。如下图所示
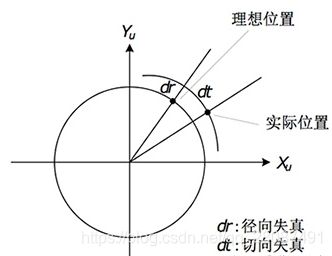切向畸变表达式沿半径方向的偏移量，径向畸变的形成原因是镜头制造工艺不完美，使得镜头形状存在缺陷，通常又分为桶性畸变和枕形畸变，分别代表 $dr$ 往外偏和往里偏。

$[x_{distorted},y_{distorted}{]}^T$是畸变后点的归一化坐标。

2.5.1 径向畸变

真实的摄像头使用的并不是针孔，它们使用的是能一次性聚焦大量光线的镜头，这使得其能迅速生成图像，但是，镜头仍会产生失真，光线通常会在摄像机镜头的边缘出现较大或较小幅度的弯曲，这会产生图像边缘扭曲的效果，因此，线条或者物体会比真实情况呈现出或多或少的弯曲。这种失真被称为径向畸变，是最常见的失真类型。

实际情况中我们常用 $r=0$ 处的泰勒级数展开的前几项来近似描述径向畸变，径向畸变后的归一化坐标为：
$$\{\begin{array}{l}{x}_{\text{distorted}}=x\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)\\ y_{\text{distorted}}=y\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)\end{array}$$

2.5.2 切向畸变

切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致（相机的组装过程中由于不能使得透镜和成像面严格平行），切向畸变需要两个额外的畸变参数来描述，切向畸变后的归一化坐标为：
$$\{\begin{array}{l}{x}_{\text{distorted}}=x+2p_{1}xy+p_2\left(r^2+2x^2\right)\\ y_{\text{distorted}}=y+2p_{2}xy+p_1\left(r^2+2y^2\right)\end{array}$$

其中，$r^2=x^2+y^2$。
对于相机坐标系中的一点 $P$，我们能够通过5个畸变系数找到这个点在像素平面上的正确位置：
$$\{\begin{array}{l}{x}_{\text{distorted}}=x\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)+2p_{1}xy+p_2\left(r^2+2x^2\right)\\ y_{\text{distorted}}=y\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)+2p_{2}xy+p_1\left(r^2+2y^2\right)\end{array}$$

由于参数过多导致数值求解不稳定, 通常只使用$k_1$,$k_2$,$k_3$,$p_1$,$p_2$综上，我们一共需要5个畸变参数$\left(k_1,k_2,k_3,p_1,p_2\right)$来描述透镜畸变。
将畸变后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置：
$$\{\begin{array}{l}u=f_x{x}_{\text{distorted}}+c_x\\ v=f_y{y}_{\text{distorted}}+c_y\end{array}$$

2.5.3 歪斜（skewed）

图像传感器图像原尺寸在制造过程可能不是正方形，同时可能存在歪斜（skewed）(也就是物理成像平面可能在设计或生产上是个歪的)，因此需要考虑这些影响因素，传感器歪斜和不是正方形主要对相机 $x$ 和 $y$ 方向的焦距产生影响。

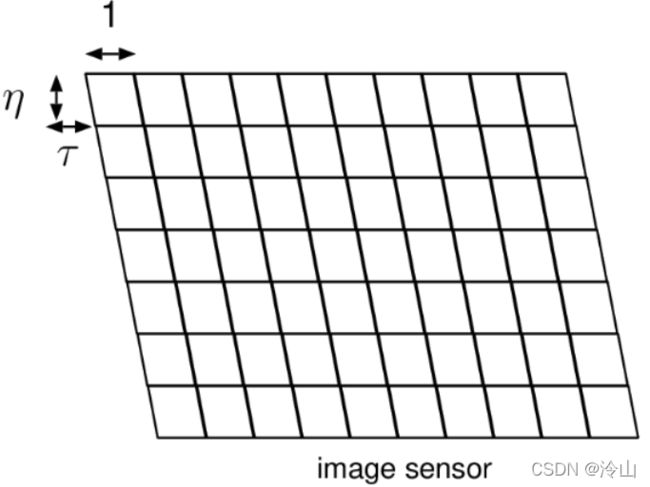
在不考虑畸变的情况下，考虑主点偏移、图像传感器的特性，3D 目标点成像数学模型用以下公式可完全表达。这就是相机内部参数对成像的影响，因此 $K$ 称为内参矩阵，相机内参标定主要是标定相机的焦距、主点、歪斜(下面的$s$)等内部参数。
$$Z_c\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& s& c_x\\ 0& \eta f& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}{X}_c\\ Y_c\\ Z_c\end{array}\right]=KP$$

2.6 畸变矫正

将图像中的每个位置，在畸变后的位置找出。

for (int v = 0; v < height; v++) {
  for (int u = 0; u < width; u++) {

    double u_distorted = 0, v_distorted = 0;

	// 计算点(u,v)对应到畸变图像中的坐标(u_distorted, v_distorted)
    double x = (u-cx)/fx;
    double y = (v-cy)/fy;

    double x2 = x*x, y2 = y*y, xy = x*y, r2 = x2 + y2;
    double x_radial = x * (1 + k1*r2 + k2*r2*r2);
    double y_radial = y * (1 + k1*r2 + k2*r2*r2);
    double x_tangential = 2*p1*xy + p2*(r2 + 2*x2);
    double y_tangential = 2*p2*xy + p1*(r2 + 2*y2);
    double xd = x_radial + x_tangential;
    double yd = y_radial + y_tangential;

    u_distorted = xd*fx + cx;
    v_distorted = yd*fy + cy;

    // 赋值(最近邻插值)
    if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < width && v_distorted < height)
        img_dst(v, u) = (*this)((int) v_distorted, (int) u_distorted);
    else
        img_dst(v, u) = 0;
  }
}

2.7 COD 和 PP

以下为 COD 和 PP 误差示意图：

(注意COD图片上两点在透镜中心相交，而PP的理论上垂直于传感器表面。也就是说在透镜装歪了的时候，COD本身也会跟着歪过来，但是PP理论上是垂直的，可能因为标定误差的原因导致它偏离了原位置)

有些情况下 PP 和 COD 是相似的，有些情况下它们可能是不同的。这主要取决于 相机构造质量 还有 相机透镜和传感器之间的对齐精度(见下面的一个例子展示了切向失真，这会导致 PP 和 COD 不同)：

2.7.1 除法畸变模型(Division distortion model)

$R_u=R_d/\left(1+\mathrm{sign}\left(K_1\right)\ast {\left(K_1\ast R_d\right)}^2+\mathrm{sign}\left(K_2\right)\ast {\left(K_2\ast R_d\right)}^4+\dots +\mathrm{sign}\left(K_n\right)\ast {\left(K_n\ast R_d\right)}^{2n}\right)$

• $R_u$：去畸变后的半径；
• $R_d$：畸变半径。

2.7.2 除法畸变模型参数

Parameter	Description	Example
camK	最前面的两个参数对应于焦距 x 和焦距 y(像素单位，原始图像)。在大多数情况下，焦距 x 和 y 是相同的，因为传感器像素通常是正方形而不仅仅是矩形。 第三个参数为 skew，通常使用的 skew=0。非零值意味着像素是一个平行四边形，而不是一个完美的矩形/正方形。 第四和第五个参数是主点的坐标PPx和PPy(像素单位，原始图像)	camK = 2612.70312 2612.70312 0 671.287598 277.750671
DM	第一个参数为模型类型。这里 $3$ 代表的是当前使用的是除法模型：$R_u=R_d/(1+\mathrm{sign}\left(K_1\right)\ast {\left(K_1\ast R_d\right)}^2+\mathrm{sign}\left(K_2\right)\ast {\left(K_2\ast R_d\right)}^4+\mathrm{sign}\left(K_3\right)\ast {\left(K_3\ast R_d\right)}^6)$ 第2和第3个参数是畸变中心的坐标CODx和CODy。 参数4到6是畸变系数，为上面的公式 $K$ 的 $1-3$。 最后一个参数是 $\gamma$，总是 $1$。	distortParams = 3 635.07196 560.289429 -0.000464434823 0.000386408938 0.000644135347 1

2.8 针孔相机成像过程建模总结

3. 广角相机理论知识

3.1 Central omnidirectional cameras

一个视觉系统是 central 的话，那么被观测物体的所有入射光线汇交于 $3D$ 空间的一个点，这个点称为映射中心 (projection center)或单一有效视野点 (single effective viewpoint)。这个特性被称为单一有效视点特性。透视相机是中心投影系统的一个例子，因为不同的光线相交于一点，即相机的光学中心。
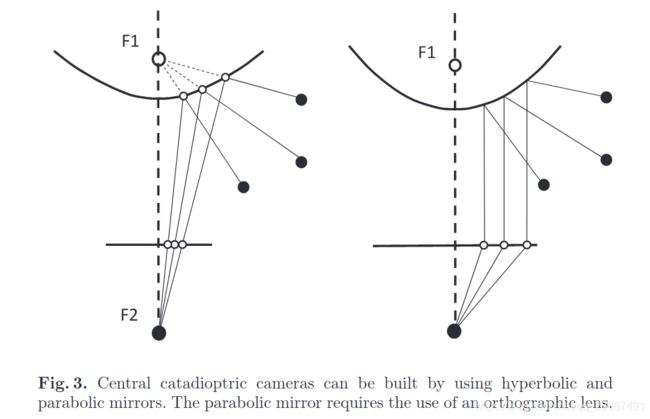
所有的现代鱼眼摄像机都是 central 的，因此，它们满足单一有效视点特性(只是说满足单一有效视点特性，注意不是说现代鱼眼相机是通过镜面反射的-----即满足单一有效视点特性，就可以拟合类似的模型)。Central catadioptric cameras 由一个相机加上一个面镜所组成(如图，相机为底下成像平面，面镜为上面反射的mirror)，相机和面镜的距离需要选择合适。面镜的家族里，能满足单一有效视野点特性的有 hyperbolic, parabolic, and elliptica 面镜。

• Camera + hyperbolic mirror | Camera + parabolic mirror + orthographic lens
  在 hyperbolic 和 elliptical 面镜的情况下，单一有效视点特性是通过确保相机中心(针孔或透镜的中心)正值双曲线(椭圆)的焦点之一。在抛物(parabolic)面镜的情况下，必须在面镜和相机间插入一个直角的镜头，这使它可能平行光线反射抛物面镜收敛于摄像机中心：
  
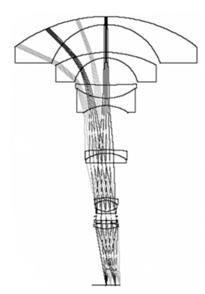
• Camera + fisheye lens
  另一种不使用面镜来扩大摄像机FOV的方法是在摄像机CCD上方增加一个鱼眼镜头。鱼眼镜头是一种能将相机的FOV扩大到190°的镜头系统。如下图所示：
  

3.2 单一有效视点特性为何重要

1. 它允许用户从广角相机捕获的图片生成几何正确的透视图像。因为在单一有效视点约束下，感知图像中的每个像素测量光在一个特定方向通过视点的辐照度。当全向摄像机的几何位置已知时，也就是当摄像机被标定时，我们可以为每个像素预先计算这个方向。因此，可以将每个像素测量的辐照度值映射到距离视点任意距离的平面上，形成平面透视图像。此外，图像可以映射到以单个视点为中心的球体上，即球面投影。
2. 它允许用户应用著名的对极几何理论，这对于sfm来说是非常重要的。对极几何适用于任何 central 相机，无论是 perspective 还是 omnidirectional。

3.3 Unified model for central catadioptric cameras

直观上，有单一有效视点的折射反射模型相比标准透视相机会复杂一些。这个模型确实应该考虑到在折反射照相机的情况下由面镜操作带来的反射，或者在鱼眼照相机的情况下由透镜引起的折射。

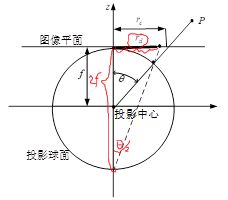
Geyer和Daniilidis证明，每个折射反射的(parabolic, hyperbolic, elliptical) 和标准透视投影相当于从一个集中在单一视点的球体投影映射，到一个与球心垂直距离为$ϵ$ (同后面的$\xi$) 的投影平面。（MEI模型理论）

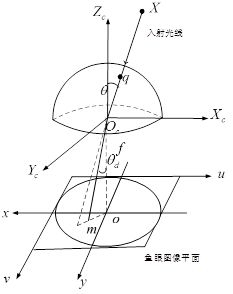
投影模型有四个步骤。令 $P=(x,y,z)$ 为在面镜参考坐标系下以 $C$ 为中心点的场景点。为方便起见，我们假设面镜的对称轴与相机的光轴完全对齐。我们还假设相机和面镜的 $x$ 轴和 $y$ 轴是对齐的。因此，摄像机和面镜参考系之间的差异仅在于沿 $z$ 轴的平移。

1. 将场景点投影在单位球体上，得到：
   $$P_s=\frac{P}{\Vert P\Vert }=\left(x_s,y_s,z_s\right)$$

2. 点坐标被改变为一个新的以 $C_{ϵ}=(0,0,-ϵ)$ 为中心的参考系，因此：
   $$P_{ϵ}=\left(x_s,y_s,z_s+ϵ\right)$$

   $ϵ$ 的范围通常在0 (planar mirror) 和 1 (parabolic mirror)之间。正确的 $ϵ$ 的值可以通过 d:distance between focal points 和 l:the latus rectum 得到。

3. $P_{ϵ}$ 之后被映射到了与 $C_{ϵ}$ 距离为 $1$ 的归一化平面(同针孔模型归一化坐标)，因此：
   $$\tilde{m}=\left(x_m,y_m,1\right)=\left(\frac{x_s}{z_s+ϵ},\frac{y_s}{z_s+ϵ},1\right)=g^{-1}\left(P_s\right)$$

4. 最后，将点 $\tilde{m}$ 映射到相机图像点 $\tilde{p}=(u,v,1)$，通过内参矩阵 $K$，因此：
   $$\tilde{p}=K\tilde{m}$$
   其中$K$为($\theta$ 为倾角，一般为 0)：
   $$K=\left[\begin{array}{ccc}{\alpha }_u& {\alpha }_u\cot (\theta )& u_0\\ 0& {\alpha }_v& v_0\\ 0& 0& 1\end{array}\right]$$

   很容易证明 $g^{-1}$ 是双射的 (正反向一一对应)，它的逆 $g$ 为:
   $$P_s=g(m)\propto \left[\begin{array}{c}{x}_m\\ y_m\\ 1-ϵ\frac{x_m^2+y_m^2+1}{ϵ+\sqrt{1+\left(1-{ϵ}^2\right)\left(x_m^2+y_m^2\right)}}\end{array}\right]$$

   $\propto$表明 $g$ 与右边的式子成正比。要得到归一化因子，只要在单位球体上归一化 $g(m)$ 就足够了。因为 $P_s$ 在单位圆上，因此 $x_s^2+y_s^2+z_s^2=1$。推导过程可见 Section 3.4。

这个函数是 central cata-dioptric cameras 投影模型的核心。它表示了归一化图像平面上的点 $m$ 与面镜参考系中单位向量 $P_s$ 的关系。注意在平面面镜的情况下，我们有 $ϵ=0$，透视相机的投影方程为：$P_s\propto \left(x_m,y_m,1\right)$。

这个模型被证明可以准确描述所有的 central catadioptric cameras (parabolic, hyperbolic, elliptical mirror) 和标准透视相机。这种模型有对鱼眼的扩展，然而，通过折射光近似的鱼眼相机只能在有限的精度上有效。这主要是因为，虽然三种central catadioptric cameras 可以通过精确的参数函数(抛物线、双曲线、椭圆)来表示，但鱼眼镜头的投影模型因相机而异，并取决于镜头的视场。

3.4 全向模型(Omnidirectional)

全向模型利用面镜(mirror)反射进行成像的相机使用的模型。该模型带有一个参数 $\xi$.
首先将相机坐标系的点归一化到半径为1的球面上:
$$\left(\begin{array}{l}{x}_s\\ y_s\\ z_s\end{array}\right)=\frac{1}{\sqrt{x_c^2+y_c^2+z_c^2}}\left(\begin{array}{l}{x}_c\\ y_c\\ z_c\end{array}\right)$$

然后再投影到图像平面上：
$$x_u=\frac{x_s}{z_s+\xi },y_u=\frac{y_s}{z_s+\xi }$$
其逆变换推导出来如下：
$$\begin{gathered} \begin{array}{c}\sqrt{x_s^2+y_s^2+z_s^2}=1\\ \Rightarrow x_u^2{\left(z_s+\xi \right)}^2+y_u^2{\left(z_s+\xi \right)}^2+z_s^2=1\\ \Rightarrow \left(x_u^2+y_u^2+1\right)z_s^2+2\xi \left(x_u^2+y_u^2\right)z_s+x_u^2{\xi }^2+y_u^2{\xi }^2-1=0\end{array} \\ \Rightarrow \left[\begin{array}{l}{x}_s\\ y_s\\ z_s\end{array}\right]=\left[\begin{array}{c}\frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x_u^2+y_u^2\right)}}{x_u^2+y_u^2+1}{x}_u\\ \frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x_u^2+y_u^2\right)}}{x_u^2+y_u^2+1}{y}_u\\ \frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x_u^2+y_u^2\right)}}{x_u^2+y_u^2+1}-\xi \end{array}\right] \end{gathered}$$

最后，注意当 $\xi =0$ 时，全向模型就退化为了针孔模型。
相应的得到归一化平面坐标为：
$$\left[\begin{array}{c}\frac{x_s}{z_s-\xi }\\ \frac{y_s}{z_s-\xi }\\ \frac{z_s}{z_s+\xi }\end{array}\right]=\left[\begin{array}{c}{x}_u\\ y_u\\ 1-\xi \frac{x_u^2+y_u^2+1}{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x_u^2+y_u^2\right)}}\end{array}\right]$$

4. 鱼眼镜头

由于鱼眼镜头会产生极大的形变，因此针孔模型无法为鱼眼镜头建模。鱼眼镜头一般是由十几个不同的透镜组合而成的，在成像的过程中，入射光线经过不同程度的折射，投影到尺寸有限的成像平面上，使得鱼眼镜头与普通镜头相比起来拥有了更大的视野范围。下图表示出了鱼眼相机的一般组成结构。最前面的两个镜头发生折射，使入射角减小，其余的镜头相当于一个成像镜头，这种多元件的构造结构使对鱼眼相机的折射关系的分析变得相当复杂。

研究表明鱼眼相机成像时遵循的模型可以近似为单位球面投影模型。可以将鱼眼相机的成像过程分解成两步：

1. 三维空间点线性地投影到一个球面上，它是一个虚拟的单位球面，它的球心与相机坐标系的原点重合。
2. 单位球面上的点投影到图像平面上，这个过程是非线性的。
   下图表示出了鱼眼相机的成像过程：
   

我们知道，普通相机成像遵循的是针孔相机模型，在成像过程中实际场景中的直线仍被投影为图像平面上的直线。但是鱼眼相机如果按照针孔相机模型成像的话，投影图像会变得非常大，当相机视场角达到180°时，图像甚至会变为无穷大。所以，鱼眼相机的投影模型为了将尽可能大的场景投影到有限的图像平面内，允许了相机畸变的存在。并且由于鱼眼相机的径向畸变非常严重，所以鱼眼相机主要的是考虑径向畸变，而忽略其余类型的畸变。

4.1 投影函数

为了将尽可能大的场景投影到有限的图像平面内，鱼眼相机会按照一定的投影函数来设计。根据投影函数的不同，鱼眼相机的设计模型大致能被分为四种：等距投影模型、等立体角投影模型、正交投影模型和体视投影模型(简单的说，就是把球面上的点一一映射到平面的方法)。下面的四种鱼眼相机的投影模型反映出了空间中的一点 $P$ 是如何投影到球面上，然后到图像平面上成像的。

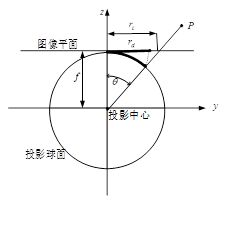
4.1.1 等距投影模型(Equidistant)

公式：$r_d=f\theta$ (距离与 $\theta$ 成正相关，在 $\theta$ 足够小时，可以近似看成是与弧长正相关)
该模型是使用最多的模型，上述式子中，$r_d$ 表示鱼眼图像中的点到畸变中心（画面中心）的距离，$f$是鱼眼相机的焦距，$\theta$是入射光线与鱼眼相机光轴之间的夹角，即入射角。
这种投影方式的特点是，物体在成像平面上离开画面中心的距离，与物体在空间中离开光轴的角度成正比，这个比例系数就是镜头焦距。在这种投影变换下，物体离开中心的距离（角度）就是一个重要的几何性质，物体的空间角距离与物体的像在像平面上的平面距离，是成正比的。这也是这个投影方式名称的来源。在下图的模拟场景中，中间一列的各个小方格的高度都是一样的：

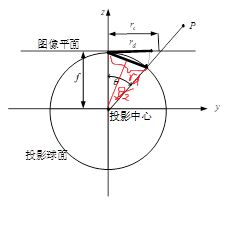
4.1.2 等立体角/等积投影模型(Equisolid Angle/Equal Area)

公式：$r_d=2fsin(\frac{\theta }{2})$
这种投影方式的特征在于，能保持变换前后，物体所占的立体角大小不变。或者说，在半球空间中，半球面上两个面积相同的图案，成像后，在成像平面上的两个图案的面积仍然相同（虽然两者形状不一定相似）。这正式这个投影方式名字的由来。在下图的模拟场景中，圆筒壁上每一列的各个小方格的面积都是相等的：

4.1.3 体视投影/立体投影模型(Stereographic)

公式：$r_d=2ftan(\frac{\theta }{2})$
这种投影方式的特点是能保持角度不变，这在数学上是一个非常良好的性质，叫做保角变换(Conform)。保持角度不变，意思是任何直线相交的角度，在变换之后是保持不变的(虽然直线本身可能变弯曲)。在保角变换下，一个圆仍然还是一个圆(直线可以看做直径无穷大的圆)。所以在某种程度上，保角变换也是保持了「形状」不变的。在下面的模拟场景中，圆筒壁上的所有边界线，全部都变成了圆弧；所有线的交角，也都保持了 90° 不变：

4.1.4 正交投影模型(Orthographic)

公式：$r_d=fsin(\theta )$
这种投影方式，就像是把整个半球直接拍扁，用公式表达就是 r=sin⁡(θ)。在几种投影方式中，这种投影方式带来的扭曲最大，对边缘物体压缩最厉害，实际很少使用。很显然，这种投影方式的最大视场角也不能大于 180°:

4.2 多项式投影模型/Kannala-Brandt Camera Model/KB

对于实际的鱼眼镜头来说，它们不可能精确地按照 4.1 中所述投影模型来设计，所以为了方便鱼眼相机的标定，Kannala 提出了一种鱼眼相机的一般多项式近似模型。通过前面的四个模型，可以发现 $r_d$ 是 $\theta$ 的奇函数，而且将这些式子按泰勒级数展开，发现 $r_d$ 可以用 $\theta$ 的奇次多项式表示，即：
$$r_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+\cdots$$

为了实际计算的方便，需要确定式中 $r_d$ 取到的次幂数。Kannala 提出取式的前五项即取到的九次方，就给出了足够的自由度来很好地近似各种投影模型。$r_d$ 的一次项系数可以为 $1$，于是 OpenCV 中使用的鱼眼相机模型为：
$$r_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+k_4{\theta }^9$$

上式表示的模型是根据四种鱼眼相机投影模型得出的一种通用鱼眼相机多项式模型。这种模型根据 $\theta$ 能够得到 $r_d$，即通过无畸变图像中的点能够计算出鱼眼图像中的畸变点。这种模型在 OpenCV 的鱼眼相机标定方法中是适用的，因为 OpenCV 借助标定板对鱼眼相机进行标定。从空间点到鱼眼图像上的点的变换过程可用式子表示为：
$$\begin{array}{c}\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=RX+t\\ x_c=\frac{X_c}{Z_c},y_c=\frac{Y_c}{Z_c}\\ r^2=x_c^2+y_c^2\\ \theta =\arctan (r)\\ {\theta }_d=k_0\theta +k_1{\theta }^3+k_2{\theta }^5+k_3{\theta }^7+k_4{\theta }^9\\ x_d=\frac{{\theta }_d}{r}{x}_c,y_d=\frac{{\theta }_d}{r}{y}_c\\ u=f_x{x}_d+c_x,v=f_y{y}_d+c_y\end{array}$$

$\theta$ 是入射角，${\theta }_d$ 为畸变后的等效折射角(不是实际的折射角)，$r_d$ 和 ${\theta }_d$ 满足 $r_d=f\cdot tan{\theta }_d$，如果取等效焦距 $f=1$(这里不是实际焦距，而是球面到成像平面使用的距离)，就有 $r_d=tan{\theta }_d$​，考虑到相机的成像CCD平面尺寸一般都是几毫米，焦距在几百毫米左右，所以相机实际成像过程中 ${\theta }_d$ ​是比较小的，${\theta }_d$ 可以近似用 ${\theta }_d$ ​表示($x\to 0$ ，$tanx=x$)，所以才有了等式：
$${\mathrm{r}}_{\mathrm{d}}={\theta }_{\mathrm{d}}=\theta \left(1+{\mathrm{k}}_1{\theta }^2+{\mathrm{k}}_2{\theta }^4+{\mathrm{k}}_3{\theta }^6+{\mathrm{k}}_4{\theta }^8\right)$$

根据相似三角形定理可得(鱼眼镜头的成像原理到畸变矫正(完整版))：
$$\frac{r_d}{r}=\frac{x_d}{x_c}=\frac{y_d}{y_c},x_d=\frac{{\theta }_d}{r}{x}_c,y_d=\frac{{\theta }_d}{r}{y}_c$$

上面式子中，$X$表示空间点，$X_c$表示相机坐标系下对应的空间点，$R$ 和 $t$ 分别是两个坐标系之间的旋转矩阵和平移向量，$(u,v{)}^T$ 表示投影到鱼眼图像上的对应点。OpenCV中对鱼眼相机的标定步骤能够分成四步：（1）初始化内参数；（2）初始化外参数；（3）使用LM算法最小化定位的图像点和投影的图像点之间的投影误差；（4）确定结果。

4.2 UCM (Unified Omnidirectional Camera Model)

该相机模型有5个参数$\left[f_x,f_y,c_x,c_y,\xi \right]$，它刚开始是针对于大FOV的鱼眼相机提出的，并且有两个优点：

1. 它能精确地模拟各种图像设备和畸变的几何图像生成过程
2. 它的反投影是一个闭式解

3D点首先被投影到单位球上，之后单位球上的点在以偏离z轴 $\xi$ 大小为中心的通过针孔模型进行投影，投影的过程可以通过下图进行表示。

4.2.1 投影过程

假设相机坐标系下的点为$(x,y,x)$ ，像素坐标为$(u,v)$，$d=\sqrt{x^2+y^2+z^2}$ 那么它的投影过程为:

1. 将场景点投影在单位球体上，得到：
   $$P_s=\frac{P}{\Vert P\Vert }=\left(\frac{x}{d},\frac{y}{d},\frac{z}{d}\right)$$
2. 将中心偏离$z$轴 $\xi$ 单位，得：
   $$P_{s^{\prime }}=\left(\frac{x}{d},\frac{y}{d},\frac{z}{d}+\xi \right)=\left(\frac{x}{d},\frac{y}{d},\frac{z+d\xi }{d}\right)$$
3. 到平面距离为1，即归一化坐标为：
   $$P_u=\left(\frac{x}{\xi d+z},\frac{y}{\xi d+z},1\right)$$
4. 投影到针孔模型上：
   $$\left[\begin{array}{l}u\\ v\end{array}\right]=\left[\begin{array}{l}{f}_x\frac{x}{\xi d+z}+c_x\\ f_y\frac{y}{\xi d+z}+c_y\end{array}\right]$$

4.2.2 反投影过程

首先通过针孔相机的反投影过程得到：
$$\left[\begin{array}{l}\tilde{u}\\ \tilde{v}\end{array}\right]=\left[\begin{array}{l}\left(u-c_x\right)/f_x\\ \left(v-c_x\right)/f_y\end{array}\right]$$
最后得到的反投影坐标为：
$${\pi }_u^{-1}(\mathbf{u})=\frac{\xi +\sqrt{\left(1-{\xi }^2\right)\left({\tilde{u}}^2+{\tilde{v}}^2\right)}}{{\tilde{u}}^2+{\tilde{v}}^2+1}\left[\begin{array}{l}\tilde{u}\\ \tilde{v}\\ 1\end{array}\right]-\left[\begin{array}{l}0\\ 0\\ \xi \end{array}\right]$$
将其乘以深度就得到了相机坐标系的点。

在鱼眼DSO(Omnidirectional DSO: Direct Sparse Odometry)中，为了补偿透镜缺陷，对原始图像进行了径向切向去畸变，之后才使用该相机模型。所以在这里发现自己对相机模型和畸变模型一直存在混淆，相机模型应该是投影方式的不同，而去畸变是为了矫正相机透镜缺陷带来的问题，两者其实是独立的。

4.3 EUCM (Extended Unified Camera Model)

由于UCM是将三维点先投影在球面上，而为了表征更复杂的投影效果，EUCM在投影时将上面的球面升级为椭球面，增加了一个椭圆参数$\beta$，其他投影折射过程和UCM一致。当$\beta$为1时，EUCM退化为UCM。对于EUCM模型来说，它需要标定六个参数$[fx,fy,cx,cy,\alpha ,\beta ]$，其中前四个是相机的内参，后两个是畸变系数，可以通过使用kalibr工具进行标定。
有了这6个参数，就可以计算图像的坐标了，它的模型如下，其中 $z$ 为光轴：

• $x$: 相机坐标系坐标
• $x_p$: 投影平面坐标系坐标（椭球坐标）
• $q$: 归一化平面坐标系坐标（M平面）

根据上面的坐标、内参和畸变系数可以得到他们之间的关系。
相机坐标到像素坐标：$\mathbf{x}\to \mathbf{q}\to \mathbf{u}$
                  相机坐标$\to$归一化平面坐标$\to$像素坐标

4.3.1 归一化平面坐标

$$\mathbf{q}=\left[\begin{array}{c}x/[\alpha \rho +(1-\alpha )z]\\ y/[\alpha \rho +(1-\alpha )z]\\ 1\end{array}\right]$$
其中$\rho =\sqrt{\beta \left(x^2+y^2\right)+z^2}$：x, y, z 都是相机坐标系下的坐标。相较于普通的针孔模型，它的归一化坐标多了一个系数，$\alpha$和$\beta$都是畸变系数。

4.3.2 像素坐标

有了归一化平面坐标后，就可以使用内参进行投影了：

$$\pi (\mathbf{x})=\mathbf{u}=\left[\begin{array}{cc}{f}_x& 0\\ 0& f_y\end{array}\right]\left[\begin{array}{l}x/[\alpha \rho +(1-\alpha )z]\\ y/[\alpha \rho +(1-\alpha )z]\end{array}\right]+\left[\begin{array}{c}{c}_x\\ c_y\end{array}\right]$$

4.3.3 像素坐标到相机坐标

在实际情况中，从图像中得到特征点，这是他的像素坐标，如何准确的恢复到世界坐标系中也是很重要的，畸变的影响会导致它最后反投影的点的结果不准确。

4.3.3.1 椭圆球面坐标

该坐标可以通过像素坐标进行转换，假设椭球面坐标${\mathbf{x}}_p={\left[\begin{array}{lll}{m}_x& m_y& m_z\end{array}\right]}^T$，那么它的值为：
$$\begin{array}{c}{m}_x=\frac{u-c_x}{f_x}\\ m_y=\frac{v-c_y}{f_y}\\ m_z=\frac{1-\beta {\alpha }^2{r}^2}{\alpha \sqrt{1-(2\alpha -1)\beta r^2}+(1-\alpha )}\end{array}$$

其中 $r^2=m_x^2+m_y^2$，$r^2\le \frac{1}{\beta (2\alpha -1)}$。归一化平面坐标和椭圆球面坐标只有$z$不相同（归一化平面坐标由椭圆球面坐标投影而来）。

4.3.4 相机坐标

这里的恢复就需要用到两帧图像的对应椭球面坐标进行三角化才可以得到相机坐标，椭球面坐标其实就相当于针孔相机去畸变之后的坐标，根据它得到的路标点才是比较准确的。

4.4 Mei模型

Mei模型主要基于在第三部分中由Geyer和Daniilidis提出的投影模型，详细的推导公式再重写一下。

Full projection model

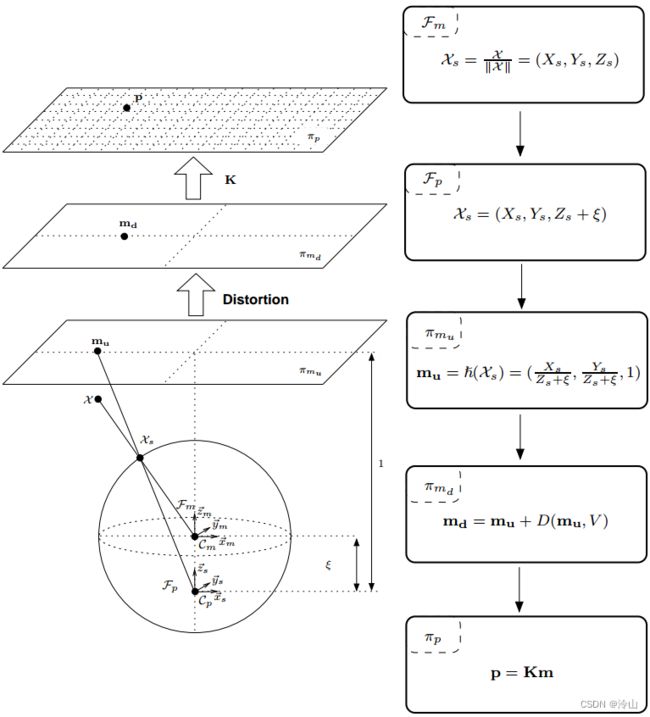
3D点的投影可以通过以下步骤完成：

1. 在 mirror 坐标系上的世界点映射到单位圆上：
   $$(\mathcal{X}{)}_{{\mathcal{F}}_m}\to {\left({\mathcal{X}}_s\right)}_{{\mathcal{F}}_m}=\frac{\mathcal{X}}{\Vert \mathcal{X}\Vert }=\left(X_s,Y_s,Z_s\right)$$

2. 将这些点转换为以 ${\mathcal{C}}_p=(0,0,\xi )$ 为中心的新参考系上：
   $${\left({\mathcal{X}}_s\right)}_{{\mathcal{F}}_m}\to {\left({\mathcal{X}}_s\right)}_{{\mathcal{F}}_p}=\left(X_s,Y_s,Z_s+\xi \right)$$

3. 将它们投影到归一化图像平面上：
   $${\mathbf{m}}_u=\left(\frac{X_s}{Z_s+\xi },\frac{Y_s}{Z_s+\xi },1\right)=\hslash \left({\mathcal{X}}_s\right)$$

4. 添加上径向和切向畸变：
   $${\mathbf{m}}_d={\mathbf{m}}_u+D\left({\mathbf{m}}_u,V\right)$$

5. 最终投影涉及一个广义相机投影矩阵 $\mathbf{K}$(其中 $\gamma$ 为广义焦距，$(u_0,v_0)$ 为主点，$s$ 斜度)：
   $$\mathbf{p}=\mathbf{K}\mathbf{m}=\left[\begin{array}{ccc}\gamma & \gamma s& u_0\\ 0& \gamma r& v_0\\ 0& 0& 1\end{array}\right]\mathbf{m}=k(\mathbf{m})$$

   $\hslash$ 使一个点从 ${\pi }_{m_u}$ 上升(返回)到球面：
   $${\hslash }^{-1}\left({\mathbf{m}}_u\right)=\left[\begin{array}{c}\frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x^2+y^2\right)}}{x^2+y^2+1}x\\ \frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x^2+y^2\right)}}{x^2+y^2+1}y\\ \frac{\xi +\sqrt{1+\left(1-{\xi }^2\right)\left(x^2+y^2\right)}}{x^2+y^2+1}-\xi \end{array}\right]$$

• 未知参数一：从网格参考系到镜像参考系的旋转和平移(外参 $V^1=\left[\begin{array}{llllcc}{q}_{w1}& q_{w2}& q_{w3}& q_{w4}& t_{w1}& t_{w2}\end{array}{t}_{w3}\right]$)
• 未知参数二：在mirror上的反射后点映射在正则化平面上(mirror参数 $V^2=\xi$)
• 未知参数三：使用透镜产生的畸变(畸变参数 $V^3=\left[\begin{array}{llllc}{k}_1& k_2& k_3& k_4& k_5\end{array}\right]$)
• 未知参数四：用广义相机投影矩阵(相机的内参$V^4=\left[\begin{array}{llllc}\alpha & {\gamma }_1& {\gamma }_2& u_0& v_0\end{array}\right]$)，$\gamma$ 包含相机焦距且该参数取决于面镜种类，可在下表中查看，但是在这里可以当成是焦距，而 $u,v$ 表示主点
  总的未知量有18个，通过优化(Levenberg-Marquardt)解得。

关于未知参数三 $V^3$，考虑了两个主要的失真来源：

1. 透镜形状的瑕疵带来的径向失真；
2. 相机安装不当（包括相机光轴和面镜旋转轴没对上）所产生的径向和切向畸变。

畸变函数与针孔模型的相同 $\rho =\sqrt{x^2+y^2}$,
径向畸变：
$$L(\rho )=1+k_1{\rho }^2+k_2{\rho }^4+k_5{\rho }^6$$
切向畸变:
$$dx=\left[\begin{array}{c}2k_{3}xy+k_4({\rho }^2+2x^2)\\ k_3({\rho }^2+2y^2)+2k_{4}xy\end{array}\right]$$

4.5 Scara模型

4.5.1 广角相机模型

校准一个广角相机模型意味着寻找给定的$2D$像素点$p$和从面镜有效视点处传出的$3D$向量$P$之间的关系。一般来说，这个过程需要找到相机的内参和面镜的外参。该广角相机模型将成像系统作为了一个独特的紧凑系统，也就是说，它并不关心在组合相机内使用的是面镜还是鱼眼透镜。

值得注意的是，在此坐标系中，$x$ 和 $u$ 方向向下，$y$ 和 $v$ 方向向右，$z$ 轴透过纸面向外：这与针孔相机模型是相反的。因此在求 $N_Z$ 的时候为负值。

4.5.2 Scara模型假设

该模型基于以下假设：

1. 面镜相机系统是 central 系统，因此，在面镜上存在一个点，每条反射光线都在这个点上相交。这个点被认为是摄像机坐标系 XYZ 的轴原点。
2. 假设相机和面镜的轴被很好的对齐，也就是说，只有很小的旋转偏差被考虑到模型中。（不考虑切向畸变的意思？）
3. 面镜相对于它的轴是旋转对称的。
4. 模型中没有考虑相机的透镜畸变，因为广角相机使用的面镜通常需要大的焦距在面镜上聚焦图像。因此，透镜的失真可以被忽略。如果你使用鱼眼镜头，相机镜头畸变已经被集成在了投影函数$f$里面。

4.5.3 Scara模型

假设假设2是完全符合的，即相机和面镜轴完全的对齐。令$p$为图像的像素点，$(u,v)$是它相对于全向图像中心的像素坐标。设$P$是它对应的从单有效视点发出的三维向量，$(x,y,z)$是它相对于坐标轴原点的坐标。

因为相机和面镜轴假设为完美对齐，因此 $x$ 和 $y$ 分别与 $u$ 和 $v$ 成比例：
$$\left[\begin{array}{l}x\\ y\end{array}\right]=\alpha \cdot \left[\begin{array}{l}u\\ v\end{array}\right],\alpha >0$$

我们想要标定估计的函数是将图像点 $p$ 映射到其对应的 $3D$ 向量 $P$ 的函数。写成：
$$P=\left[\begin{array}{l}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}\alpha \cdot u\\ \alpha \cdot v\\ f(u,v)\end{array}\right]$$

我们可以将$\alpha$包含进函数$f$，因此可以同等的写成：
$$P=\left[\begin{array}{l}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}u\\ v\\ f(u,v)\end{array}\right]$$

事实上，需要注意的是，$P$ 并不是一个 $3D$ 点，而是一个向量，因此前面的简化是被允许的。
而且，因为面镜是旋转对称的，函数 $f(u,v)$ 仅取决于点到图像中心的距离 $\rho =\sqrt{u^2+v^2}$。
因此，我们仍可以将上述的方程简化为：
$$P=\left[\begin{array}{l}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}u\\ v\\ f(\rho )\end{array}\right]$$

在此需要标定的函数只有 $f(\rho )$。该函数是个如下所示的多项式：
$$f(\rho )=a_0+a_1\rho +a_2{\rho }^2+a_3{\rho }^3+a_4{\rho }^4+\dots$$

所以需要估计的参数为：$a_1$, $a_{}$