傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开为傅里叶级数
参考链接:
DR_CAN老师的原视频
0、复习Part2的内容
参考链接:傅里叶级数与傅里叶变换_Part2_周期为2Π的函数展开为傅里叶级数
对于周期为 T = 2 π T = 2\pi T=2π周期函数,即 f ( x ) = f ( x + 2 π ) f\left( x \right) = f\left( {x + 2\pi } \right) f(x)=f(x+2π) ,它的傅里叶级数展开形式如下:
f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n x + ∑ n = 1 ∞ b n sin n x f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} + \sum\limits_{n = 1}^\infty {{b_n}\sin nx} f(x)=2a0+n=1∑∞ancosnx+n=1∑∞bnsinnx
其中,
a 0 = 1 π ∫ − π π f ( x ) d x a n = 1 π ∫ − π π f ( x ) cos n x d x b n = 1 π ∫ − π π f ( x ) sin n x d x \begin{array}{l} {a_0} = \frac{1}{\pi }\int_{ - \pi }^\pi {f\left( x \right)dx} \\\\ {a_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {f\left( x \right)\cos nxdx} \\\\ {b_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {f\left( x \right)\sin nxdx} \end{array} a0=π1∫−ππf(x)dxan=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx
1、周期为2L的函数展开为傅里叶级数
对于, f ( t ) = f ( t + 2 L ) f\left( t \right) = f\left( {t + 2L} \right) f(t)=f(t+2L) ,周期为 T = 2 L T = 2L T=2L的函数

如果想用运用Part2掌握的以 T = 2 π T = 2\pi T=2π为周期的 f ( t ) = f ( t + 2 π ) f\left( t \right) = f\left( {t + 2\pi} \right) f(t)=f(t+2π)的傅里级数展开公式,需要做一个换元。
令 x = π L t ⇒ t = L π x x = \frac{\pi }{L}t \Rightarrow t = \frac{L}{\pi }x x=Lπt⇒t=πLx
| t t t | x x x |
|---|---|
| 2 L 2L 2L | x = π L t = π L ⋅ 2 L = 2 π x = \frac{\pi }{L}t = \frac{\pi }{L} \cdot 2L = 2\pi x=Lπt=Lπ⋅2L=2π |
| 4 L 4L 4L | 4 π 4\pi 4π |
| 0 0 0 | 0 0 0 |
f ( t ) = f ( π L x ) ≜ g ( x ) f\left( t \right) = f\left( {\frac{\pi }{L}x} \right) \triangleq g\left( x \right) f(t)=f(Lπx)≜g(x)
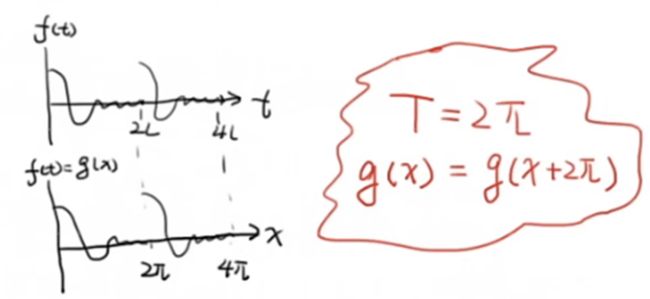
通过换元,我们就把周期为 T = 2 L T = 2L T=2L的函数, f ( t ) = f ( t + 2 L ) f\left( t \right) = f\left( {t + 2L} \right) f(t)=f(t+2L) 变成了周期为 T = 2 π T = 2\pi T=2π的函数 g ( t ) = g ( t + 2 π ) g\left( t \right) =g\left( {t + 2\pi} \right) g(t)=g(t+2π) 。
根据Part2的内容我们知道
g ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n x + ∑ n = 1 ∞ b n sin n x g\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos nx} + \sum\limits_{n = 1}^\infty {{b_n}\sin nx} g(x)=2a0+n=1∑∞ancosnx+n=1∑∞bnsinnx
其中,
a 0 = 1 π ∫ − π π g ( x ) d x a n = 1 π ∫ − π π g ( x ) cos n x d x b n = 1 π ∫ − π π g ( x ) sin n x d x \begin{array}{l} {a_0} = \frac{1}{\pi }\int_{ - \pi }^\pi {g\left( x \right)dx} \\\\ {a_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {g\left( x \right)\cos nxdx} \\\\ {b_n} = \frac{1}{\pi }\int_{ - \pi }^\pi {g\left( x \right)\sin nxdx} \end{array} a0=π1∫−ππg(x)dxan=π1∫−ππg(x)cosnxdxbn=π1∫−ππg(x)sinnxdx
现在要做的,就是把 x = π L t x = \frac{\pi }{L}t x=Lπt带进去
cos n x = cos n π L t , sin n x = sin n π L t \cos nx = \cos \frac{{n\pi }}{L}t,\sin nx = \sin \frac{{n\pi }}{L}t cosnx=cosLnπt,sinnx=sinLnπt
g ( x ) = f ( t ) g\left( x \right) = f\left( t \right) g(x)=f(t)
| x x x | t t t |
|---|---|
| − π -\pi −π | t = L π x = L π ⋅ − π = − L t = \frac{L}{\pi }x = \frac{L}{\pi } \cdot - \pi = - L t=πLx=πL⋅−π=−L |
| π \pi π | L L L |
∫ − π π d x = ∫ − L L d π L t = π L ∫ − L L d t \int_{ - \pi }^\pi {dx} = \int_{ - L}^L {d\frac{\pi }{L}t} = \frac{\pi }{L}\int_{ - L}^L {dt} ∫−ππdx=∫−LLdLπt=Lπ∫−LLdt
1 π ∫ − π π d x = 1 π ⋅ ( π L ∫ − L L d t ) = 1 L ∫ − L L d t \frac{1}{\pi }\int_{ - \pi }^\pi {dx} = \frac{1}{\pi } \cdot \left( {\frac{\pi }{L}\int_{ - L}^L {dt} } \right) = \frac{1}{L}\int_{ - L}^L {dt} π1∫−ππdx=π1⋅(Lπ∫−LLdt)=L1∫−LLdt
讲上述算出的式子带入到 g ( x ) g\left( x\right) g(x)中。
f ( t ) = g ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n π L t + ∑ n = 1 ∞ b n sin n π L t f\left( t \right) = g\left( x\right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos \pmb{\frac{{n\pi }}{L}t}} + \sum\limits_{n = 1}^\infty {{b_n}\sin \pmb{\frac{{n\pi }}{L}t}} f(t)=g(x)=2a0+n=1∑∞ancosLnπtLnπt+n=1∑∞bnsinLnπtLnπt
其中
a 0 = 1 L ∫ − L L f ( t ) d t a n = 1 L ∫ − L L f ( t ) cos n π L t d t b n = 1 L ∫ − L L f ( t ) sin n π L t d t \begin{array}{l} {a_0} =\pmb{ \frac{1}{L}}\int_{ - L}^L {f\left( t \right)dt} \\\\ {a_n} =\pmb{ \frac{1}{L}}\int_{ - L}^L {f\left( t \right)\cos \pmb{\frac{{n\pi }}{L}tdt}} \\\\ {b_n} = \pmb{\frac{1}{L}}\int_{ - L}^L {f\left( t \right)\sin \pmb{\frac{{n\pi }}{L}tdt}} \end{array} a0=L1L1∫−LLf(t)dtan=L1L1∫−LLf(t)cosLnπtdtLnπtdtbn=L1L1∫−LLf(t)sinLnπtdtLnπtdt
在工程当中,由于时间是 t ≥ 0 t \ge 0 t≥0的,所以 t t t是从 0 0 0开始的,假设周期为 T = 2 L T=2L T=2L, ω ≜ π L = 2 π 2 L = 2 π T \omega \triangleq \frac{\pi }{L} = \frac{{2\pi }}{{2L}} = \frac{{2\pi }}{T} ω≜Lπ=2L2π=T2π ,这个 ω \omega ω本质上就是角频率。
再来看积分,因为 − L -L −L ~ L L L是一个周期, 也 0 0 0 ~ 2 L 2L 2L是一个周期,因此 ∫ − L L d t → ∫ 0 2 L d t → ∫ 0 T d t \int_{ - L}^L {dt} \to \int_0^{2L} {dt} \to \int_0^T {dt} ∫−LLdt→∫02Ldt→∫0Tdt,把上述的符号带入到周期为 T = 2 L T = 2L T=2L的傅里叶级数展开公式当中,就可以得到。
f ( t ) = a 0 2 + ∑ n = 1 ∞ a n cos n ω t + ∑ n = 1 ∞ b n sin n ω t f\left( t \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos n\omega t} + \sum\limits_{n = 1}^\infty {{b_n}\sin n\omega t} f(t)=2a0+n=1∑∞ancosnωt+n=1∑∞bnsinnωt
a 0 = 2 T ∫ 0 T f ( t ) d t a n = 2 T ∫ 0 T f ( t ) cos n ω t d t b n = 2 T ∫ 0 T f ( t ) sin n ω t d t \begin{array}{l} {a_0} = \frac{2}{T}\int_0^T {f\left( t \right)dt} \\\\ {a_n} = \frac{2}{T}\int_0^T {f\left( t \right)\cos n\omega tdt} \\\\ {b_n} = \frac{2}{T}\int_0^T {f\left( t \right)\sin n\omega tdt} \end{array} a0=T2∫0Tf(t)dtan=T2∫0Tf(t)cosnωtdtbn=T2∫0Tf(t)sinnωtdt
伏笔: 考虑,当 T → ∞ T \to \infty T→∞时, f ( t ) f\left( t \right) f(t) 不再为周期函数,那时候 f ( t ) f\left( t \right) f(t)该给如何展开呢? 这就是傅里叶变换啦。
2、例子
把下图这个函数,傅里叶展开一下
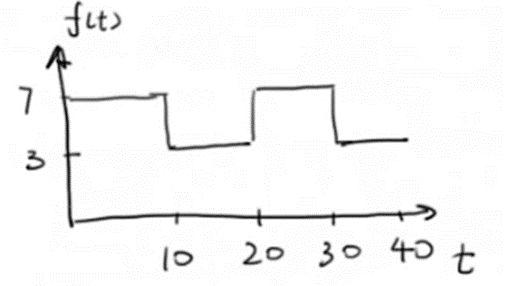
T = 20 , ω = 2 π T = 2 π 20 = 1 10 π T = 20,\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{20}} = \frac{1}{{10}}\pi T=20,ω=T2π=202π=101π
a 0 = 2 T ∫ 0 T f ( t ) d t = 2 T ∫ 0 T 2 7 d t + 2 T ∫ T 2 T 3 d t = 7 + 3 = 10 {a_0} = \frac{2}{T}\int_0^T {f\left( t \right)dt} = \frac{2}{T}\int_0^{\frac{T}{2}} {7dt} + \frac{2}{T}\int_{\frac{T}{2}}^T {3dt} = 7 + 3 = 10 a0=T2∫0Tf(t)dt=T2∫02T7dt+T2∫2TT3dt=7+3=10
a n = 2 T ∫ 0 T f ( t ) cos n ω t d t = 2 T ∫ 0 T 2 7 cos n π 10 t d t + 2 T ∫ T 2 T 3 cos n π 10 d t = 1 10 ⋅ ( 70 n π sin n π 10 t ∣ 0 10 ) + 1 10 ⋅ ( 30 n π sin n π 10 t ∣ 10 20 ) = 1 10 ⋅ ( 0 + 0 ) = 0 \begin{aligned} {a_n} &= \frac{2}{T}\int_0^T {f\left( t \right)\cos n\omega tdt} = \frac{2}{T}\int_0^{\frac{T}{2}} {7\cos \frac{{n\pi }}{{10}}tdt} + \frac{2}{T}\int_{\frac{T}{2}}^T {3\cos \frac{{n\pi }}{{10}}dt} \\ & = \frac{1}{{10}} \cdot \left( {\frac{{70}}{{n\pi }}\sin \frac{{n\pi }}{{10}}t\left| {_0^{10}} \right.} \right) + \frac{1}{{10}} \cdot \left( {\frac{{30}}{{n\pi }}\sin \frac{{n\pi }}{{10}}t\left| {_{10}^{20}} \right.} \right) = \frac{1}{{10}} \cdot \left( {0 + 0} \right) = 0 \end{aligned} an=T2∫0Tf(t)cosnωtdt=T2∫02T7cos10nπtdt+T2∫2TT3cos10nπdt=101⋅(nπ70sin10nπt∣ ∣010)+101⋅(nπ30sin10nπt∣ ∣1020)=101⋅(0+0)=0
b n = 2 T ∫ 0 T f ( t ) sin n ω t d t = 2 T ∫ 0 T 2 7 sin n π 10 t d t + 2 T ∫ T 2 T 3 sin n π 10 d t = 1 10 ⋅ ( − 70 n π cos n π 10 t ∣ 0 10 ) + 1 10 ⋅ ( − 30 n π cos n π 10 t ∣ 10 20 ) = − 7 n π ( cos n π − 1 ) − 3 n π ( cos 2 n π − cos n π ) \begin{aligned} {b_n} &= \frac{2}{T}\int_0^T {f\left( t \right)\sin n\omega tdt} = \frac{2}{T}\int_0^{\frac{T}{2}} {7\sin \frac{{n\pi }}{{10}}tdt} + \frac{2}{T}\int_{\frac{T}{2}}^T {3\sin \frac{{n\pi }}{{10}}dt} \\ &= \frac{1}{{10}} \cdot \left( { - \frac{{70}}{{n\pi }}\cos \frac{{n\pi }}{{10}}t\left| {_0^{10}} \right.} \right) + \frac{1}{{10}} \cdot \left( { - \frac{{30}}{{n\pi }}\cos \frac{{n\pi }}{{10}}t\left| {_{10}^{20}} \right.} \right)\\ & = - \frac{7}{{n\pi }}\left( {\cos n\pi - 1} \right) - \frac{3}{{n\pi }}\left( {\cos 2n\pi - \cos n\pi } \right) \end{aligned} bn=T2∫0Tf(t)sinnωtdt=T2∫02T7sin10nπtdt+T2∫2TT3sin10nπdt=101⋅(−nπ70cos10nπt∣ ∣010)+101⋅(−nπ30cos10nπt∣ ∣1020)=−nπ7(cosnπ−1)−nπ3(cos2nπ−cosnπ)
当 n n n为偶数时, cos n π = cos 2 n π = 1 \cos n\pi = \cos 2n\pi = 1 cosnπ=cos2nπ=1
b n = − 7 n π ( 1 − 1 ) + − 3 n π ( 1 − 1 ) = 0 {b_n} = - \frac{7}{{n\pi }}\left( {1 - 1} \right) + - \frac{3}{{n\pi }}\left( {1 - 1} \right) = 0 bn=−nπ7(1−1)+−nπ3(1−1)=0
当 n n n为奇数时, cos n π = − 1 , cos 2 n π = 1 \cos n\pi = - 1,\cos 2n\pi = 1 cosnπ=−1,cos2nπ=1
b n = − 7 n π ( − 1 − 1 ) − 3 n π [ 1 − ( − 1 ) ] = 8 n π {b_n} = - \frac{7}{{n\pi }}\left( { - 1 - 1} \right) - \frac{3}{{n\pi }}\left[ {1 - \left( { - 1} \right)} \right] = \frac{8}{{n\pi }} bn=−nπ7(−1−1)−nπ3[1−(−1)]=nπ8
所以
f ( t ) = 10 2 + ∑ n = 1 ∞ 0 ⋅ cos π 10 n t + ∑ n = 1 ∞ b n sin π 10 n t = 5 + ∑ n = 1 ∞ 8 n π ⋅ sin n π 10 t , n = 1 , 3 , 5 , 7 , ⋯ \begin{aligned} f\left( t \right) &= \frac{{10}}{2} + \sum\limits_{n = 1}^\infty {0 \cdot \cos \frac{\pi }{{10}}nt} + \sum\limits_{n = 1}^\infty {{b_n}\sin \frac{\pi }{{10}}nt} \\ &= 5 + \sum\limits_{n = 1}^\infty {\frac{8}{{n\pi }} \cdot \sin \frac{{n\pi }}{{10}}} t,n = 1,3,5,7, \cdots \end{aligned} f(t)=210+n=1∑∞0⋅cos10πnt+n=1∑∞bnsin10πnt=5+n=1∑∞nπ8⋅sin10nπt,n=1,3,5,7,⋯
close all; clear all; clc;
dt = 0.1;
t = 0:dt:40;
ft = zeros(length(t),1);
for i=1:length(t)
if (t(i) >= 0 && t(i) <= 10) || (t(i) >= 20 && t(i) <= 30)
ft(i) = 7;
else
ft(i) = 3;
end
end
figure(1);plot(t,ft,'r-','LineWidth',2);grid on;hold on;axis([0,40,0,10]);
FourierSerier0 = 5 * ones(length(t),1);
% n = 1
FourierSerier1 = (8/(1*pi)) * sin((1*pi/10)*t);
% n = 3
FourierSerier3 = (8/(3*pi)) * sin((3*pi/10)*t);
% n = 5
FourierSerier5 = (8/(5*pi)) * sin((5*pi/10)*t);
% n = 7
FourierSerier7 = (8/(7*pi)) * sin((7*pi/10)*t);
% n = 9
FourierSerier9 = (8/(9*pi)) * sin((9*pi/10)*t);
% n = 11
FourierSerier11 = (8/(11*pi)) * sin((11*pi/10)*t);
Fs5 = FourierSerier0 + FourierSerier1 + FourierSerier3 + FourierSerier5;
Fs5 = Fs5';
Fs11 = FourierSerier0 + FourierSerier1 + FourierSerier3 + FourierSerier5 + FourierSerier7 + FourierSerier9 + FourierSerier11;
Fs11 = Fs11';
plot(t,Fs5,'b-','LineWidth',1.5); hold on;
plot(t,Fs11,'k-','LineWidth',2.5);hold on;
legend('f(t)','f(t)傅里叶级数(n取到5)',' f(t)傅里叶级数(n取到11)');
系列学习链接:欢迎大家点赞、收藏、留言讨论。
傅里叶级数与傅里叶变换_Part0_欧拉公式证明+三角函数和差公式证明
傅里叶级数与傅里叶变换_Part1_三角函数系的正交性
傅里叶级数与傅里叶变换_Part2_周期为2Π的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part4_傅里叶级数的复数形式
傅里叶级数与傅里叶变换_Part5_傅里叶级数推导傅里叶变换
傅里叶级数与傅里叶变换_Part6_离散傅里叶变换推导
傅里叶级数与傅里叶变换_Part7_离散傅里叶变换的性质
