【时间序列分析基础系列之二】自回归分布滞后模型

1 分布滞后模型和自回归模型的关系

1.1 分布滞后模型

也就是在计量经济学模型中引入时间维度，通常就是将$X$的滞后经济变量引入模型：
$$Y_t=\alpha +{\beta }_0{X}_t+{\beta }_1{X}_{t-1}+...+{\beta }_s{X}_{t-s}+u_t$$
即$Y$的当期值会受到$X$与$X$的滞后项影响，也就是$X$当期值和过去值的影响，$X$的影响存在长期影响。

1.2 自回归模型

即$Y$的当期值依赖于自身的滞后值，还依赖于其他解释变量
$$Y_t={\alpha }_0+{\alpha }_1{Y}_{t-1}+...+{\alpha }_s{Y}_{t-s}++\beta X_t+u_t$$
自己的理解就是，分布滞后模型中表示X对Y有长期影响，自回归模型表示Y具有长期记忆性。

1.3 动态分布滞后模型（ADL模型）

用ADL$(m,s,p)$表示，其中$m$是自回归阶数，$s$是分布滞后阶数，$p$是外生变量个数。
$$Y_t=\alpha +\sum _{i=1}^m{\alpha }_i{Y}_{t-i}+\sum _{j=1}^p\sum _{i=0}^s{\beta }_{ji}{X}_{jt-i}+u_t$$

2 缓解多重共线性的估计方法

对于分布滞后模型来说，多重共线性问题非常严重，通常采用对各个系数施加先验的约束条件来减少待估计参数的数目，从而缓解多重共线性问题。
最常用的先验约束条件有两种：

1. 假定解释变量滞后阶数为无穷大，且滞后项系数按几何级数递减：
   $$Y_t=\alpha +\beta \lambda X_t+\beta lambd{a}^2{X}_{t-1}+...+u_t$$
2. 假定各滞后项系数变化可以用多项式描述，去进行曲线拟合：
   $$Y_t=\alpha +{\beta }_0{X}_t+{\beta }_1{X}_{t-1}+...+{\beta }_s{X}_{t-s}+u_t$$
   其中，
   $${\beta }_i={\alpha }_o+{\alpha }_{1}i+{\alpha }_2{i}^2+...+{\alpha }_p{i}^p$$

其中p为多项式的阶数，也就是用一个p阶多项式来刻画分布滞后的系数，最大滞后周期m和多项式阶数p可自由选择。

2.1 第一类先验约束条件的解决方法

第一类先验约束条件是假设无限滞后分布加上按照几何级数递减。
$$Y_t=\alpha +\beta \lambda X_t+\beta {\lambda }^2{X}_{t-1}+...+u_t$$
上式仅有三个参数：$\alpha ,\beta 和\lambda$。但是直接估计上式不可行，有两个原因：第一，估计无限多个系数不可行；第二，从回归结果来看，可能$\beta 和\lambda$存在多重解。所以需要用些其他方法求解近似解。

2.1.1 非线性最小二乘法(NLS)

非线性最小二乘法实际上是一种格点搜索法。首先定义$\lambda$的范围（如0-1），指定一个步长（如0.01），然后每次增加一个步长，依次考虑0.01,0.02,……0.99。步长越小，结果精确度越高，当然计算的时间也越长。
建模步骤：

1. 对于$\lambda$的每个值，计算:
   $$Z_t=X_t+\lambda X_{t-1}+{\lambda }^2{X}_{t-2}+...+{\lambda }^p{X}_{t-p}$$

滞后阶数P的选择准则是，P充分大，这时λP充分小，使得X的P阶以后滞后值对Z无显著影响。

2. 然后回归下面的方程：
   $$Y_t=\alpha +\beta Z_t+u_t$$
3. 对$\lambda$的所有取值重复执行上述步骤，选择回归方程产生最高的$R^2$的$\lambda$值，则与此$\lambda$值相对应的$\alpha$和$\beta$的估计值即为该回归所得到的估计值。

2.1.2 科克变换

科克变换就是无限阶几何分布滞后变成自回归模型的形式，具体变换方法如下：

1. 对分布滞后模型两端同取一期滞后：
   $$Y_{t-1}=\alpha +\beta X_{t-1}+\beta \lambda X_{t-2}+\beta {\lambda }^2{X}_{t-3}...+u_{t-1}$$
2. 等式两边同乘$\lambda$，得：
   KaTeX parse error: Undefined control sequence: \lambdaY at position 2: \̲l̲a̲m̲b̲d̲a̲Y̲_{t-1} = \alpha…
3. 用分布滞后元模型减去上式：
   $$\begin{array}{rl}{Y}_t-\lambda Y_{t-1}& =\alpha +\beta X_t+\beta \lambda X_{t-1}+\beta {\lambda }^2{X}_{t-2}+...+u_t\\ & -(\alpha +\beta \lambda X_{t-1}+\beta {\lambda }^2{X}_{t-2}+\beta {\lambda }^3{X}_{t-3}...+u_{t-1})\\ & =\alpha (1-\lambda )+\beta X_t+u_t-\lambda u_{t-1}\end{array}$$
4. 调整一下：
   $$Y_t=\alpha (1-\lambda )+\beta X_t+\lambda Y_{t-1}+u_t-\lambda u_{t-1}$$
   上式中，X的变动对Y的短期影响为β。长期影响为β/(1-λ)，若λ位于0和1之间，则即长期影响大于短期影响。

2.1.2.1 适应预期模型

2.1.2.2 部分调整模型

2.2 第二类先验约束条件的解决方法

但在某些情况下，解释变量的动态影响为一开始小，随时间变大，然后再次衰减。这时各滞后项系数的变化可以用多项式来描述，因此成为阿尔蒙多项式分布滞后。它是强力的曲线拟合工具，其中二次多项式表现为抛物线。

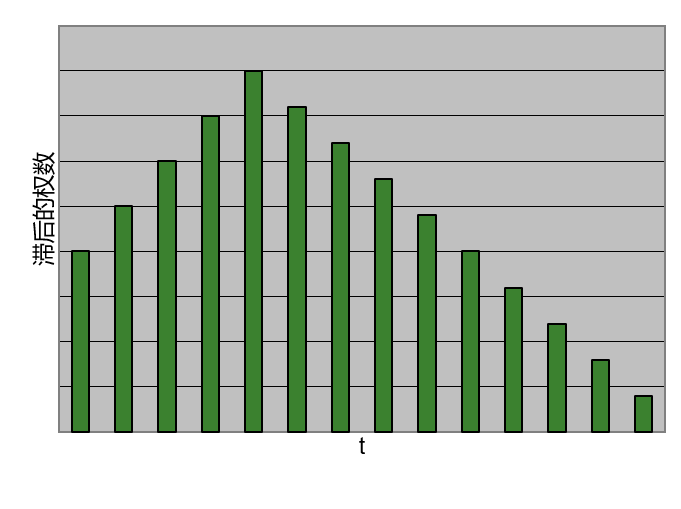
假设分布滞后模型为以下形式：
$$Y_t=\alpha +{\beta }_0{X}_t+{\beta }_1{X}_{t-1}+...+{\beta }_s{X}_{t-s}+u_t$$
假定：
$${\beta }_i={\alpha }_o+{\alpha }_{1}i+{\alpha }_2{i}^2+...+{\alpha }_p{i}^p$$

其中p为多项式的阶数，也就是用一个p阶多项式来刻画分布滞后的系数，最大滞后周期m和多项式阶数p可自由选择。

3 动态分布滞后模型(ADL)

由于动态分布滞后模型通常存在非常严重的多重共线性，为了剔除多重共线性，大佬们想了一个方法，也就是把短期和长期影响进行分离，从而剔除由于滞后项带来的多重共线性。
简而言之，就是用分析长期关系的方法，消除由于滞后项带来的多重共线性
一般的动态分布滞后模型为：
$$Y_t=\alpha +\sum _{i=1}^m{\alpha }_i{Y}_{t-i}+\sum _{j=1}^p\sum _{i=0}^s{\beta }_{ji}{X}_{jt-i}+u_t$$

用ADL$(m,s,p)$表示，其中$m$是自回归阶数，$s$是分布滞后阶数，$p$是外生变量个数。

分析长期影响非常简单，直接对ADL模型等式两边取无条件期望（以ADL(1,1)为例）：
$$Y_t={\alpha }_0+{\alpha }_1{y}_{t-1}+{\beta }_0{x}_t+{\beta }_1{x}_{t-1}+u_t$$
$$E(y_t)=\frac{{\alpha }_0}{1-{\alpha }_1}+\frac{{\beta }_0+{\beta }_1}{1-{\alpha }_1}E(X_t)={\theta }_0+{\theta }_1{x}_t$$
上式称作静态模型，参数称作静态参数或长期参数。长期参数描述变量之间稳定的均衡关系。
动态模型中的参数称作动态参数或短期参数。短期参数描述变量通向均衡状态过程中的非均衡关系。

4 误差修正模型(ECM)

模型推导

ECM模型由 ADL (m, n, p) 模型变换而来。 下面通过ADL (1, 1) 模型推导简单的ECM模型:
$$Y_t={\alpha }_0+{\alpha }_1{y}_{t-1}+{\beta }_0{x}_t+{\beta }_1{x}_{t-1}+u_t,|{\alpha }_1|<1,u_t-IID(0,{\sigma }^2)$$

ut应不存在自相关和异方差。如果不满足，可通过增加xt和 yt的滞后项或加入新的变量从而使ut满足要求。

从上式两侧同时减$y_{t-1}$，在右侧同时加减 ${\beta }_0{x}_{t-1}$得:
$$\Delta Y_t={\alpha }_0+{\beta }_0\Delta x_t+({\alpha }_1-1)y_{t-1}+({\beta }_0+{\beta }_1)x_{t-1}+u_t$$
上式右侧第三、四项合并，
$$\Delta Y_t={\alpha }_0+{\beta }_0\Delta x_t+({\alpha }_1-1)(y_{t-1}-k_1{x}_{t-1})+u_t$$
其中，
$$k_1=\frac{{\beta }_0+{\beta }_1}{1-{\alpha }_1}$$
在上述变换中没有破坏恒等关系，所以不会影响模型对样本数据的解释能力，也不会改变OLS估计量的性质。
进一步变换，可得ECM模型的标准形式：
$$\Delta Y_t={\beta }_0\Delta x_t+({\alpha }_1-1)(y_{t-1}-k_0-k_1{x}_{t-1})+u_t,其中,k_1=\frac{{\beta }_0+{\beta }_1}{1-{\alpha }_1}$$
进一步看看这个ECM模型的式子：
其中，$x_t$和$y_t$长期关系表示为：
$$y_{t-1}=k_0+k_1{x}_{t-1}$$
$x_t$和$y_t$短期关系表示为：
$$\Delta y_t={\beta }_0\Delta x_t+({\alpha }_1-1)(\cdot )$$
前一期的非均衡误差表示为：
$$(y_{t-1}-k_0-k_1{x}_{t-1})$$
误差修正项表示为：
$$({\alpha }_1-1)(y_{t-1}-k_0-k_1{x}_{t-1})$$

若$y_t$平稳，必有 $|{\alpha }_1|<1$，所以非均衡误差项的系数 $({\alpha }_1-1)$ 必为负。说明误差修正项对$\Delta y_t$有一个反向修正作用。

当前一期$y_t$，即$y_{t-1}$相对于均衡点取值过高（低）时，通过误差修正项的反向修正作用，使本期$y_t$减小（增加），$y_t$向均衡位置移动。$({\alpha }_1-1)$表示误差修正项对$\Delta y_t$的调节速度。

---

ECM模型的特点

1. 误差修正模型中既有描述变量长期关系的参数，又有描述变量短期关系的参数；既可研究经济问题的静态（长期）特征又可研究其动态（短期）特征。
2. 误差修正模型中的变量不存在多重共线性问题。
3. 如何估计ECM模型：
   对于平稳变量：
   1）推导法：先建立ADL模型，然后再通过变形推导为ECM模型
   2）直接估计法：把误差修正项的括号打开，对被解释变量为$\Delta y_t$，解释变量为$\Delta x_t$，$\Delta y_{t-1}$，$\Delta x_{t-1}$的模型直接用OLS法估计。

对于非平稳变量，则只有当变量间存在协整关系时，才能得到ECM模型，方法是先估计长期均衡关系，然后把估计的非均衡误差作为误差修正项代入ECM模型，并估计该模型。

3. 对于直接估计ECM模型的方法，在建模过程中允许根据t检验和F检验剔除ECM模型中的差分变量。在ECM模型中剔除差分变量，相当于在原ADL 模型中施加一个约束条件。例如剔除差分变量$\Delta x_t$，相当于在原ADL(1, 1) 模型中施加约束条件，${\beta }_0=0$。
4. 在非均衡误差项中剔除任何水平滞后变量都是危险的，这将影响长期关系的表达。