传教士野人问题 深度优先算法 C++实现

传教士与野人问题

问题的形式化

问题重述

河的左岸有3个传教士3个野人，需要用一条船把所有人都运到河对岸，船每次运输的人数不超过两人，需要保证任何时刻（左岸、右岸、船上）野人数目不超过传教士的数目（传教士数目为0时除外）。求解安全过岸的方案。

变量定义

传教士数量	M
野人数量	C
船的最大承载量	K
左岸	L
右岸	R
船的状态	B

状态表示

用三元组（ML,CL,BL）表示左岸状态
其中0≤ML,BL≤3,BL∈{-1,1} （BL=1表示在左岸，BL=-1表示在右岸）
考虑ML,CL,BL的所有情况共有32种状态，通过约束条件去除其中不合理的状态，共有16种可用状态，构成状态空间。

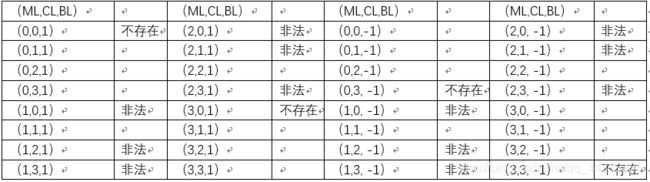
其中初始状态为：（3,3,1）结束状态为（0,0,0）。

动作表示

定义二元组（MB,CB）表示船上的传教士人数和野人人数。根据M和C的取值写出所有可能组合后，根据规则：

• 1.船上有传教士时，野人数目不能超过传教士
• 2.总人数不能超过船的承载量

可以得到所有动作的集合
例如当K=3时
Actions：{（2,0），（0,2），（1,1，），（1,0），（0,1）}

转换模型

由于在状态表示中，我们采用了1和-1来表示船的位置，因此在可以不必在动作中区分向左滑还是向右滑，而在转换模型中通过状态模型中的BL来区分。

目标测试

若当前状态下ML=0且CL=0则达到目标状态。

路径代价

在此例中记每次过河的代价相同都为1。

深度优先搜索

算法逻辑设计

算法的基本思想是通过栈进行递归。
由用户输入传教士和野人数量之后生成初始节点后进入递归函数。

• 在递归函数内首先判断当前节点是否为目标节点，若是目标节点则打印栈中的全部节点作为一条路径，然后跳出本轮递归。
• 其次对当前节点的合法性进行判断，包括人数是否出现负数，传教士是否安全以及是否与栈中的其他节点有重复，若当前节点非法，则跳出本层递归。
• 若以上检验均通过则，对当前节点依次进行八种动作（当K=3时，所有可能的动作共有8种）。每进行完一次操作则以新生成的节点作为当前节点再次进入递归函数。

当最外层递归函数退出时，则将全部节点遍历了一遍，并找出了全部可能的路径。

算法数据结构设计

由于传教士和野人的数量是固定的，因此只需记录一侧传教士与野人的数量即可。定义结构体state用于描述状态节点。结构体包含三个变量，分别记录左侧传教士人数，右侧传教士人数和船的状态。

struct state
{
	int ml;//左侧传教士
	int cl;//左侧野人
	int bl;//bl=1船在左侧;bl=-1船在右侧
};

定义结构体数组，用于递归算法的实现。

struct state statearr[MAX];

定义变量index用作栈顶指针。

int index = 0;//节点标号

定义变量passnum用于记录寻找到的路径数量

int passnum = 0;//路径条数

代码

//传教士与野人问题 深度优先搜索 递归算法
#include 
#include 

#define MAX 100 //k(m+1)^2<=max

//状态节点
struct state
{
	int ml;//左侧传教士
	int cl;//左侧野人
	int bl;//bl=1船在左侧;bl=-1船在右侧
};


struct state statearr[MAX];
int index = 0;//节点标号
int passnum = 0;//路径条数
int m;//传教士人数
int c;//野人人数
int k;//船上的最大人数

clock_t clockstart, clockend;



int handle_DFS(state s)//判断当前节点是否合法
{
	//是否达到目标状态 如果达到目标状态则打印所有路径
	if (s.ml == 0 && s.cl == 0)
	{
		passnum++;
		printf("第%d条路径\n", passnum);
		for (int i = 0; i < index+1; i++)
		{
			printf("(%d,%d,%d)\n", statearr[i].ml, statearr[i].cl, statearr[i].bl);
			
		}
		return 0;
	}
	//人数是否都是正数
	if (s.ml < 0 || s.cl < 0 || s.ml>m || s.cl>c)
		return 0;
	//传教士是否安全
	if ((s.ml != 0 && s.ml < s.cl) || (m - s.ml) != 0 && (m - s.ml) < (c - s.cl))
		return 0;

	//是否回到之前状态
	for (int i = 0; i < index; i++)
	{
		if (s.ml == statearr[i].ml && s.cl == statearr[i].cl && s.bl == statearr[i].bl )
			return 0;
	}

	//此处对应的是K=3 的情况
	//三个传教士过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].ml = statearr[index - 1].ml - statearr[index - 1].bl*3;
	statearr[index].cl = statearr[index - 1].cl;

	handle_DFS(statearr[index]);
	index--;

	//两个传教士和一个野人过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].ml = statearr[index - 1].ml - statearr[index - 1].bl*2;
	statearr[index].cl = statearr[index - 1].cl - statearr[index - 1].bl;

	handle_DFS(statearr[index]);
	index--;

	//两个传教士过河
	index++;
	statearr[index].bl = -1 * statearr[index-1].bl;
	statearr[index].ml = statearr[index-1].ml - statearr[index-1].bl * 2;
	statearr[index].cl = statearr[index - 1].cl;

	handle_DFS(statearr[index]);
	index--;

	//一个传教士和一个野人过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].ml = statearr[index - 1].ml - statearr[index - 1].bl;
	statearr[index].cl = statearr[index - 1].cl - statearr[index - 1].bl;

	handle_DFS(statearr[index]);
	index--;

	//一个传教士过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].ml = statearr[index - 1].ml - statearr[index - 1].bl;
	statearr[index].cl = statearr[index - 1].cl;

	handle_DFS(statearr[index]);
	index--;

	//三个野人过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].cl = statearr[index - 1].cl - statearr[index - 1].bl * 3;
	statearr[index].ml = statearr[index - 1].ml;

	handle_DFS(statearr[index]);
	index--;

	//两个野人过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].cl = statearr[index-1].cl - statearr[index-1].bl * 2;
	statearr[index].ml = statearr[index - 1].ml;

	handle_DFS(statearr[index]);
	index--;


	//一个野人过河
	index++;
	statearr[index].bl = -1 * statearr[index - 1].bl;
	statearr[index].cl = statearr[index - 1].cl - statearr[index - 1].bl;
	statearr[index].ml = statearr[index - 1].ml;

	handle_DFS(statearr[index]);
	index--;

	return 0;
}

int main()
{
	printf("请输入传教士人数：\n");
	scanf_s("%d",&m);
	printf("请输入野人人数：\n");
	scanf_s("%d", &c);
	//printf("请输入船的最大容纳量：\n");
	//scanf("%d", &k);

	statearr[index].ml = m;
	statearr[index].cl = c;
	statearr[index].bl = 1;

	clockstart = clock();
	handle_DFS(statearr[index]);//深度优先算法
	clockend = clock();
	printf("time:%f\n", double(clockend - clockstart));

	printf("加载完毕");
	system("pause");
	return 0;
}

运行结果：

参考博文：

https://blog.csdn.net/qq_36260974/article/details/84404168