深度学习-torch-卷积神经网络

一、基本概念

• 全连接神经网络：每相邻两个线性层之间的神经元都是全连接的神经网络。
  

• 卷积神经网络：保留数据原有特征情况下，对数据进行降维处理的网络模型。
  经典的卷积神经网络有
  1.LeNet
  
  2.AlexNet
  
  3.VGG Net
  

4.GoogleNet


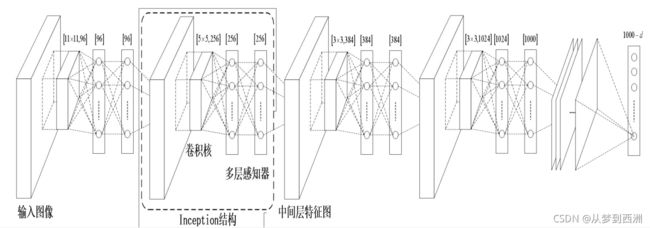
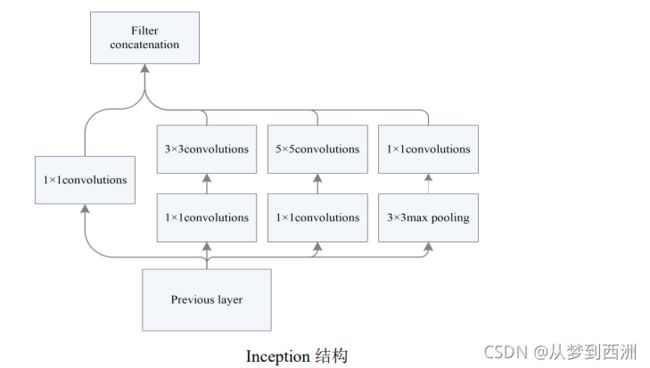
5.ResNet

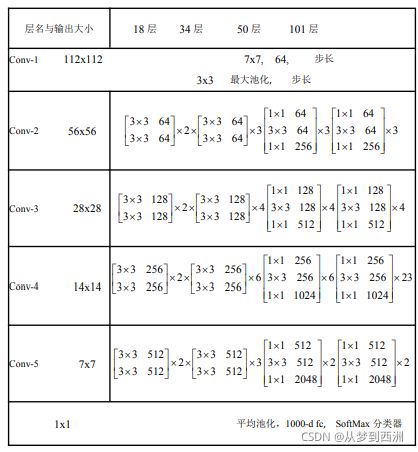
6.MobileNet

二、卷积神经网络的基本组成部分

• 卷积层：用于特征提取
• 池化层：降维、防止过拟合
• 全连接层：输出结果

三、卷积层介绍

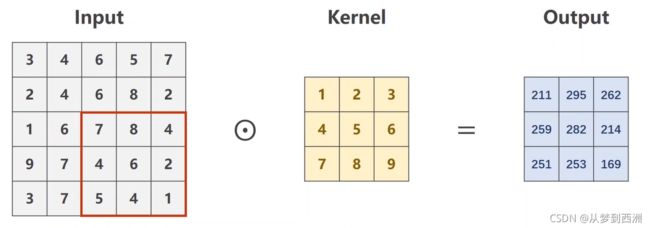
• 假设Input矩阵是单通道矩阵，并且Output矩阵也是单通道的。那么Output矩阵的第一个元素是由Input矩阵中通过卷积核扫描到的第一个矩阵与卷积核进行数乘得到的结果：
  

• 用卷积核依次扫描Input矩阵做数乘，得到Output矩阵。（这里扫描的步长为1）

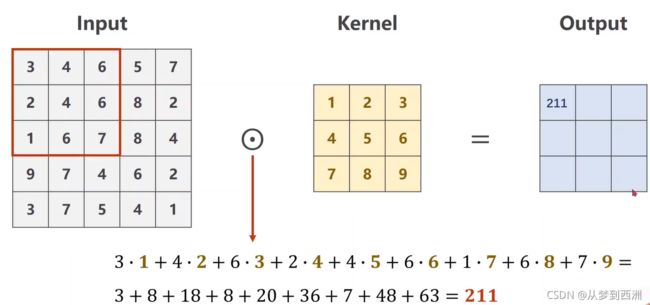
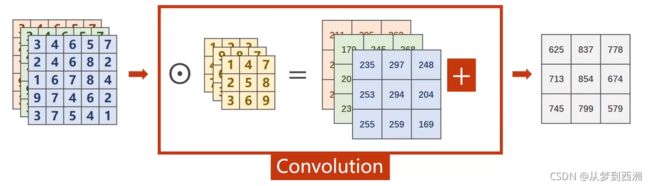
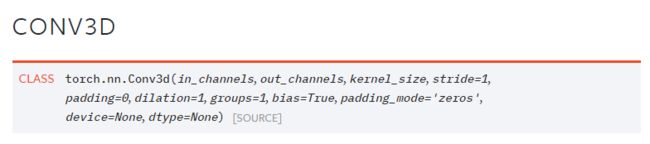
• 对于图片的处理，我们用到的都是二维卷积。n通道的Input矩阵需要用到的卷积核是n维的，用n维卷积核分别对n个通道的Input矩阵扫描做数乘，然后进行矩阵加法，得到单通道的Output矩阵。如果需要的Output矩阵是多通道的，那么需要m个n维卷积核扫描Input矩阵，得到m通道的Output矩阵，因此m的大小决定Output矩阵的通道数。

• 卷积核用于过滤各个图像块，如果某一个图像块和当前的卷积核的卷积结果较大，那么可以认为该图像块和当前卷积核比较接近。
  

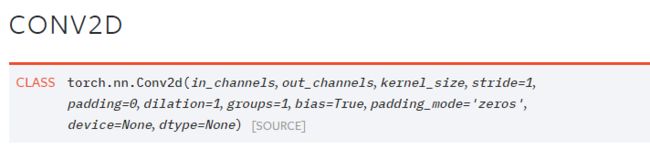
• Conv2D的卷积核形状是二维矩阵，可以是方阵，如3×3；也可以是行列不等的矩阵，如3×5；经过卷积，16通道变33通道。
  
  对于视频的处理，用到的是三维卷积，因图片处理用不到，不做赘述。
  四、卷积层实例介绍

• 以下是将一张图片作为三通道(RGB)Input矩阵，然后用kerner_size=3做卷积的过程：
  

• 3通道的Input矩阵用3维kernel_size=3的卷积核只能得到单通道的Output矩阵。

• 对于n通道的Input矩阵，需要用到n维的卷积核，得到Output矩阵的通道数为1。
  

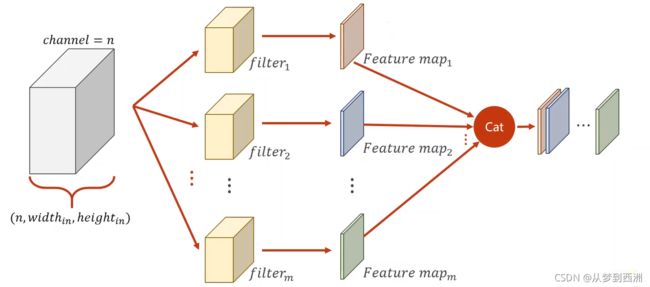
• 如果是想得到多通道矩阵的输出，那么需要多个三维卷积核对三通道的矩阵进行扫描。假设输入通道为n，输出通道为m，那么输入的卷积核的shape应为(m,n,k,k)(k表示kernel_size)，与卷积层的参数注意区分，
  torch.nn.Conv(channel_in,channel_out,kernel_size,padding,stride,bias)
  （卷积核和宽与高可以不等，但一般为方阵，便于计算）
  

• 输出结果为多通道矩阵用到的m个n维的卷积核：
  

• padding：为了保证输入矩阵和输出矩阵的大小保持一致，如果卷积核大小是33，需要进行一圈的填充；如果卷积核大小是55，需要进行两圈的填充。填充圈数=k/5，其中k为卷积核的大小。
  
  五、卷积层代码：

import torch
#初始化一个列表，用于转化成Input矩阵
input=[1, 1, 1,
       1, 1, 1,
       1, 1, 1]

#将输入的列表通过view转化成张量，四个参数分别为（batch,channel,width,height）
input=torch.Tensor(input).view(1,1,3,3)

#定义一个卷积层，参数1,3分别为输入通道，输出通道
#kernel_size表示卷积核是3*3的，也可以用元组(3,3)表示卷积核的大小
#padding=0,表示Input矩阵不做填充，stride=1表示卷积核扫描步长为1
conv_layer=torch.nn.Conv2d(1,3,kernel_size=3,padding=0,stride=1,bias=False)

#定义一个输出通道为3（针对Output矩阵），输入通道为1（针对Input矩阵），大小为3*3的卷积核
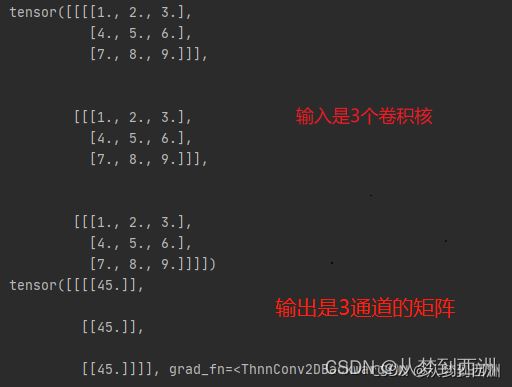
#为了便于计算，一个卷积核与Input矩阵做数乘的结果是45；
kernel=torch.Tensor([1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,]).view(3,1,3,3)
print(kernel)

#conv_layer.weight.data是一个张量
conv_layer.weight.data=kernel.data

#输出为一个张量
output=conv_layer(input)
print(output)

结果输出：

如果要将卷积层改成输入通道为1，输出通道为3，那么Input矩阵应该变成3通道的Input矩阵，采用1个三维的卷积核进行卷积操作。

import torch
#初始化一个列表，用于转化成Input矩阵
input=[1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1,
       1, 1, 1]

#将输入的列表通过view转化成张量，四个参数分别为（batch,channel,width,height）
input=torch.Tensor(input).view(1,3,3,3)

#定义一个卷积层，参数3,1分别为输入通道，输出通道
conv_layer=torch.nn.Conv2d(3,1,kernel_size=3,padding=0,stride=1,bias=False)

#定义一个输出通道为1，输入通道为3，大小为3*3的卷积核
kernel=torch.Tensor([1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,]).view(1,3,3,3)
print(kernel)

#conv_layer.weight.data是一个张量
conv_layer.weight.data=kernel.data

#输出为一个张量
output=conv_layer(input)
print(output)

结果输出：

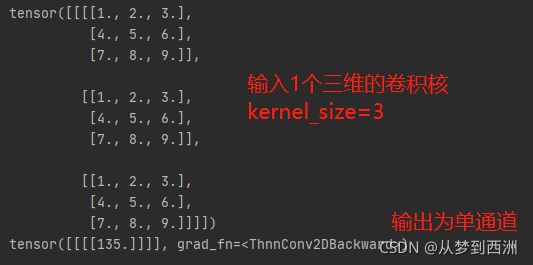
六、池化层介绍
池化层过程又被称为下采样（subsampling），常用池化方法有最大池化和平均池化。

• 最大池化（max-pooling）
  
  参数介绍：
  其实我们常用参数为：kernel_size（区别卷积核），stride，padding
  
  输出shape的W和H计算公式：
  
  假设用一个kernel_size=2×2的maxpooling，默认stride=2，会将Input矩阵划分成一个个2×2大小的矩阵块，取每个矩阵块中的最大元素，然后按照扫描顺序拼接成Output矩阵。

• 平均池化（mean-pooling）
  以AdaptiveAvgpool2D为例：假设Output矩阵的shape是（n,n），那么会将Input矩阵分成n*n个矩阵块，取每个矩阵块的平均值，然后按照矩阵块的排列顺序拼接成Output矩阵。

最大池化和平均池化的代码：

import torch
#输入一个列表，用于转化成Input矩阵
input=[1,2,5,4,
       3,4,6,6,
       2,7,8,10,
       3,4,9,1]

#将输入的列表通过view转化成张量，四个参数分别为（batch,channel,width,height）
input=torch.Tensor(input).view(1,1,4,4)

#定义一个2*2的最大池化层
max_pooling=torch.nn.MaxPool2d(kernel_size=2)
#定义一个平均池化层，输出shape为2*2
mean_pooling=torch.nn.AdaptiveAvgPool2d((2,2))

#输出为一个张量
output_max=max_pooling(input)
output_mean=mean_pooling(input)
print('output_max:\n',output_max)
print('output_mean:\n',output_mean)

结果输出：

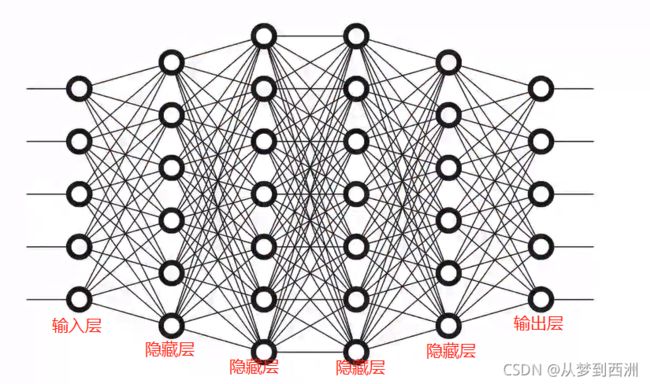
七、全连接层
全连接就是当前层的任意一个神经元与下一层的每一个神经元都进行相连，两层神经元个数不一定相等。全连接层包括Linear，sigmoid，softmax，交叉熵计算等。

• 参考本文第一张全连接神经网络图的隐藏层，假设第l层n个神经元，第l-1层m个神经元。第l层的第k个神经元权重值是由第l-1层与第l层第k个元素相连的m个权重与其对应的第l-1层的m个神经元权重做数乘累加所得。那么第l层n×1大小的神经元权重矩阵则由n×m大小的权重矩阵与第n-1层m×1大小的神经元权重矩阵做矩阵乘法所得。
• 这里举例：torch.nn.Linear(in_features,out_features)，官方解释in_features为每个输入样本的大小，其实我们可以理解为矩阵的列数，那么输出就变成了需要分类的类别数。这里的A.T为形状为： in_features × out_features。
  
  torch.nn.Linear的代码：

import torch
m = torch.nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)
print(output.size())

结果输出：

• sigmoid和softmax应用场景不一样，sigmoid应用于判断事物/场景的准确性，要么是，要么不是，sigmoid值大于50％可以认定为是；softmax应用于多分类问题，会通过torch.nn.Linear()把矩阵的列数减少到类别数，然后用softmax计算每一类别的概率，接着与分类列表计算交叉熵，交叉熵最大则认定这个类别最接近真实值，最后与labels列表比对，相同表示分类正确。交叉熵损失是将softmax输出列(=类别数)与分类列表计算交叉熵累加所得。构造损失函数时，可以把概率计算和交叉熵计算进行合并，用criterion=torch.nn.CrossEntropyLoss()。