分布滞后模型
在涉及时间序列数据的回归分析中,一般由于经济变量自身、决策者心理、技术、制度等方面的原因,解释变量需要经过一段时间才能完全作用于因变量,同时由于经济活动的连续性,因变量的当前变化也往往受到自身过去取值水平的影响,即模型中不仅包含解释变量的当前值,还包含它们的滞后值(过去值),这样的模型称为分布滞后模型(distribution-lag model)。
分布滞后模型可表示为:
y t = α + β 0 x t + β 1 x t − 1 + β 2 x t − 2 + ⋯ + β k x t − k + μ t ( 1 ) {{y}_{t}}=\alpha +{{\beta }_{0}}{{x}_{t}}+{{\beta }_{1}}{{x}_{t-1}}+{{\beta }_{2}}{{x}_{t-2}}+\cdots +{{\beta }_{k}}{{x}_{t-k}}+{{\mu }_{t}} (1) yt=α+β0xt+β1xt−1+β2xt−2+⋯+βkxt−k+μt(1)
或
y t = α + β 0 x t + β 1 x t − 1 + β 2 x t − 2 + ⋯ + μ t ( 2 ) {{y}_{t}}=\alpha +{{\beta }_{0}}{{x}_{t}}+{{\beta }_{1}}{{x}_{t-1}}+{{\beta }_{2}}{{x}_{t-2}}+\cdots +{{\mu }_{t}}(2) yt=α+β0xt+β1xt−1+β2xt−2+⋯+μt(2)
式(1)为有限滞后模型,式(2)为无限滞后模型。其中 k k k为滞后解释变量的滞后期长度。
例:消费滞后。按照一般规律,人们的消费不仅依赖于当期收入,还依赖于前期收入,即人们会分期消费。假定某人收入每年增加1000元,那么这种收入的增加对该消费者的年消费支出会产生什么影响?它也许会在收入增加后的第一年增加400元的消费支出,第二年增加300元,第三年增加200元,把余下的100元作为储蓄。到第三年末此人的消费将增加900元。则消费函数为 y t = α + 0.4 x t + 0.3 x t − 1 + 0.2 x t − 2 + μ t {{y}_{t}}=\alpha +0.4{{x}_{t}}+0.3{{x}_{t-1}}+0.2{{x}_{t-2}}+{{\mu }_{t}} yt=α+0.4xt+0.3xt−1+0.2xt−2+μt。

分布滞后模型的核心思想是多元回归,其一般步骤为:
(1)确定滞后期;
(2)选择适当的方法对模型进行估计;
(3)对所得的回归方程和回归系数进行显著性检验;
(4)分析滞后效应。
第一步:确定滞后期
对于分布滞后模型,首先要确定能够达到的最大滞后期,可以从一个很大的滞后期开始,而不对分布滞后的形状施加任何约束,然后看模型的拟合是否会随滞后期的减小而恶化。也可以通过一些统计检验获取信息,通过多个统计检验综合判断。常用的统计检验有:
(1)相关系数
对于序列 X = { x 1 , x 2 , ⋯ , x n } X=\left\{ {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right\} X={x1,x2,⋯,xn}和 Y = { y 1 , y 2 , ⋯ , y n } Y=\left\{ {{y}_{1}},{{y}_{2}},\cdots ,{{y}_{n}} \right\} Y={y1,y2,⋯,yn},二者在滞后 l l l处的相关系数
R ( l ) = ∑ t = l + 1 n ( x t − x ˉ ) ( y t − l − y ˉ ) ∑ t = l + 1 n ( x t − x ˉ ) 2 ∑ t = 1 n − l ( y t − y ˉ ) 2 R\left( l \right)=\frac{\sum\limits_{t=l+1}^{n}{\left( {{x}_{t}}-\bar{x} \right)\left( {{y}_{t-l}}-\bar{y} \right)}}{\sqrt{\sum\limits_{t=l+1}^{n}{{{\left( {{x}_{t}}-\bar{x} \right)}^{2}}}}\sqrt{\sum\limits_{t=1}^{n-l}{{{\left( {{y}_{t}}-\bar{y} \right)}^{2}}}}} R(l)=t=l+1∑n(xt−xˉ)2t=1∑n−l(yt−yˉ)2t=l+1∑n(xt−xˉ)(yt−l−yˉ)
x ˉ = 1 n − l ∑ t = l + 1 n x t , y ˉ = 1 n − l ∑ t = 1 n − l y t \bar{x}=\frac{1}{n-l}\sum\limits_{t=l+1}^{n}{{{x}_{t}}},\bar{y}=\frac{1}{n-l}\sum\limits_{t=1}^{n-l}{{{y}_{t}}} xˉ=n−l1t=l+1∑nxt,yˉ=n−l1t=1∑n−lyt
其中, l l l的最大取值为 n / 2 {}^{n}/{}_{2} n/2。当 l l l的值从0变化到 n / 2 {}^{n}/{}_{2} n/2时就可以得到多个 R ( l ) R\left( l \right) R(l),令 R ( l ) R\left( l \right) R(l)最大值所对应的滞后为 l max {{l}_{\max }} lmax,如果 R ( l max ) > σ ( σ ∈ [ 0 , 1 ] R\left( {{l}_{\max }} \right)>\sigma (\sigma \in \left[ 0,1 \right] R(lmax)>σ(σ∈[0,1]为用户定义的阈值),那么就说时间序列 X , Y X,Y X,Y具有滞后相关性。

由上图可知,当l=6时,R(l)最大,即居民蛋消费价格指数和棉花产值相关系数最大为0.77,若用户指定的阈值 σ > 0.5 \sigma>0.5 σ>0.5 ,则认为居民蛋消费价格指数和棉花产值具有滞后相关性,且棉花产值滞后于居民蛋消费价格指数的量为6。
(2)调整的判定系数 R ˉ 2 {{\bar{R}}^{2}} Rˉ2
依次添加滞后项,直到 R 2 {{R}^{2}} R2取得极大值,对应的滞后期为最优
R ˉ 2 = 1 − ( 1 − R 2 ) n − 1 n − k − 1 , R 2 = E S S T S S = 1 − R S S T S S {{\bar{R}}^{2}}=1-\left( 1-{{R}^{2}} \right)\frac{n-1}{n-k-1},{{R}^{2}}=\frac{ESS}{TSS}=1-\frac{RSS}{TSS} Rˉ2=1−(1−R2)n−k−1n−1,R2=TSSESS=1−TSSRSS
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 , E S S = ∑ i = 1 n ( y ^ − y ˉ ) 2 , T S S = ∑ i = 1 n ( y − y ˉ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}},ESS=\sum\limits_{i=1}^{n}{{{\left( \hat{y}-\bar{y} \right)}^{2}}},TSS=\sum\limits_{i=1}^{n}{{{\left( y-\bar{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2,ESS=i=1∑n(y^−yˉ)2,TSS=i=1∑n(y−yˉ)2分别为残差平方和、回归平方和、总平方和, n n n为数据数量, k k k为变量个数。
(3)施瓦茨( S C SC SC)准则
依次添加滞后项,直到 S C SC SC达到极小值,对应的滞后期为最优
S C = ln ( R S S n ) + k + 1 n ln n SC=\ln \left( \frac{RSS}{n} \right)+\frac{k+1}{n}\ln n SC=ln(nRSS)+nk+1lnn
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2为残差平方和, n n n为数据数量, k k k为变量个数。
(4)赤池( A I C AIC AIC)准则
依次添加滞后项,直到 A I C AIC AIC达到极小值,对应的滞后期为最优
A I C = ln ( R S S n ) + 2 ( k + 1 ) n AIC=\ln \left( \frac{RSS}{n} \right)+\frac{2\left( k+1 \right)}{n} AIC=ln(nRSS)+n2(k+1)
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2为残差平方和, n n n为数据数量, k k k为变量个数。
例如,有某产品1990年-2008年的库存和销售额数据。

依次添加滞后项,即当期时 Y t = α + β 0 X t {{Y}_{t}}=\alpha +{{\beta }_{0}}{{X}_{t}} Yt=α+β0Xt;添加滞后一期项时, Y t = α + β 0 X t + β 1 X t − 1 + β 2 x t − 2 + ⋯ + β k x t − k + μ t ( 1 ) {{Y}_{t}}=\alpha +{{\beta }_{0}}{{X}_{t}}+{{\beta }_{1}}{{X}_{t-1}}+{{\beta }_{2}}{{x}_{t-2}}+\cdots +{{\beta }_{k}}{{x}_{t-k}}+{{\mu }_{t}} (1) Yt=α+β0Xt+β1Xt−1+β2xt−2+⋯+βkxt−k+μt(1);添加滞后二期项时, Y t = α + β 0 X t + β 1 X t − 1 + β 2 X t − 2 {{Y}_{t}}=\alpha +{{\beta }_{0}}{{X}_{t}}+{{\beta }_{1}}{{X}_{t-1}}+{{\beta }_{2}}{{X}_{t-2}} Yt=α+β0Xt+β1Xt−1+β2Xt−2…依次对各模型进行最小二乘法(OLS)估计,得到判定系数 R ˉ 2 {{\bar{R}}^{2}} Rˉ2、 S C SC SC、 A I C AIC AIC,根据 S C SC SC、 A I C AIC AIC最小,判定系数 R ˉ 2 {{\bar{R}}^{2}} Rˉ2最大,最优滞后期应为2。

第二步:模型估计
分布滞后模型估计不能直接使用最小二乘法(OLS)估计,会遇到多重共线性、损失自由度、滞后长度难以确定等问题。所以实践中很少用OLS方法直接估计分布滞后模型,一般使用限定诸 β \beta β遵从某种先验变化的模式或理论模式。对于有限分布滞后模型,常用的修正估计方法有经验加权法、阿尔蒙多项式法(Almon)等;对于无限分布滞后模型,主要通过适当的模型变换转化为自回归模型进行估计,代表性的方法有考伊克法(Koyck)等。下面介绍有限分布滞后模型的两种估计方法。
(1)经验加权法
根据实际经济问题的特点及经验判断,对滞后变量赋予一定的权数,利用这些权数构成各滞后变量的线性组合,以形成新的变量,再应用最小二乘法进行估计。基本思路是设法减少模型中被估计的参数个数,模型中参数的个数主要由解释变量的个数来决定,要减少模型中被估计的参数个数,就要对解释变量进行归并,并通过解释变量的归并,消除或削弱多重共线性问题。该方法的优点是简单易行、少损失自由度、避免多重共线性。缺点是权数设置主观随意性大。通常的做法是依据先验信息,多选几组权数进行估计模型,最后选择能通过统计和计量经济检验的模型。根据滞后结构特点,常使用的权数类型有:
- 递减滞后结构
例如,消费函数中近期收入对消费的影响较大,而远期收入的影响将越来越小;如果设滞后期为2,各期权数取成 1 / 2 , 1 / 4 , 1 / 6 {1}/{2}\;,{1}/{4}\;,{1}/{6}\; 1/2,1/4,1/6,
则组合成新的解释变量: w t = 1 2 x t + 1 4 x t − 1 + 1 6 x t − 2 {{w}_{t}}=\frac{1}{2}{{x}_{t}}+\frac{1}{4}{{x}_{t-1}}+\frac{1}{6}{{x}_{t-2}} wt=21xt+41xt−1+61xt−2
估计模型(此时模型已无多重共线性): y t = α + β w t + ε t {{y}_{t}}=\alpha +\beta {{w}_{t}}+{{\varepsilon }_{t}} yt=α+βwt+εt
用最小二乘法得到 α , β \alpha ,\beta α,β的估计值,将 w t {{w}_{t}} wt带入原模型得, β ^ 0 = β ^ 2 , β ^ 1 = β ^ 4 , β ^ 2 = β ^ 6 {{\hat{\beta }}_{0}}=\frac{{\hat{\beta }}}{2},{{\hat{\beta }}_{1}}=\frac{{\hat{\beta }}}{4},{{\hat{\beta }}_{2}}=\frac{{\hat{\beta }}}{6} β^0=2β^,β^1=4β^,β^2=6β^ - 不变滞后结构
设滞后期为2,各期权数为 1 / 3 {1}/{3}\; 1/3,则 w t = 1 3 ( x t + x t − 1 + x t − 2 ) {{w}_{t}}=\frac{1}{3}\left( {{x}_{t}}+{{x}_{t-1}}+{{x}_{t-2}} \right) wt=31(xt+xt−1+xt−2)
同理得到原模型各参数的估计值为: β ^ i = β ^ 3 {{\hat{\beta }}_{i}}=\frac{{\hat{\beta }}}{3} β^i=3β^ - A型滞后结构
例如,历年投资对产出的影响一般为A型滞后结构,设滞后期为4,各期权数为 1 / 6 , 1 / 4 , 1 / 2 , 1 / 4 , 1 / 6 {1}/{6}\;,{1}/{4}\;,{1}/{2}\;,{1}/{4}\;,{1}/{6}\; 1/6,1/4,1/2,1/4,1/6,则 w t = 1 6 x t + 1 4 x t − 1 + 1 2 x t − 2 + 1 4 x t − 3 + 1 6 x t − 4 {{w}_{t}}=\frac{1}{6}{{x}_{t}}+\frac{1}{4}{{x}_{t-1}}+\frac{1}{2}{{x}_{t-2}}+\frac{1}{4}{{x}_{t-3}}+\frac{1}{6}{{x}_{t-4}} wt=61xt+41xt−1+21xt−2+41xt−3+61xt−4
同理得到原模型各参数的估计值 β ^ 0 = β ^ 6 , β ^ 1 = β ^ 4 , β ^ 2 = β ^ 2 , β ^ 3 = β ^ 4 , β ^ 4 = β ^ 6 {{\hat{\beta }}_{0}}=\frac{{\hat{\beta }}}{6},{{\hat{\beta }}_{1}}=\frac{{\hat{\beta }}}{4},{{\hat{\beta }}_{2}}=\frac{{\hat{\beta }}}{2},{{\hat{\beta }}_{3}}=\frac{{\hat{\beta }}}{4},{{\hat{\beta }}_{4}}=\frac{{\hat{\beta }}}{6} β^0=6β^,β^1=4β^,β^2=2β^,β^3=4β^,β^4=6β^

(2)阿尔蒙(Almon)多项式法
为了消除多重共线性的影响,阿尔蒙于1965年提出利用有限多项式来减少待估计参数的个数,以消除多重共线性及参数估计中的自由度损失。现实生活中,解释变量系数随滞后期的变化轨迹并不完全遵从几何级数衰减的假定,其变化形式多种多样。

对于有限分布滞后模型
y t = α + β 0 x t + β 1 x t − 1 + β 2 x t − 2 + ⋯ + β k x t − k + μ t {{y}_{t}}=\alpha +{{\beta }_{0}}{{x}_{t}}+{{\beta }_{1}}{{x}_{t-1}}+{{\beta }_{2}}{{x}_{t-2}}+\cdots +{{\beta }_{k}}{{x}_{t-k}}+{{\mu }_{t}} yt=α+β0xt+β1xt−1+β2xt−2+⋯+βkxt−k+μt
可改写为
y t = α + ∑ i = 0 k β i x t − i + μ t {{y}_{t}}=\alpha +\sum\limits_{i=0}^{k}{{{\beta }_{i}}{{x}_{t-i}}}+{{\mu }_{t}} yt=α+i=0∑kβixt−i+μt
其中 β i = a 0 + a 1 i + a 2 i 2 + a 3 i 3 + ⋯ + a m i m {{\beta }_{i}}={{a}_{0}}+{{a}_{1}}i+{{a}_{2}}{{i}^{2}}+{{a}_{3}}{{i}^{3}}+\cdots +{{a}_{m}}{{i}^{m}} βi=a0+a1i+a2i2+a3i3+⋯+amim,一般多项式次数 m m m取2或者3,很少超过4;且多项式的次数 m m m小于最大滞后期 k k k。即参数 β i {{\beta }_{i}} βi可近似的用一个关于滞后期 i i i的低阶多项式表示,进而减少模型中的参数。取 m = 2 m=2 m=2为例进一步说明阿尔蒙方法,有阿尔蒙多项分布滞后模型

其中, z 0 t = ∑ i = 0 k x t − i , z 1 t = ∑ i = 0 k i x t − i , z 2 t = ∑ i = 0 k i 2 x t − i {{z}_{0t}}=\sum\limits_{i=0}^{k}{{{x}_{t-i}}},{{z}_{1t}}=\sum\limits_{i=0}^{k}{i{{x}_{t-i}}},{{z}_{2t}}=\sum\limits_{i=0}^{k}{{{i}^{2}}{{x}_{t-i}}} z0t=i=0∑kxt−i,z1t=i=0∑kixt−i,z2t=i=0∑ki2xt−i。如果随机误差项 μ \mu μ满足经典线性回归的假定,该模型仍可采用最小二乘法估计,且 α \alpha α和 a i {{a}_{i}} ai的估计值将具有全部的优良统计性质。估计出诸 a a a,进而估计出原始的 β \beta β系数

阿尔蒙多项式的应用示例。
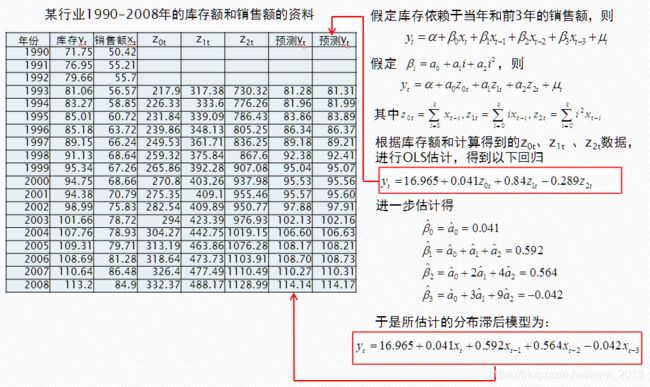
阿尔蒙方法的优点:在阿尔蒙模型中,解释变量不再是x,而是x的线性组合,多重线性可以相对减弱;在使用阿尔蒙方法时,不必担心因滞后变量出现可能产生的估计问题(非随机解释变量和序列相关问题),它依然可以用最小二乘法进行估计;可以拟合一个足够低次的多项式,使估计系数的个数要比原先的系数的个数少很多。
阿尔蒙方法的缺点:(a)滞后期的最大长度和多项式的次数是一种主观判断。若选择了过小的长度将导致“漏掉有关变量”的偏倚,这时系数虽然可以用OLS估计,但系数的方差不那么有效;(b)z变量的个数(m+1) 与m有关,一旦确定了滞后期k和多项式次数m就可以构造出诸z。然而z变量是x变量的线性组合,虽然多重共线问题可以减轻,但并不能消除。因此,在确定选择多项式的次数时,必须先肯定多重共线性的问题可以用前面给的技术方法进行处理。
第三步:模型检验与评估
- 回归方程的显著性检验
统计量: F = E S S / k R S S / ( n − k − 1 ) ∼ F ( k , n − k − 1 ) F=\frac{ESS/k}{RSS/\left( n-k-1 \right)}\sim F\left( k,n-k-1 \right) F=RSS/(n−k−1)ESS/k∼F(k,n−k−1)
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 , E S S = ∑ i = 1 n ( y ^ − y ˉ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}},ESS=\sum\limits_{i=1}^{n}{{{\left( \hat{y}-\bar{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2,ESS=i=1∑n(y^−yˉ)2分别为残差平方和、回归平方和, n n n为数据数量, k k k为变量个数。若 F > F α F>{{F}_{\alpha }} F>Fα或 p < α p<\alpha p<α,则回归方程显著。
- 回归系数的显著性检验
统计量: t i = β ^ i / l i i R S S / ( n − k − 1 ) ∼ t ( n − k − 1 ) {{t}_{i}}=\frac{{{{\hat{\beta }}}_{i}}/\sqrt{{{l}^{ii}}}}{\sqrt{RSS/\left( n-k-1 \right)}}\sim t\left( n-k-1 \right) ti=RSS/(n−k−1)β^i/lii∼t(n−k−1)
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2为残差平方和, n n n为数据数量, k k k为变量个数, l i i {{l}^{ii}} lii为 L − 1 {{L}^{-1}} L−1的第 i i i个对角元素,而 L − 1 = X ~ ′ X ~ {{L}^{-1}}={\tilde{X}}'\tilde{X} L−1=X~′X~, X ~ \tilde{X} X~是中心化的数据阵。若 t > t α t>{{t}_{\alpha }} t>tα或 p < α p<\alpha p<α,则回归系数显著。

- 回归直线对观测值的拟合程度
拟合优度 R 2 {{R}^{2}} R2: R 2 = E S S T S S = 1 − R S S T S S {{R}^{2}}=\frac{ESS}{TSS}=1-\frac{RSS}{TSS} R2=TSSESS=1−TSSRSS
调整的判定系数 R ˉ 2 {{\bar{R}}^{2}} Rˉ2: R ˉ 2 = 1 − ( 1 − R 2 ) n − 1 n − k − 1 {{\bar{R}}^{2}}=1-\left( 1-{{R}^{2}} \right)\frac{n-1}{n-k-1} Rˉ2=1−(1−R2)n−k−1n−1
其中 R S S = ∑ i = 1 n ( y − y ^ ) 2 , E S S = ∑ i = 1 n ( y ^ − y ˉ ) 2 , T S S = ∑ i = 1 n ( y − y ˉ ) 2 RSS=\sum\limits_{i=1}^{n}{{{\left( y-\hat{y} \right)}^{2}}},ESS=\sum\limits_{i=1}^{n}{{{\left( \hat{y}-\bar{y} \right)}^{2}}},TSS=\sum\limits_{i=1}^{n}{{{\left( y-\bar{y} \right)}^{2}}} RSS=i=1∑n(y−y^)2,ESS=i=1∑n(y^−yˉ)2,TSS=i=1∑n(y−yˉ)2分别为残差平方和、回归平方和、总平方和, n n n为数据数量, k k k为变量个数。 R 2 {{R}^{2}} R2和 R ˉ 2 {{\bar{R}}^{2}} Rˉ2越接近于1,说明回归直线对观测值的拟合程度越好;反之,越接近于零说明回归直线对观测值的拟合程度越差。
第四步:滞后效应分析
分布滞后变量模型的各系数体现了解释变量的当期值和各期滞后值对被解释变量的不同影响程度。
- 滞后效应的乘数分析
对于分布滞后模型 y t = α + β 0 x t + β 1 x t − 1 + β 2 x t − 2 + ⋯ + β k x t − k + μ t {{y}_{t}}=\alpha +{{\beta }_{0}}{{x}_{t}}+{{\beta }_{1}}{{x}_{t-1}}+{{\beta }_{2}}{{x}_{t-2}}+\cdots +{{\beta }_{k}}{{x}_{t-k}}+{{\mu }_{t}} yt=α+β0xt+β1xt−1+β2xt−2+⋯+βkxt−k+μt
β 0 {{\beta }_{0}} β0:短期乘数,表示解释变量变化一个单位对同期被解释变量所产生的影响,即短期影响;
β i ( i > 0 ) {{\beta }_{i}}(i>0) βi(i>0):延期乘数或动态乘数,反映解释变量在各滞后时期的单位变化对 y t {{y}_{t}} yt产生的影响,即滞后影响。
∑ i = 0 s β i \sum\limits_{i=0}^{s}{{{\beta }_{i}}} i=0∑sβi:为(s期)中期乘数,反映了解释变量对 y t {{y}_{t}} yt的s期累计影响;
∑ i = 0 ∞ β i \sum\limits_{i=0}^{\infty }{{{\beta }_{i}}} i=0∑∞βi:为长期乘数,表示 x t {{x}_{t}} xt变动一单位对 y t {{y}_{t}} yt产生的累计总影响。
利用乘数可以分析解释变量对解释变量的滞后影响过程。
例如, y ^ t = α ^ + 0.4 x t + 0.3 x t − 1 + 0.2 x t − 2 {{\hat{y}}_{t}}=\hat{\alpha }+0.4{{x}_{t}}+0.3{{x}_{t-1}}+0.2{{x}_{t-2}} y^t=α^+0.4xt+0.3xt−1+0.2xt−2,则短期乘数为0.4,延期乘数为0.3/0.2,长期乘数为0.9。即当收入增加1元时,消费者将在本期增加0.4元的消费,下一期增加0.3元,再下期增加0.2元,增加1元收入对消费的长期作用为0.9元。 - 滞后效应的速度分析
乘数效用比: D s = s = ∑ i = 0 s β i ∑ i = 0 ∞ β i {{D}_{s}}=\frac{s}{}\text{=}\frac{\sum\limits_{i=0}^{s}{{{\beta }_{i}}}}{\sum\limits_{i=0}^{\infty }{{{\beta }_{i}}}} Ds=s=i=0∑∞βii=0∑sβi
D s {{D}_{s}} Ds为截止到第 s s s期为止的乘数效应比,它反映了 x t {{x}_{t}} xt的变动在经历 s s s期后,对 y t {{y}_{t}} yt的影响所达到的程度,使 D s {{D}_{s}} Ds达到某个百分比(如90%)的 s s s值越小,则作用时间越快,滞后时间越短。
平均滞后时间: M L T = ∑ i = 0 ∞ i β i ∑ i = 0 ∞ β i MLT\text{=}\frac{\sum\limits_{i=0}^{\infty }{i{{\beta }_{i}}}}{\sum\limits_{i=0}^{\infty }{{{\beta }_{i}}}} MLT=i=0∑∞βii=0∑∞iβi
称 M L T MLT MLT为平均滞后时间(或平均滞后),实际上是以各期延期乘数为权数的、各滞后期的加权平均数,反映了滞后期的平均长度,其值越小,则平均滞后期越短,表明 y y y对 x x x变化的反映速度越快。

ps:初衷是通过撰写博文记录自己所学所用,实现知识的梳理与积累;将其分享,希望能够帮到面临同样困惑的小伙伴儿。如发现博文中存在问题,欢迎随时交流~~