图像处理入门系列--使用numpy实现OTSU大津法及其改进
大家好,我是CuddleSabe,目前大四在读,深圳准入职算法工程师,研究主要方向为多模态(VQA、ImageCaptioning等),欢迎各位佬来讨论!
我最近在有序地计划整理CV入门实战系列及NLP入门实战系列。在这两个专栏中,我将会带领大家一步步进行经典网络算法的实现,欢迎各位读者(da lao)订阅
使用numpy实现OTSU大津法及其改进
- OTSU大津法
-
- 一、将输入BGR图像转换为GRAY图像
- 二、计算 前/后 景像素比例及其灰度平均值
- 三、计算类间方差并取得最优阈值
- 四、二值化
- 五、我是如何改进的
- **正确答案应该是这样**
- 六、OTSU大津法原理及公式推导
- 七、完整代码
- 八、效果演示
OTSU大津法
OTSU算法是由日本学者OTSU于1979年提出的一种对图像进行二值化的高效算法。
其可分为个步骤:
- 设定初始阈值并将图像转为灰度图像;
- 计算 前/后 景的像素所占比例w0,w1;
- 计算 前/后 景的像素的灰度平均值gray_level0 , gray_level1;
- 计算在不同阈值情况下单类间方差var;
- 使var最大的阈值即为最优阈值best_threshold;
- 二值化;
一、将输入BGR图像转换为GRAY图像
注意,这里如果采用for循环,则运算会慢几十到几百倍,因此这里我们使用矩阵索引的方式来进行运算。(这是因为python为解释型语言,在for每次执行的时候都要进行解释,而numpy则是基于c/c++开发,本质相当于python调用c代码,运行速度杠杠的!)
# Convert BGR to GRAY
@staticmethod
def BGR2GRAY(img):
gray_img = 0.2126 * img[:, :, 0] + 0.7152 * img[:, :, 1] + 0.0722 * img[:, :, 2]
return np.array(gray_img).astype(np.uint8)
这里采用C = 0.2126 * B + 0.7152 * G + 0.0722 * R 公式,效果比普通的求三个通道的平均值要好的多!
二、计算 前/后 景像素比例及其灰度平均值
#BGR转GRAY图像
gray = 0.2126 * img[:, :, 0] + 0.7152 * img[:, :, 1] + 0.0722 * img[:, :, 2]
#将图像在长款上各缩短到1/4,以加快查找阈值
gray_img = gray[::4, ::4]
gray_img = np.array(gray_img).astype(np.uint8)
gray_level0 = np.zeros(256, dtype=np.float)
gray_level1 = np.zeros(256, dtype=np.float)
w0 = np.zeros(256, dtype=np.float)
w1 = np.zeros(256, dtype=np.float)
threshold = np.arange(256).astype(np.uint8)
y_size, x_size = np.shape(gray_img)
#为了更进一步加快大津法,range在最小值和最大值中间,且步长为2
for i in range(gray_img.min(), gray_img.max()):
#计算 前/后 景的像素所占比例
w0[i] = np.shape(gray_img[gray_img > threshold[i]])[0] / (y_size*x_size)
#计算 前/后 景的像素的平均值
gray_level0[i] = np.mean(gray_img[gray_img > threshold[i]])
gray_level1[i] = np.mean(gray_img[gray_img <= threshold[i]])
w1[:] = 1 - w0[:]
三、计算类间方差并取得最优阈值
#计算在不同阈值情况下的 类间方差
var = np.array(w0[:]*w1[:]*(gray_level0[:]-gray_level1[:])**2).astype(np.uint8)
#最优的阈值对应的是最大的 类间方差
best_threshold = threshold[np.argmax(var)]
四、二值化
#通过最优阈值来二值化
gray[gray<best_threshold] = 0
gray[gray>=best_threshold] = 255
五、我是如何改进的
我在编写时,经历了以下几个阶段:
| 阶段 | 遇到的问题 | 解决方案 | 理论提速多少倍 |
|---|---|---|---|
| 一 | 使用for循环导致速度过慢 | 使用Numpy的索引切片运算来代替for循环 | 23333 |
| 二 | 图片过大导致运算变慢 | 将图像在长款上各缩短到1/4,以加快查找阈值 | 提速 4*4 =16 倍 |
| 三 | 同上 | 为了更进一步加快大津法,range在最小值和最大值中间,且步长为2 | 再次提升两倍 |
| (在二值化的时候,很多人会容易写成下面两种) |
一、
for pic in gray:
if pic < best_threshold:
pic = 0
else:
pic = 255
二、 for pic in gray:
pic = 0 if pic < best_threshold else 255
(这样的确是大多数人第一时间容易写出的代码233,但是这是python不是c语言,这样会造成运算时间的极度加长,因为python是解释型语言,在图像处理时应该少用for循环)
正确答案应该是这样
#通过最优阈值来二值化
gray[gray<best_threshold] = 0
gray[gray>=best_threshold] = 255
灵活利用好numpy自身的用法,这可比for快了几十倍!
六、OTSU大津法原理及公式推导
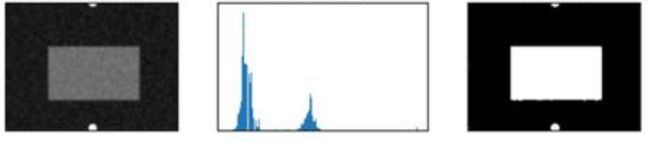
| 如图,左图是一个前景和背景分开很清楚的图,前景为灰色布条,背景为黑色桌布。其灰度直方图为中图,可见其为双峰一谷型,其中每个峰都对应了 前/后 景的灰度。 |
|---|
| 1.我们这里先假设一个阈值 T T T,那么我们将像素是灰度小于 T T T的概率定义为 W 0 W0 W0,反之则为 W 1 W1 W1(一律采用频率来代替概率)。 |
| 2.求出灰度小于 T T T的像素的均值 g r a y _ l e v e l 0 gray\_level0 gray_level0,反之为 g r a y _ l e v e l 1 gray\_level1 gray_level1.全图均值为 t o t a l _ g r a y total\_gray total_gray |
| 3.我们得到等式 W 0 ∗ g r a y _ l e v e l 0 + W 1 ∗ g r a y _ l e v e l 1 = = t o t a l _ g r a y W0*gray\_level0+W1*gray\_level1==total\_gray W0∗gray_level0+W1∗gray_level1==total_gray |
| 4.如果我们想将两个 前/后 景分开,则我们可以立马想到类间方差!没错,就是统计课上的类间方差。 |
| 5.将等式3代入类间方差公式 σ 2 = W 0 ( g r a y _ l e v e l 0 − t o t a l _ g r a y ) 2 + W 1 ( g r a y _ l e v e l 1 − t o t a l _ g r a y ) 2 \sigma^2=W0(gray\_level0-total\_gray)^2+W1(gray\_level1-total\_gray)^2 σ2=W0(gray_level0−total_gray)2+W1(gray_level1−total_gray)2 |
| 6.得到等式 σ 2 = = W 0 W 1 ( g r a y _ l e v e l 0 − g r a y _ l e v e l 1 ) 2 \sigma^2==W0W1(gray\_level0-gray\_level1)^2 σ2==W0W1(gray_level0−gray_level1)2 |
七、完整代码
class OTSUTransformer():
np.seterr(invalid='ignore')
# Convert BGR to GRAY
@staticmethod
def BGR2GRAY(img):
gray_img = 0.2126 * img[:, :, 0] + 0.7152 * img[:, :, 1] + 0.0722 * img[:, :, 2]
return np.array(gray_img).astype(np.uint8)
# OTSU
@staticmethod
def OTSU(img):
#BGR转GRAY图像
gray = 0.2126 * img[:, :, 0] + 0.7152 * img[:, :, 1] + 0.0722 * img[:, :, 2]
#将图像在长款上各缩短到1/4,以加快查找阈值
gray_img = gray[::4, ::4]
gray_img = np.array(gray_img).astype(np.uint8)
gray_level0 = np.zeros(256, dtype=np.float)
gray_level1 = np.zeros(256, dtype=np.float)
w0 = np.zeros(256, dtype=np.float)
w1 = np.zeros(256, dtype=np.float)
threshold = np.arange(256).astype(np.uint8)
y_size, x_size = np.shape(gray_img)
#为了更进一步加快大津法,range在最小值和最大值中间,且步长为2
for i in range(gray_img.min(), gray_img.max(), 2):
#计算 前/后 景的像素所占比例
w0[i] = np.shape(gray_img[gray_img > threshold[i]])[0] / (y_size*x_size)
#计算 前/后 景的像素的平均值
gray_level0[i] = np.mean(gray_img[gray_img > threshold[i]])
gray_level1[i] = np.mean(gray_img[gray_img <= threshold[i]])
w1[:] = 1 - w0[:]
#计算在不同阈值情况下的 类间方差
var = np.array(w0[:]*w1[:]*(gray_level0[:]-gray_level1[:])**2).astype(np.uint8)
#最优的阈值对应的是最大的 类间方差
best_threshold = threshold[np.argmax(var)]
#通过最优阈值来二值化
gray[gray<best_threshold] = 0
gray[gray>=best_threshold] = 255
# 通过最优阈值来二值化
gray[gray < best_threshold] = 0
gray[gray >= best_threshold] = 255
cv2.imwrite('res.jpg', gray)