机器学习——决策树
引言
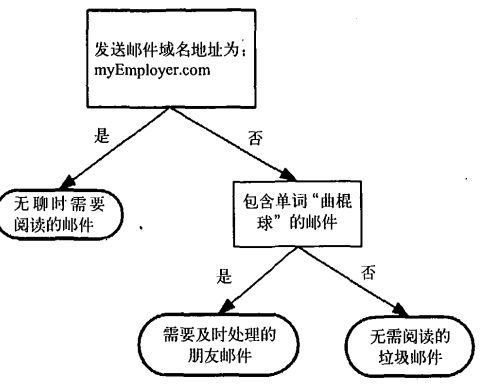
邮件分类系统:首先检测发送邮件域名地址,如果地址为MyEmployer.com则将其放在分类“无聊时需要阅读的邮件”中。如果邮件不是来自这个域名,则检查邮件内容里是否包含单词曲棍球,如果包含则将邮件归类到“需要及时处理的朋友邮件”,如果不包含则将邮件归类到“无需阅读的垃圾邮件”。
思路
(1)从一堆原始数据中构造决策树,首先我们讨论构造决策树的方法,编写构造树的python代码;
(2)度量算法成功率的方法;
(3)使用递归建立分类器,并使用Matplotlib绘制决策树图;
(4)输入一些隐性眼镜的处方数据,并由决策树分类器预测需要的镜片类型。
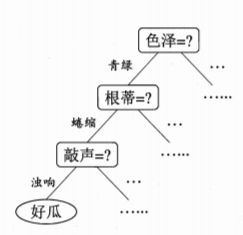
当决策树采用二分法划分数据时,决策树的大致结构如图所示:
但是大部分时候,并不采用这种方法。如何选择最优划分属性,看划分能力有没有提升,故定义了一个信息增益。
信息增益
(在划分数据之前之后信息发现的变化称为信息增益)
简介
(1)划分数据集的最大原则:将无序的数据变得更加有序。
(2)好处:通过计算信息增益,计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的划分。
如何计算信息增益?
(1)度量方式称为为香农熵;
(2)![]()
![]() 所有的类别所有可能包含的期望值
所有的类别所有可能包含的期望值![]() 其中n是分类的数目。
其中n是分类的数目。
计算数据集的熵(信息熵):
# -*- coding: utf-8 -*-
__author__ = 'Mouse'
from math import log
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
print "numEntries:", numEntries
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1] #取dataSet最后的一列数据
if currentLabel not in labelCounts.keys():labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
print " labelCounts:",labelCounts # {'yes': 2, 'no': 3}
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries #如 yes: 2/5=0.4 如no :3/5=0.6
print key, ":", prob
shannonEnt -= prob * log(prob, 2) #log base 2
print key, ":", shannonEnt
return shannonEnt
if __name__ == '__main__':
dataSet, labels = createDataSet()
shannonEnt = calcShannonEnt(dataSet)
print shannonEnt
E:\Anaconda\python.exe E:/WorkSpace/py/algorithms/study/learn.py
numEntries: 5
labelCounts: {'yes': 2, 'no': 3}
yes : 0.4
yes : 0.528771237955
no : 0.6
no : 0.970950594455
0.970950594455(正例子 yes+反例子no)numEntries: 6
labelCounts: {'maybe': 1, 'yes': 2, 'no': 3}
maybe : 0.166666666667
maybe : 0.430827083454
yes : 0.333333333333
yes : 0.959147917027
no : 0.5
no : 1.45914791703
1.45914791703 (正例子yes+反例子no)得到信息熵之后,就可以按照获取最大信息增益的方法划分数据集。
划分数据集
想象在一个二维空间的数据散点图,需要在数据之间画条线,将它们分成两个部分。
#dataSet是待划分的数据集、划分数据集的特征、特征的返回值
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value: # 取出每行的第一个元素进行比较
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSetretDataSet = splitDataSet(dataSet, 0, 0)
print retDataSet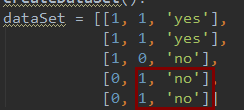
遍历整个数据集,循环计算机香农熵和splitDataSet()函数,找到最好的特征划分方式。熵的计算会告诉我们如何划分数据集是最好的数据组织方式。
就是指找到最好的信息增益,信息增益越大,对应的那个特征属性就是最好的划分。
构建决策树
使用Matplotlib注解绘制树形图。决策树的优点就是直观易于理解。
Matplotlib的使用方法:http://blog.csdn.net/ywjun0919/article/details/8692018
__author__ = 'Mouse'
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': #test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
# if you do get a dictonary you know it's a tree, and the first element will be another dict
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0;
plotTree(inTree, (0.5, 1.0), '')
plt.show()
#def createPlot():
# fig = plt.figure(1, facecolor='white')
# fig.clf()
# createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
# plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
# plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
# plt.show()
# def retrieveTree(i):
# listOfTrees = [{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
# {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
# ]
# return listOfTrees[i]
#createPlot(thisTree)# -*- coding: utf-8 -*-
__author__ = 'Mouse'
from math import log
import operator
import treePlotter
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
# print "numEntries:", numEntries
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1] #取dataSet最后的一列数据
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
#print " labelCounts:", labelCounts # {'yes': 2, 'no': 3}
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries #如 yes: 2/5=0.4 如no :3/5=0.6
#print key, ":", prob
shannonEnt -= prob * log(prob, 2) #log base 2
#print key, ":", shannonEnt
return shannonEnt
# dataSet是待划分的数据集、划分数据集的特征、特征的返回值
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value: # 取出每行的第一个元素进行比较
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
reducedFeatVec.extend(featVec[axis + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet)
print baseEntropy
bestInfoGain = 0.0;
bestFeature = -1
for i in range(numFeatures): #iterate over all the features
featList = [example[i] for example in dataSet] #create a list of all the examples of this feature
uniqueVals = set(featList) #get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): #compare this to the best gain so far
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i
return bestFeature #returns an integer
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0] #stop splitting when all of the classes are equal
if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel: {}}
del (labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
#使用决策树执行分类函数
def classify(inputTree,featLabels,testVec):
firstStr = inputTree.keys()[0]
secondDict = inputTree[firstStr]
if firstStr in featLabels:
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:#比较特征值,决策树是根据特征的值划分的
if type(secondDict[key]).__name__=='dict':#比较是否到达叶结点
classLabel = classify(secondDict[key],featLabels,testVec)#递归调用
else: classLabel = secondDict[key]
return classLabel
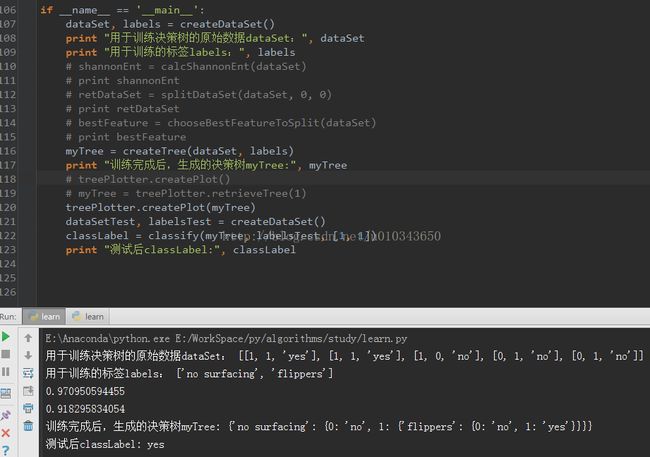
if __name__ == '__main__':
dataSet, labels = createDataSet()
print "用于训练决策树的原始数据dataSet:", dataSet
print "用于训练的标签labels:", labels
# shannonEnt = calcShannonEnt(dataSet)
# print shannonEnt
# retDataSet = splitDataSet(dataSet, 0, 0)
# print retDataSet
# bestFeature = chooseBestFeatureToSplit(dataSet)
# print bestFeature
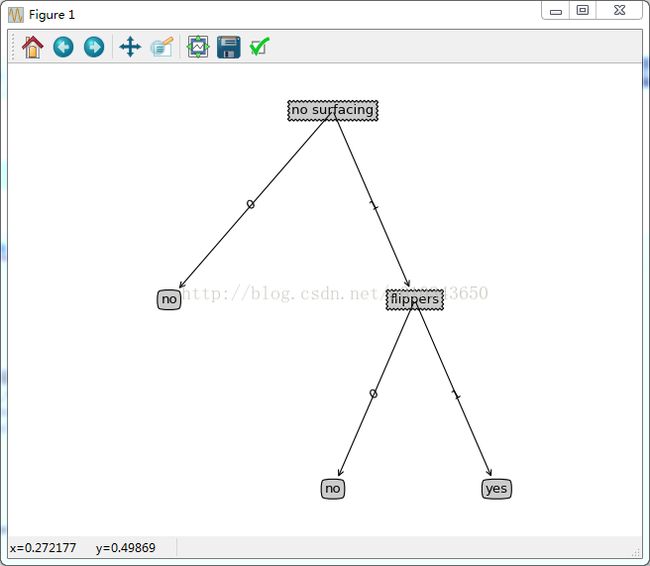
myTree = createTree(dataSet, labels)
print "训练完成后,生成的决策树myTree:", myTree
# treePlotter.createPlot()
# myTree = treePlotter.retrieveTree(1)
treePlotter.createPlot(myTree)
dataSetTest, labelsTest = createDataSet()
classLabel = classify(myTree, labelsTest, [1, 1])
print "测试后classLabel:", classLabel
测试
然后测试[1,1] :
决策树的存储
构造决策树是很耗时的任务,即使处理很小的数据集。如果数据集很大,将会耗很多的时间。然而用创建好决策树解决分类问题,则可以很快完成。
因此,为了节省计算时间,最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题,需要使用Python模块Picker序列化操作,字典对象也不例外。
def storeTree(inputTree,filename):
import pickle
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename)
return pickle.load(fr)使用的数据:
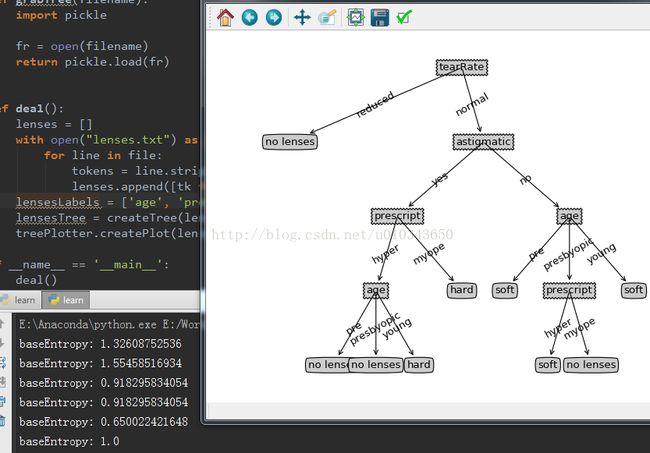
def deal():
lenses = []
with open("lenses.txt") as file:
for line in file:
tokens = line.strip().split('\t')
lenses.append([tk for tk in tokens])
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = createTree(lenses, lensesLabels)
treePlotter.createPlot(lensesTree)使用算法ID3生成的决策树:
------------------------------------------------------------------------------------------------------------------------------------------------------------------------
0,11,111,1111,11111,111111,0,0.460,yes 1,11,222,1111,11111,111111,0,0.376,yes 1,11,111,1111,11111,111111,0,0.264,yes 0,11,222,1111,11111,111111,0,0.318,yes 2,11,111,1111,11111,111111,0,0.215,yes 0,22,111,1111,22222,222222,0,0.237,yes 1,22,111,2222,22222,222222,0,0.149,yes 1,22,111,1111,22222,111111,0,0.211,yes 1,22,222,2222,22222,111111,0,0.091,no 0,33,333,1111,33333,222222,1,0.267,no 2,33,333,3333,33333,111111,1,0.057,no 2,11,111,3333,33333,222222,1,0.099,no 0,22,111,2222,11111,111111,0,0.161,no 2,22,222,2222,11111,111111,0,0.198,no 1,22,111,1111,22222,222222,1,0.370,no 2,11,111,3333,33333,111111,0,0.042,no 0,11,222,2222,22222,111111,0,0.103,no
# -*- coding: utf-8 -*-
"""
Created on Sat Sep 10 20:09:11 2016
@file trees.py
@brief 决策树算法实现 实现西瓜案例 改进
在上一个tree.py版本中无法对连续属性进行处理,西瓜案例中的密度与含糖度两个属性是连续数据,那该如何处理呢
@version V1.1
"""
"""
@brief 计算给定数据集的信息熵
@param dataSet 数据集
@return 香农熵
"""
import operator
import copy
from math import log
def calcShannonEnt(dataSet):
numEntries = len(dataSet)#求取数据集的行数
labelCounts = {}
for featVec in dataSet:#读取数据集中的一行数据
currentLabel = featVec[-1] #取featVec中最后一列的值
#以一行数据中的最后一列值为键值进行统计
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries#将每一类求取概率
shannonEnt -= prob * log(prob,2)#求取数据集的香农熵
return shannonEnt
"""
@brief 划分数据集 按照给定的特征划分数据集
@param[in] dataSet 待划分的数据集
@param[in] axis 划分数据集的特征
@param[in] value 需要返回的特征的值
@return retDataSet 返回划分后的数据集
"""
def splitDataSet(dataSet, axis, value):
retDataSet = []#返回的划分后的数据集
for featVec in dataSet:
#抽取符合划分特征的值
if featVec[axis] == value:
#如何符合此特征值 则存储,存储划分后的数据集时 不需要存储选为划分的特征
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1 :])
retDataSet.append(reducedFeatVec)
return retDataSet
"""
@brief 与上述函数类似,区别在于上述函数是用来处理离散特征值而这里是处理连续特征值
对连续变量划分数据集,direction规定划分的方向,
决定是划分出小于value的数据样本还是大于value的数据样本集
"""
def splitContinuousDataSet(dataSet,axis,value,direction):
retDataSet=[]
for featVec in dataSet:
if direction==0:
if featVec[axis]>value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
else:
if featVec[axis]<=value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
"""
@brief 针对离散属性 遍历整个数据集,循环计算香农熵和选择划分函数,找到最好的划分方式。
对于连续属性需要做处理
决策树算法中比较核心的地方,究竟是用何种方式来决定最佳划分?
使用信息增益作为划分标准的决策树称为ID3
使用信息增益率比作为划分标准的决策树称为C4.5
本程序为信息增益的ID3树
从输入的训练样本集中,计算划分之前的熵,找到当前有多少个特征,遍历每一个特征计算信息增益,找到这些特征中能带来信息增益最大的那一个特征。
这里用分了两种情况,离散属性和连续属性
1、离散属性,在遍历特征时,遍历训练样本中该特征所出现过的所有离散值,假设有n种取值,那么对这n种我们分别计算每一种的熵,最后将这些熵加起来
就是划分之后的信息熵
2、连续属性,对于连续值就稍微麻烦一点,首先需要确定划分点,用二分的方法确定(连续值取值数-1)个切分点。遍历每种切分情况,对于每种切分,
计算新的信息熵,从而计算增益,找到最大的增益。
假设从所有离散和连续属性中已经找到了能带来最大增益的属性划分,这个时候是离散属性很好办,直接用原有训练集中的属性值作为划分的值就行,但是连续
属性我们只是得到了一个切分点,这是不够的,我们还需要对数据进行二值处理。
@param[in] dataSet 整个特征集 待选择的集
@return bestFeature 划分数据集最好的划分特征列的索引值
"""
def chooseBestFeatureToSplit(dataSet, labels):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
bestSplitDict = {}
for i in range(numFeatures):
# 对连续型特征进行处理 ,i代表第i个特征,featList是每次选取一个特征之后这个特征的所有样本对应的数据
featList = [example[i] for example in dataSet]
#因为特征分为连续值和离散值特征,对这两种特征需要分开进行处理。
#if type(featList[0]).__name__ == 'float' or type(featList[0]).__name__ == 'int':
if isinstance(featList[0],float) == True or isinstance(featList[0],int) == True:
# 产生n-1个候选划分点
sortfeatList = sorted(featList)
splitList = []
for j in range(len(sortfeatList) - 1):
splitList.append((sortfeatList[j] + sortfeatList[j + 1]) / 2.0)
bestSplitEntropy = 10000
# 求用第j个候选划分点划分时,得到的信息熵,并记录最佳划分点 找到最大信息熵的划分
for value in splitList:
newEntropy = 0.0
#根据value将属性集分为两个部分
subDataSet0 = splitContinuousDataSet(dataSet, i, value, 0)
subDataSet1 = splitContinuousDataSet(dataSet, i, value, 1)
prob0 = len(subDataSet0) / float(len(dataSet))
newEntropy += prob0 * calcShannonEnt(subDataSet0)
prob1 = len(subDataSet1) / float(len(dataSet))
newEntropy += prob1 * calcShannonEnt(subDataSet1)
if newEntropy < bestSplitEntropy:
bestSplitEntropy = newEntropy
bestSplit = value
# 用字典记录当前特征的最佳划分点
bestSplitDict[labels[i]] = bestSplit
infoGain = baseEntropy - bestSplitEntropy
# 对离散型特征进行处理
else:
uniqueVals = set(featList)
newEntropy = 0.0
# 计算该特征下每种划分的信息熵,选取第i个特征的值为value的子集
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i
# 若当前节点的最佳划分特征为连续特征,则将其以之前记录的划分点为界进行二值化处理
# 即是否小于等于bestSplitValue,例如将密度变为密度<=0.3815
#将属性变了之后,之前的那些float型的值也要相应变为0和1
if type(dataSet[0][bestFeature]).__name__=='float' or type(dataSet[0][bestFeature]).__name__ == 'int':
bestSplitValue = bestSplitDict[labels[bestFeature]]
labels[bestFeature] = labels[bestFeature] + '<=' + str(bestSplitValue)
for i in range(len(dataSet)):
if dataSet[i][bestFeature] <= bestSplitValue:
dataSet[i][bestFeature] = 1
else:
dataSet[i][bestFeature] = 0
return bestFeature
"""
@brief 计算一个特征数据列表中 出现次数最多的特征值以及次数
@param[in] 特征值列表
@return 返回次数最多的特征值
例如:[1,1,0,1,1]数据列表 返回 1
0"""
def majorityCnt(classList):
classCount = {}
#统计数据列表中每个特征值出现的次数
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
#根据出现的次数进行排序 key=operator.itemgetter(1) 意思是按照次数进行排序
#classCount.items() 转换为数据字典 进行排序 reverse = True 表示由大到小排序
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse = True)
#返回次数最多的一项的特征值
return sortedClassCount[0][0]
"""
@brief 主程序,递归产生决策树。
params:
dataSet:用于构建树的数据集,最开始就是data_full,然后随着划分的进行越来越小,第一次划分之前是17个瓜的数据在根节点,然后选择第一个bestFeat是纹理
纹理的取值有清晰、模糊、稍糊三种,将瓜分成了清晰(9个),稍糊(5个),模糊(3个),这个时候应该将划分的类别减少1以便于下次划分
labels:还剩下的用于划分的类别
data_full:全部的数据
label_full:全部的类别
既然是递归的构造树,当然就需要终止条件,终止条件有三个:
1、当前节点包含的样本全部属于同一类别;-----------------注释1就是这种情形
2、当前属性集为空,即所有可以用来划分的属性全部用完了,这个时候当前节点还存在不同的类别没有分开,这个时候我们需要将当前节点作为叶子节点,
同时根据此时剩下的样本中的多数类(无论几类取数量最多的类)-------------------------注释2就是这种情形
3、当前节点所包含的样本集合为空。比如在某个节点,我们还有10个西瓜,用大小作为特征来划分,分为大中小三类,10个西瓜8大2小,因为训练集生成
树的时候不包含大小为中的样本,那么划分出来的决策树在碰到大小为中的西瓜(视为未登录的样本)就会将父节点的8大2小作为先验同时将该中西瓜的
大小属性视作大来处理。
构
"""
def createTree(dataSet,labels,data_full,labels_F):
#注意label和labels_full可能是同一参数 这样就会导致删除了labels_full
#因此在此处使用深拷贝 解决此类问题
labels_full = copy.deepcopy(labels_F)
classList=[example[-1] for example in dataSet]
if classList.count(classList[0])==len(classList): #注释1
return classList[0]
if len(dataSet[0])==1: #注释2
return majorityCnt(classList)
#平凡情况,每次找到最佳划分的特征
bestFeat=chooseBestFeatureToSplit(dataSet, labels)
bestFeatLabel=labels[bestFeat]
myTree={bestFeatLabel:{}}
featValues=[example[bestFeat] for example in dataSet]
'''''
刚开始很奇怪为什么要加一个uniqueValFull,后来思考下觉得应该是在某次划分,比如在根节点划分纹理的时候,将数据分成了清晰、模糊、稍糊三块
,假设之后在模糊这一子数据集中,下一划分属性是触感,而这个数据集中只有软粘属性的西瓜,这样建立的决策树在当前节点划分时就只有软粘这一属性了,
事实上训练样本中还有硬滑这一属性,这样就造成了树的缺失,因此用到uniqueValFull之后就能将训练样本中有的属性值都囊括。
如果在某个分支每找到一个属性,就在其中去掉一个,最后如果还有剩余的根据父节点投票决定。
但是即便这样,如果训练集中没有出现触感属性值为“一般”的西瓜,但是分类时候遇到这样的测试样本,那么应该用父节点的多数类作为预测结果输出。
'''
uniqueVals=set(featValues)
if type(dataSet[0][bestFeat]).__name__=='str':
# currentlabel=labels_full.index(labels[bestFeat])
#找到此标签在原始标签中的索引
currentlabel=labels_full.index(bestFeatLabel)
featValuesFull=[example[currentlabel] for example in data_full]
uniqueValsFull=set(featValuesFull)
del(labels[bestFeat])
'''''
针对bestFeat的每个取值,划分出一个子树。对于纹理,树应该是{"纹理":{?}},显然?处是纹理的不同取值,有清晰模糊和稍糊三种,对于每一种情况,
都去建立一个自己的树,大概长这样{"纹理":{"模糊":{0},"稍糊":{1},"清晰":{2}}},对于0\1\2这三棵树,每次建树的训练样本都是值为value特征数减少1
的子集。
'''
for value in uniqueVals:
subLabels = labels[:]
if type(dataSet[0][bestFeat]).__name__ == 'str':
uniqueValsFull.remove(value)
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, data_full, labels_full)
#完成对缺失值的处理
if type(dataSet[0][bestFeat]).__name__ == 'str':
for value in uniqueValsFull:
myTree[bestFeatLabel][value] = majorityCnt(classList)
return myTree
"""
@brief 对未知特征在创建的决策树上进行分类
@param[in] inputTree
@param[in] featLabels
@param[in] testVec
@return classLabel 返回识别的结果
"""
def classify(inputTree,featLabels,testVec):
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key :
if isinstance(secondDict[key],dict) == True:
classLabel = classify(secondDict[key],featLabels,testVec)
else:
classLabel = secondDict[key]
return classLabel
"""
@brief 存储构建的决策树
"""
def storeTree(inputTree,filename):
import pickle
fw = open(filename,'wb')
pickle.dump(inputTree,fw)
fw.close()
"""
@brief 读取文本存储的决策树
"""
def grabTree(filename):
import pickle
fr = open(filename, 'rb')
return pickle.load(fr)__author__ = 'Mouse'
import sys
reload(sys)
sys.setdefaultencoding('utf8')
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):
numLeafs = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': # test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt): # if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[
key]).__name__ == 'dict': #test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key], cntrPt, str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalW;
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show()# -*- coding: utf-8 -*-
import sys
reload(sys)
sys.setdefaultencoding('utf8')
import a
import treePlotter
if __name__ == '__main__':
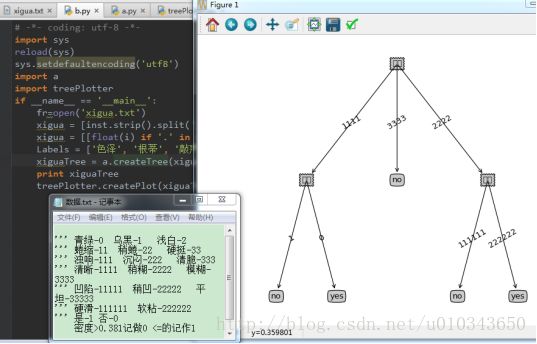
fr=open('xigua.txt')
xigua = [inst.strip().split(',') for inst in fr.readlines()]
xigua = [[float(i) if '.' in i else i for i in row] for row in xigua] # change decimal from string to float
Labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率']
xiguaTree = a.createTree(xigua, Labels, xigua, Labels)
print xiguaTree
treePlotter.createPlot(xiguaTree)