决策树——剪枝处理
剪枝处理
1:剪枝处理的原因
“剪枝”是决策树学习算法对付“过拟合”的主要手段,因此,可通过“剪枝”来一定程度避免因决策分支过多,以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合
2:剪枝的基本策略
预剪枝、后剪枝
3:剪枝后效果如何判断
判断决策树泛化性能是否提升的方法采用留出法,即预留一部分数据用作“验证集”以进行性能评估
5:预剪枝(通过提前停止树的构建而对树剪枝)
(1)预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛华性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点。
(2)主要方法:
1.当决策树达到预设的高度时就停止决策树的生长
2.达到某个节点的实例具有相同的特征向量,即使这些实例不属 于同一类,也可以停止决策树的生长。
3.定义一个阈值,当达到某个节点的实例个数小于阈值时就可以 停止决策树的生长。
4.通过计算每次扩张对系统性能的增益,决定是否停止决策树的 生长。
(3)例子:
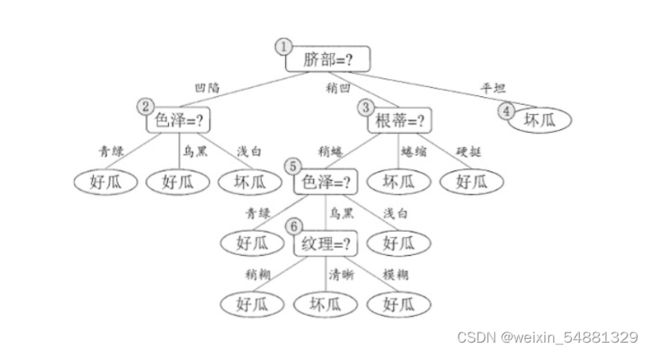
这个数据集根据信息增益可以构造出一颗未剪枝的决策树:
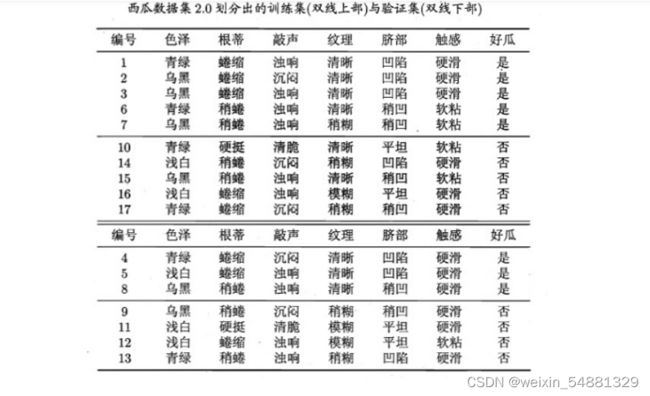
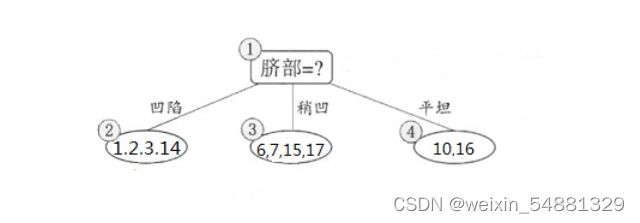
前面博客讲过用信息增益怎么构造决策树,这边还是用信息增益构造决策树,先来计算出所有特征的信息增益值,通过计算因为色泽和脐部的信息增益值最大,所以从这两个中随机挑选一个,这里选择 脐部来对数据集进行划分,这会产生三个分支,如下图所示:
下面来看看是否要用脐部进行划分, 划分前:所有样本都在根节点,把该结点标记为叶结点,其类别标记为训练集中样本数量最多的类别,因此标记为 好瓜,然后用验证集对其性能评估,可以看出样本{4,5,8}被正确分类,其他被错误分类,因此精度为43.9%。 划分后: 划分后的的决策树为: 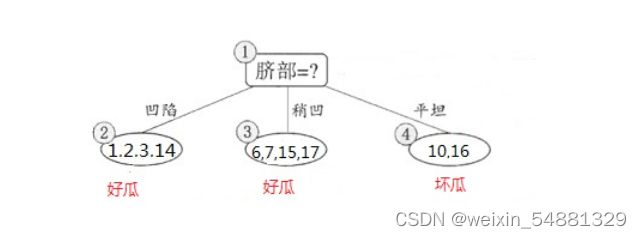
则验证集在这颗决策树上的精度为:5/7 = 71.4% > 42.9%。因此,用 脐部 进行划分。
接下来,决策树算法对结点 (2) 进行划分,再次使用信息增益挑选出值最大的那个特征,这里我就不算了,计算方法和上面类似,信息增益值最大的那个特征是“色泽”,则使用“色泽”划分后决策树为: 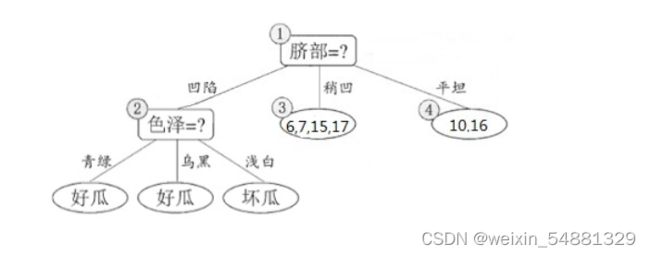
但到底该不该划分这个结点,还是要用验证集进行计算,可以看到划分后,精度为:5/7=0.571<0.714,因此,预剪枝策略将禁止划分结点 (2) 。对于结点 (3) 最优的属性为“根蒂”,划分后验证集精度仍为71.4%,因此这个划分不能提升验证集精度,所以预剪枝将禁止结点 (3) 划分。对于结点 (4) ,其所含训练样本已属于同一类,所以不再进行划分。
所以基于预剪枝策略生成的最终的决策树为:
(4) 预剪枝的优缺点
优点:降低过拟合风险,显著减少训练时间和测试时间开销。
缺点 :欠拟合风险,有些分支的当前划分虽然不能提升泛化性能,但 在其基础上进行的后续划分却有可能显著提高性能。预剪枝基于 “贪心”本质禁止这些分支展开,带来了欠拟合风险。
6:后剪枝
(1)后剪枝就是先构造一颗完整的决策树,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛华性能的提升,则把该子树替换为叶结点。前面已经说过了,使用前面给出的训练集会生成一颗(未剪枝)决策树:
后剪枝算法首先考察上图中的结点 (6),若将以其为根节点的子树删除,即相当于把结点 (6) 替换为叶结点,替换后的叶结点包括编号为{7,15}的训练样本,因此把该叶结点标记为“好瓜”(因为这里正负样本数量相等,所以随便标记一个类别),因此此时的决策树在验证集上的精度为57.1%(为剪枝的决策树为42.9%),所以后剪枝策略决定剪枝,剪枝后的决策树如下图所示:
后剪枝算法首先考察上图中的结点 (6),若将以其为根节点的子树删除,即相当于把结点 (6) 替换为叶结点,替换后的叶结点包括编号为{7,15}的训练样本,因此把该叶结点标记为“好瓜”(因为这里正负样本数量相等,所以随便标记一个类别),因此此时的决策树在验证集上的精度为57.1%(为剪枝的决策树为42.9%),所以后剪枝策略决定剪枝,剪枝后的决策树如下图所示:

接着考察结点 5,同样的操作,把以其为根节点的子树替换为叶结点,替换后的叶结点包含编号为{6,7,15}的训练样本,根据“多数原则”把该叶结点标记为“好瓜”,测试的决策树精度认仍为57.1%,所以不进行剪枝。
考察结点 2 ,和上述操作一样,不多说了,叶结点包含编号为{1,2,3,14}的训练样本,标记为“好瓜”,此时决策树在验证集上的精度为71.4%,因此,后剪枝策略决定剪枝。剪枝后的决策树为:
接着考察结点 3 ,同样的操作,剪枝后的决策树在验证集上的精度为71.4%,没有提升,因此不剪枝;对于结点 1 ,剪枝后的决策树的精度为42.9%,精度下降,因此也不剪枝。
因此,基于后剪枝策略生成的最终的决策树如上图所示,其在验证集上的精度为71.4%。
(2)后剪枝的优缺点
优点 :后剪枝比预剪枝保留了更多的分支,欠拟合风险小 ,泛化性能往往优于预剪枝决策树
缺点:训练时间开销大,后剪枝过程是在生成完全决策树 之后进行的,需要自底向上对所有非叶结点逐一计算
7:代码实现:
D_keys = {
'色泽': ['青绿', '乌黑', '浅白'],
'根蒂': ['蜷缩', '硬挺', '稍蜷'],
'敲声': ['清脆', '沉闷', '浊响'],
'纹理': ['稍糊', '模糊', '清晰'],
'脐部': ['凹陷', '稍凹', '平坦'],
'触感': ['软粘', '硬滑'],
}
keys = ['是', '否']
#划分训练集&测试集,留出法,比例为7:3,分层抽样
def traintest(dataSet):
dataSet0 = dataSet[dataSet['好瓜'] == '是']
dataSet1 = dataSet[dataSet['好瓜'] == '否']
list0 = dataSet0.sample(frac=0.7)
list0 = list0.append(dataSet1.sample(frac=0.7))
rowlist = []
for indexs in list0.index:
rowlist.append(indexs)
list1 = dataSet.drop(rowlist, axis=0)
return list0,list1
# 叶节点选择其类别为D中样本最多的类
def choose_largest_example(D):
count = D['好瓜'].value_counts()
return '是' if count['是'] > count['否'] else '否'
# 测试决策树的准确率
def test_Tree(Tree, data_test):
accuracy = 0
for index, row in data_test.iterrows():
result = dfs_Tree(Tree, row)
if result == row['好瓜']:
# print(row.values, Tree)
accuracy += 1
return accuracy / data_test.shape[0]
# 判断D中的样本在A上的取值是否相同
def same_value(D, A):
for key in A:
if key in D_keys and len(D[key].value_counts()) > 1:
return False
return True
# 计算给定数据集的熵
def calc_Ent(dataSet):
numEntries = dataSet['power'].sum()
Count = dataSet.groupby('好瓜')['power'].sum()
Ent = 0.0
for key in keys:
# print(Count[key])
if key not in Count:
Ent -= 0.0
else:
prob = Count[key] / numEntries
Ent -= prob * math.log(prob, 2)
return Ent
# 计算按key划分的信息增益值
def calc_Gain_D(D, D_no_nan, key, Ent_D):
Ent = 0.0
D_size = D['power'].sum()
D_nan_size = D_no_nan['power'].sum()
for value in D_keys[key]:
Dv = D.loc[D[key] == value]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size / D_nan_size * Ent_Dv
return D_nan_size / D_size * (Ent_D - Ent)
# 生成连续值属性的候选划分点集合T
def candidate_T(D, key, n):
L = set(D[key])
T = []
a, Sum = 0, 0
for value in L:
Sum += value
a += 1
if a == n:
T.append(Sum / n)
a, Sum = 0, 0
if a > 0:
T.append(Sum / a)
return T
# 计算样本D基于划分点t二分后的连续值属性信息增益
def calc_Gain_t(D, D_no_nan, key, t, Ent_D):
Ent = 0.0
D_size = D['power'].sum()
D_nan_size = D_no_nan['power'].sum()
Dv = D.loc[D[key] <= t]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size / D_nan_size * Ent_Dv
Dv = D.loc[D[key] > t]
Dv_size = Dv['power'].sum()
Ent_Dv = calc_Ent(Dv)
Ent += Dv_size / D_nan_size * Ent_Dv
return D_nan_size / D_size * (Ent_D - Ent)
# 计算样本D基于不同划分点t二分后的连续值属性信息增益,找出最大增益划分点
def calc_Gain_C(D, D_no_nan, key, Ent_D):
n = 2
T = candidate_T(D, key, n)
max_Gain, max_partition = -1, -1
for t in T:
Gain = calc_Gain_t(D, D_no_nan, key, t, Ent_D)
if max_Gain < Gain:
max_Gain = Gain
max_partition = t
return max_Gain, max_partition
# 从A中选择最优的划分属性值,若为连续值,返回划分点
def choose_best_attribute(D, A):
max_Gain, max_partition, partition, best_attr = -1, -1, -1, ''
for key in A:
# 划分属性为离散属性时
if key in D_keys:
D_no_nan = D.loc[pd.notna(D[key])]
Ent_D = calc_Ent(D_no_nan)
Gain = calc_Gain_D(D, D_no_nan, key, Ent_D)
# 划分属性为连续属性时
else:
D_no_nan = D.loc[pd.notna(D[key])]
Ent_D = calc_Ent(D_no_nan)
Gain, partition = calc_Gain_C(D, D_no_nan, key, Ent_D)
if max_Gain < Gain:
best_attr = key
max_Gain = Gain
max_partition = partition
return best_attr, max_partition
# 函数TreeGenerate 递归生成决策树,以下情形导致递归返回
# 1. 当前结点包含的样本全属于一个类别
# 2. 当前属性值为空, 或是所有样本在所有属性值上取值相同,无法划分
# 3. 当前结点包含的样本集合为空,不可划分
def TreeGenerate(D, A):
Count = D['好瓜'].value_counts()
if len(Count) == 1:
return D['好瓜'].values[0]
if len(A) == 0 or same_value(D, A):
return choose_largest_example(D)
node = {}
best_attr, partition = choose_best_attribute(D, A)
D_size = D.shape[0]
# 最优划分属性为离散属性时
if best_attr in D_keys:
for value in D_keys[best_attr]:
Dv = D.loc[D[best_attr] == value].copy()
Dv_size = Dv.shape[0]
Dv.loc[pd.isna(Dv[best_attr]), 'power'] = Dv_size / D_size
temp1 = test_Tree(choose_largest_example(D),data_test)
if Dv.shape[0] == 0:
node[value] = choose_largest_example(D)
else:
new_A = [key for key in A if key != best_attr]
node[value] = TreeGenerate(Dv, new_A)
temp0 = test_Tree(node[value],data_test)
if temp1 > temp0:
node[value] = choose_largest_example(D)
# 最优划分属性为连续属性时
else:
# print(best_attr, partition)
# print(D.values)
left = D.loc[D[best_attr] <= partition].copy()
Dv_size = left.shape[0]
left.loc[pd.isna(left[best_attr]), 'power'] = Dv_size / D_size
left_key = '<= ' + str(partition)
if left.shape[0] == 0:
node[left_key] = choose_largest_example(D)
else:
node[left_key] = TreeGenerate(left, A)
right = D.loc[D[best_attr] > partition].copy()
Dv_size = right.shape[0]
right.loc[pd.isna(right[best_attr]), 'power'] = Dv_size / D_size
right_key = '> ' + str(partition)
temp1 = test_Tree(choose_largest_example(D), data_test)
if right.shape[0] == 0:
node[right_key] = choose_largest_example(D)
else:
node[right_key] = TreeGenerate(right, A)
temp0 = test_Tree(node[right_key], data_test)
if temp1 > temp0:
node[right_key] = choose_largest_example(D)
# plotTree.plotTree(Tree)
return {best_attr: node}
# 获得下一层子树分支
def get_next_Tree(Tree, key, value):
if key not in D_keys:
partition = float(list(Tree[key].keys())[0].split(' ')[1])
if value <= partition:
value = '<= ' + str(partition)
else:
value = '> ' + str(partition)
return Tree[key][value]
# 深度优先遍历,判断预测值
def dfs_Tree(Tree, row):
if type(Tree).__name__ == 'dict':
key = list(Tree.keys())[0]
value = row[key]
if pd.isnull(value):
result = {key: 0 for key in D_keys['好瓜']}
for next_key in Tree[key]:
next_Tree = Tree[key][next_key]
temp = dfs_Tree(next_Tree, row)
result[temp] += 1
return '是' if count['是'] > count['否'] else '否'
else:
next_Tree = get_next_Tree(Tree, key, value)
return dfs_Tree(next_Tree, row)
else:
return Tree
if __name__ == '__main__':
# 读取数据
filename = '/Users/haoranjiang/Documents/machine learning/111111111/tree.txt'
dataSet = loadData(filename)
dataSet.drop(columns=['编号'], inplace=True)
# 考虑缺失值
dataSet['power'] = 1.0
data_train,data_test = traintest(dataSet)
# 决策树训练
A = [column for column in data_train.columns if column != '好瓜']
Tree = TreeGenerate(data_train, A)
# 决策树测试
print('准确度:',test_Tree(Tree, data_test)*100,'%')
print(Tree)