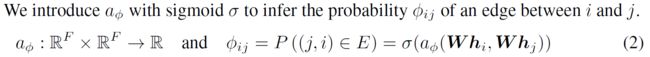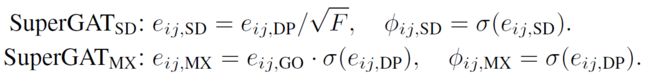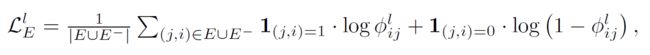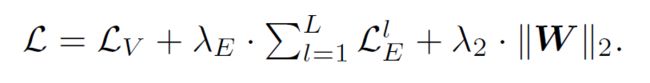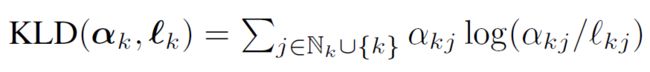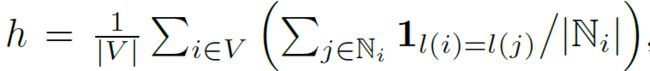文献阅读(39)ICLR2021-How to Find Your Friendly Neighborhood:Graph Attention Design with Self-supervision
本文是对《How to Find Your Friendly Neighborhood:Graph Attention Design with Self-supervision》一文的浅显翻译与理解,如有侵权即刻删除。
朋友们,我们在github创建了一个图学习笔记库,总结了相关文章的论文、代码和我个人的中文笔记,能够帮助大家更加便捷地找到对应论文,欢迎star~
Chinese-Reading-Notes-of-Graph-Learning
更多相关文章,请移步:文献阅读总结:网络表示学习/图学习
文章目录
- Title
- 总结
-
- 1 模型
-
- 1.1 定义
- 1.2 注意力设计方案
- 2 实验
-
- 2.1 注意力学习节点标签一致性吗
- 2.2 注意力能预测边是否存在吗
- 2.3 哪种注意力设计适合运用在网络上
- 2.4 这种结论对现实数据集有效吗
Title
《How to Find Your Friendly Neighborhood:Graph Attention Design with Self-supervision》
——ICLR2021
Author: Dongkwan Kim
总结
文章提出了自监督的注意力网络SuperGAT算法,能够有效应对网络中出现的噪声。该文章旨在研究注意力相关的可解释性,利用大量实验来反向验证理论结果。文章利用两种与自监督任务兼容的注意力形式来预测边,边的存在与否都包含了关于节点间关系重要性的内在信息。在实验部分,文章根据基础GAT和SuperGAT构建了四种注意力设计方案,通过实验发现了它们间的区别。此外,还发现了网络的两个特征,即同质性和平均度数,并结合实验给出了指导,在已知这两种网络特征的情况下,应该使用什么样的注意力设计。
1 模型
1.1 定义
文章首先给出了对网络的定义如下:

给出一个网络,通过图注意力层提取节点特征(也可理解为节点嵌入),以上一层的特征为输入,生成的新特征为输出并输入到到下一层。在这个过程中,对节点在某一层的特征h,文章给出了具体的计算方法,通过注意力系数线性结合节点一阶邻居信息,并最终用非线性激活函数完成构建。
1.2 注意力设计方案
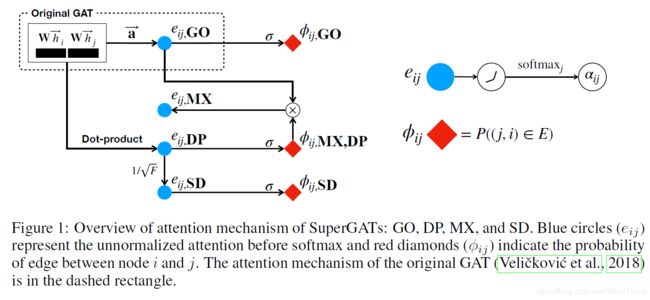
文章结合原始GAT和SuperGAT提出了四种对注意力的设计方案,分别为:GO、DP、SD和MX。
GO指的是原始GAT,即在计算上文提到的注意力系数a时,用参数化的单层前向传播网络计算。而DP指的是点积注意力,即对两个节点的参数化特征做点积。
在此基础上,文章提出了自监督的图注意力网络SuperGAT,关注于节点对中边的出现与否。算法探索了链路预测任务来实验对边上节点标签的自监督,对任意两个节点,都可以计算它们间出现边的概率:
从而,文章进一步介绍了SD(缩放的点积)和MX(混合了GO和DP)。
最终,对单层的目标函数优化如下:
其中,1是一个指示函数,即定义在某集合上的函数,表示其中有哪些元素属于某一子集,在此是为了区分引入了负采样后的损失函数中的正样本和负样本。
这一损失函数是围绕着网络中的边存在与否展开的,此外还有关于节点标签的损失函数,因而算法最终的损失函数形式如下:
2 实验
实验部分,文章提出了四个问题,并围绕这四个问题展开了实验进行验证。这一论述占据较大篇幅,是文章的重心,在此仅简单介绍,不对实验具体内容进行分析。
2.1 注意力学习节点标签一致性吗
结合这一问题,文章设计了相关的验证实验。文章认为,相连接的节点表征在深层GAT中收敛到相同的值,因而如果两个标签不一致的节点间存在边的话,很难用足够多层的GAT来区分这两个标签。换言之,理想的注意力应当把所有的权重都赋予标签一致的邻居,从而能够证明注意力是能够学习到标签一致性的。
因而,文章构建了归一化注意力和标签一致性的分布如下:
并利用KL散度来进行衡量,当注意力很好地捕捉到一个节点与其邻居之间的标签一致时,KL散度的值就会变得很小。
通过实验,文章得到了这样的结果:Does graph attention learn label-agreement? GO learns label-agreement better than DP.
2.2 注意力能预测边是否存在吗
结合这一问题,文章利用链路预测任务展开实验,最终得到结果:Is graph attention predictive for edge presence? DP predicts edge presence better than GO.
文章提出,仅通过优化网络注意力来进行链路预测,很难从边中学习到关系的重要性。
2.3 哪种注意力设计适合运用在网络上
通过实验,文章发现了网络的两种性质:同质性和平均出度,认为使用何种注意力设计要结合具体网络的这两个性质来判断。
同质性指的是网络中噪声的大小,平均出度指的是网络中建立边的频率。其中,同质性的计算方法如下:
在平均出度问题上,文章指出,具有正确标签的数据的绝对数量比噪声和正确标签间的相对比例更能影响学习质量。
这一问题结果是:Which graph attention should we use for given graphs? It depends on homophily and average degree of the graph.
2.4 这种结论对现实数据集有效吗
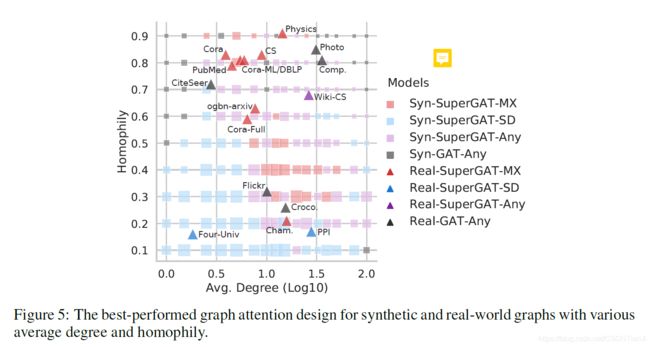
文章为验证上述结论,在17个数据集上进行了实验和对比,根据网络的同质性和平均出度将数据集划分在区间内的不同位置,而不同的注意力设计方法对这些不同的数据集效果不一:
图中,数据集的同质性和平均出度是固定的,而在这些数据集的附近出现算法颜色不同,这就意味着不同属性的数据集其适配的算法类型并不相同。
最终得到的结果是:Does design choice based on RQ3 generalize to real-world datasets? It does for 15 of 17 realworld datasets.