数据挖掘算法原理与实践:k-均值
目录
第一关:什么是质心
任务描述:
相关知识:
什么是质心:
编程要求:
测试说明:
第二关:动手实现k-均值
任务描述:
相关知识:
一、数据集介绍
二、k-means算法原理
三、k-means算法流程
四、如何确定k的值
编程要求:
测试说明:
第一关:什么是质心
任务描述:
本关任务:使用Pyhton编写一个能计算所有样本质心且将所有样本到质心距离按从小到大排序的方法。
相关知识:
为了完成本关任务,你需要掌握:1.什么是质心。
什么是质心:
K-means算法是一个基于距离的聚类方法,距离指的是每个样本到质心的距离。那么,这里所说的质心是什么呢?
其实,质心指的是样本每个特征的均值所构成的一个坐标。举个例子:假如有两个数据(1,1)和(2,2)则这两个样本的质心为(1.5,1.5)。
编程要求:
根据提示,在右侧编辑器Begin-End处补充代码,计算样本间距离distance(x, y, p=2)方法:
x:第一个样本的坐标y:第二个样本的坐标p:等于1时为曼哈顿距离,等于2时为欧氏距离
构造计算所有样本质心的方法cal_Cmass(data):
data:数据样本
与将所有样本到质心距离按从小到大排序的方法sorted_list(data,Cmass):
data:数据样本Cmass:数据样本质心
测试说明:
只需返回预测结果即可,程序内部会检测您的代码,计算正确则视为通过。如:
输入:[[2,3,4],[4,5,6],[5,6,7]] 输出:[0.5773502691896255,2.309401076758503,2.886751345948129]
输入:[[8,8,8],[7,7,7],[9,9,9]] 输出:[0.0, 1.7320508075688772, 1.7320508075688772]
#encoding=utf8
import numpy as np
#计算样本间距离
def distance(x, y, p=2):
'''
input:x(ndarray):第一个样本的坐标
y(ndarray):第二个样本的坐标
p(int):等于1时为曼哈顿距离,等于2时为欧氏距离
output:distance(float):x到y的距离
'''
#********* Begin *********#
dis2 = np.sum(np.abs(x-y)**p)
dis = np.power(dis2,1/p)
return dis
#********* End *********#
#计算质心
def cal_Cmass(data):
'''
input:data(ndarray):数据样本
output:mass(ndarray):数据样本质心
'''
#********* Begin *********#
Cmass = np.mean(data,axis=0)
#********* End *********#
return Cmass
#计算每个样本到质心的距离,并按照从小到大的顺序排列
def sorted_list(data,Cmass):
'''
input:data(ndarray):数据样本
Cmass(ndarray):数据样本质心
output:dis_list(list):排好序的样本到质心距离
'''
#********* Begin *********#
dis_list = []
for i in range(len(data)):
dis_list.append(distance(Cmass,data[i][:]))
dis_list = sorted(dis_list)
#********* End *********#
return dis_list第二关:动手实现k-均值
任务描述:
本关任务:使用python实现kmeans方法,并对鸢尾花数据进行聚类。
相关知识:
为了完成本关任务,你需要掌握:1.k-means算法原理,2.k-means算法流程,3.如何确定k的值。
一、数据集介绍
鸢尾花数据集是一类多重变量分析的数据集,一共有150个样本,通过花萼长度,花萼宽度,花瓣长度,花瓣宽度 4个特征预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
数据集中部分数据如下所示:
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 |
|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 |
| 4.9 | 3.2 | 1.4 | 0.2 |
| 4.7 | 3.1 | 1.3 | 0.2 |
其中每一行代表一个鸢尾花样本各个属性的值。
数据集中部分标签如下图所示:
| 标签 |
|---|
| 0 |
| 1 |
| 2 |
标签中的值0,1,2分别代表鸢尾花三种不同的类别。
我们可以直接使用sklearn直接对数据进行加载,代码如下:
from sklearn.datasets import load_iris
#加载鸢尾花数据集
iris = load_iris()
#获取数据特征与标签
x,y = iris.data.astype(int),iris.target不过为了能够进行可视化我们只使用数据中的两个特征:
from sklearn.datasets import load_irisiris = load_iris()x,y = iris.data,iris.targetx = x[:,2:]
可视化数据分布:
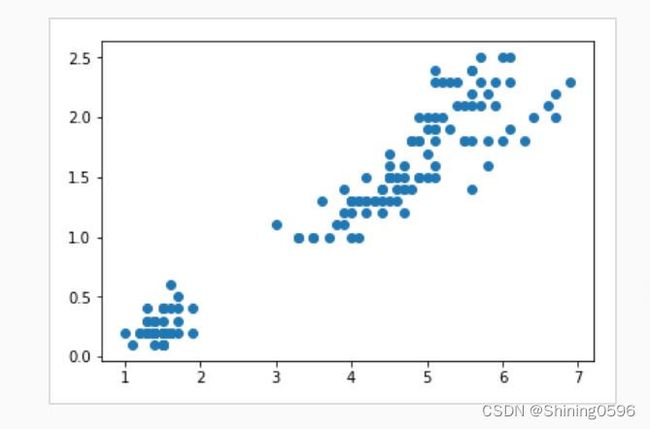
import matplotlib.pyplot as pltplt.scatter(x[:,0],x[:,1])plt.show()
可视化结果:
我们可以先根据数据的真实标签查看数据类别情况:
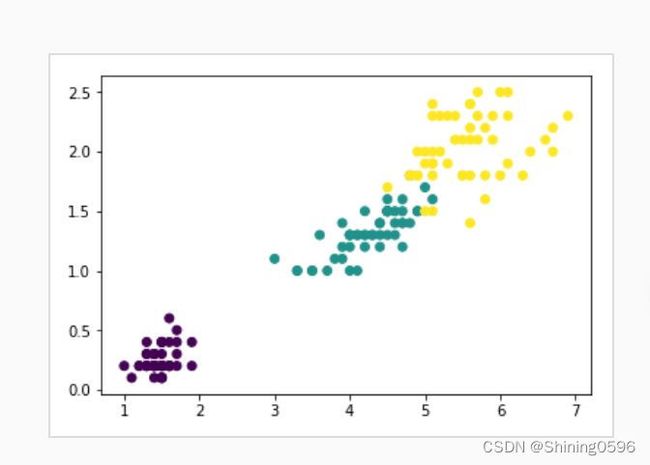
import matplotlib.pyplot as pltplt.scatter(x[:,0],x[:,1],c=y)plt.show()
效果如下:
然后我们划分出训练集与测试集,训练集用来训练模型,测试集用来检测模型性能。代码如下:
from sklearn.model_selection import train_test_split#划分训练集测试集,其中测试集样本数为整个数据集的20%train_feature,test_feature,train_label,test_label = train_test_split(x,y,test_size=0.2,random_state=666)
二、k-means算法原理
K-means算法是基于数据划分的无监督聚类算法,首先定义常数k,常数k表示的是最终的聚类的类别数,在确定了类别数k后,随机初始化k个类别的聚类中心(质心),通过计算每一个样本与聚类中心(质心)的距离,将样本点划分到距离最近的类别中。
三、k-means算法流程
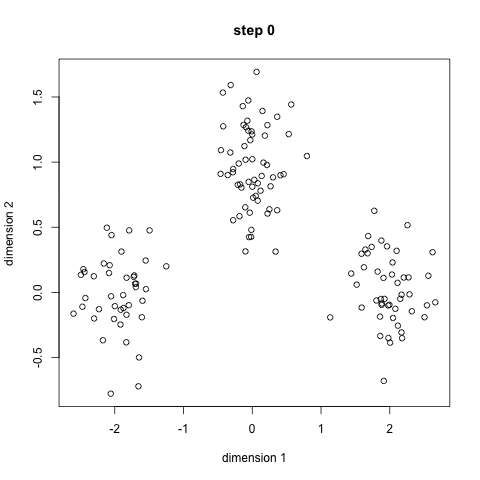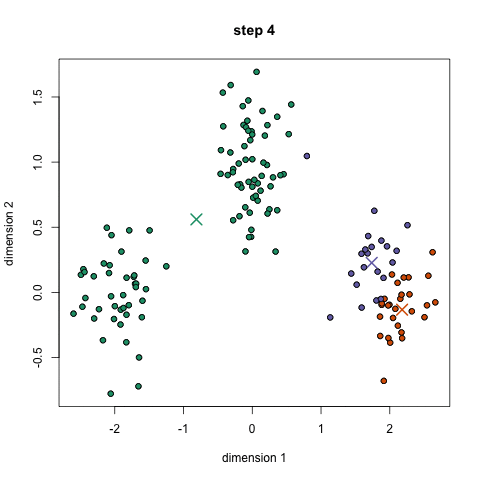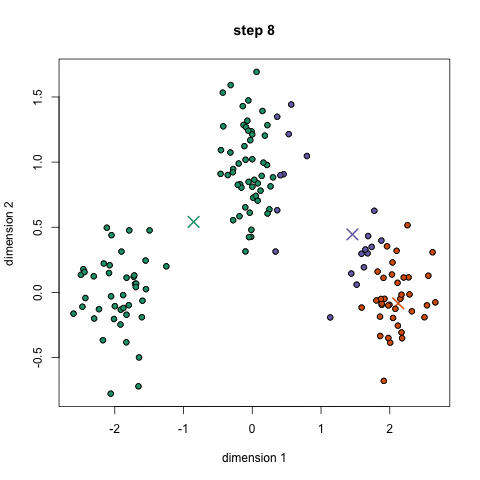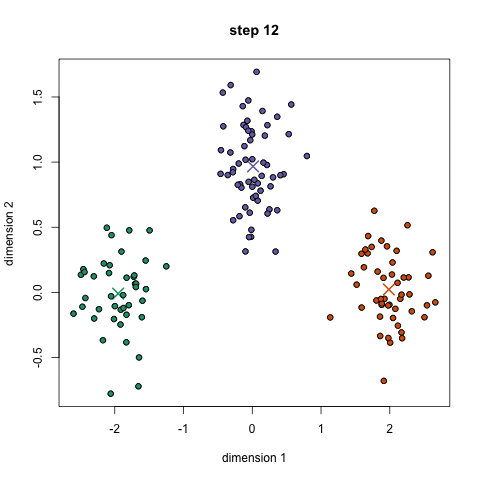
k-means算法流程如下:
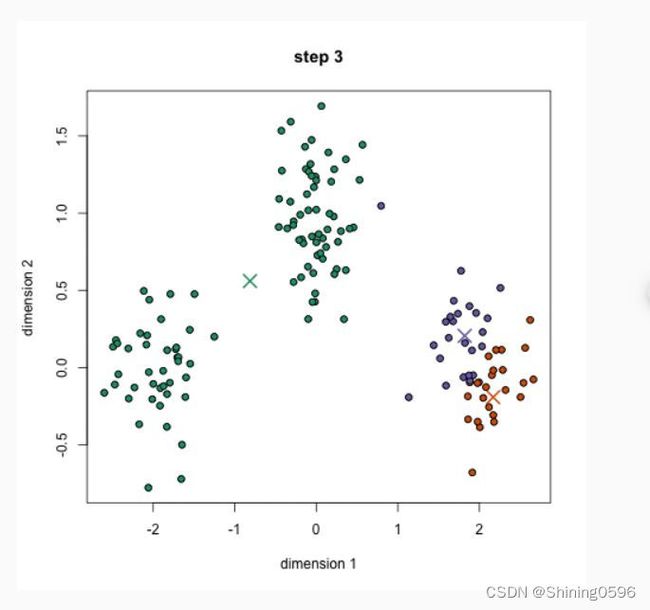
随机初始k个点,作为类别中心。对每个样本将其标记为距离类别中心最近的类别。将每个类别的质心更新为新的类别中心。重复步骤2、3,直到类别中心的变化小于阈值。
过程如下图:
四、如何确定k的值
在K-means算法中,K值作为一个超参数,它的值需要我们自己来确定,通常k默认5。当然我们也可以写一个循环,将k等于各个值的结果输出,选择最好的结果的k值。部分代码如下:
for i in range(k):km = KMmeans(i)
编程要求:
根据提示,在右侧编辑器Begin-End处补充代码,实现kmeans方法,其中距离设为欧氏距离。
测试说明:
程序会调用你实现的方法对鸢尾花数据进行聚类,若聚类结果与正确结果吻合度大于0.95则视为通关。
#encoding=utf8
import numpy as np
# 计算一个样本与数据集中所有样本的欧氏距离的平方
def euclidean_distance(one_sample, X):
'''
input:
one_sample(ndarray):单个样本
X(ndarray):所有样本
output:
distances(ndarray):单个样本到所有样本的欧氏距离平方
'''
#*********Begin*********#
one_sample = one_sample.reshape(1, -1)
distances = np.power(np.tile(one_sample, (X.shape[0], 1)) - X, 2).sum(axis=1)
#*********End*********#
return distances
# 从所有样本中随机选取k个样本作为初始的聚类中心
def init_random_centroids(k,X):
'''
input:
k(int):聚类簇的个数
X(ndarray):所有样本
output:
centroids(ndarray):k个簇的聚类中心
'''
#*********Begin*********#
n_samples, n_features = np.shape(X)
centroids = np.zeros((k, n_features))
for i in range(k):
centroid = X[np.random.choice(range(n_samples))]
centroids[i] = centroid
#*********End*********#
return centroids
# 返回距离该样本最近的一个中心索引
def _closest_centroid(sample, centroids):
'''
input:
sample(ndarray):单个样本
centroids(ndarray):k个簇的聚类中心
output:
closest_i(int):最近中心的索引
'''
#*********Begin*********#
distances = euclidean_distance(sample, centroids)
closest_i = np.argmin(distances)
#*********End*********#
return closest_i
# 将所有样本进行归类,归类规则就是将该样本归类到与其最近的中心
def create_clusters(k,centroids, X):
'''
input:
k(int):聚类簇的个数
centroids(ndarray):k个簇的聚类中心
X(ndarray):所有样本
output:
clusters(list):列表中有k个元素,每个元素保存相同簇的样本的索引
'''
#*********Begin*********#
clusters = [[] for _ in range(k)]
for sample_i, sample in enumerate(X):
centroid_i = _closest_centroid(sample, centroids)
clusters[centroid_i].append(sample_i)
#*********End*********#
return clusters
# 对中心进行更新
def update_centroids(k,clusters, X):
'''
input:
k(int):聚类簇的个数
X(ndarray):所有样本
output:
centroids(ndarray):k个簇的聚类中心
'''
#*********Begin*********#
n_features = np.shape(X)[1]
centroids = np.zeros((k, n_features))
for i, cluster in enumerate(clusters):
centroid = np.mean(X[cluster], axis=0)
centroids[i] = centroid
#*********End*********#
return centroids
# 将所有样本进行归类,其所在的类别的索引就是其类别标签
def get_cluster_labels(clusters, X):
'''
input:
clusters(list):列表中有k个元素,每个元素保存相同簇的样本的索引
X(ndarray):所有样本
output:
y_pred(ndarray):所有样本的类别标签
'''
#*********Begin*********#
y_pred = np.zeros(np.shape(X)[0])
for cluster_i, cluster in enumerate(clusters):
for sample_i in cluster:
y_pred[sample_i] = cluster_i
#*********End*********#
return y_pred
# 对整个数据集X进行Kmeans聚类,返回其聚类的标签
def predict(k,X,max_iterations,varepsilon):
'''
input:
k(int):聚类簇的个数
X(ndarray):所有样本
max_iterations(int):最大训练轮数
varepsilon(float):最小误差阈值
output:
y_pred(ndarray):所有样本的类别标签
'''
#*********Begin*********#
# 从所有样本中随机选取k样本作为初始的聚类中心
centroids = init_random_centroids(k,X)
# 迭代,直到算法收敛(上一次的聚类中心和这一次的聚类中心几乎重合)或者达到最大迭代次数
for _ in range(max_iterations):
# 将所有进行归类,归类规则就是将该样本归类到与其最近的中心
clusters = create_clusters(k,centroids, X)
former_centroids = centroids
# 计算新的聚类中心
centroids = update_centroids(k,clusters, X)
# 如果聚类中心几乎没有变化,说明算法已经收敛,退出迭代
diff = centroids - former_centroids
if diff.any() < varepsilon:
break
y_pred = get_cluster_labels(clusters, X)
#*********End*********#
return y_pred