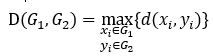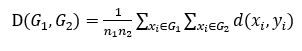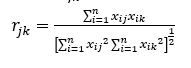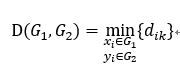常用聚类原理与应用(层次化聚类、k-means、均值漂移聚类)
常用聚类原理与应用
声明:本文章为作者结课拓展小论文,仅供参考,欢迎批评指正。
摘要:
聚类分析是一种对多样本数据进行定量分类的一种多元统计分析方法,是机器学习中无监督学习的典型代表。聚类分析可以根据应用样本的不同上可以分为Q型聚类和R型聚类,其中聚类的标准均来源于样本的属性距离即相似程度。聚类算法常用于机器学习、数据分析等领域中,常用的聚类方法有层次化聚类、k-means聚类、均值漂移聚类,它们各有优劣,算法选择和调参需要参考具体的应用场景。
关键词: 无监督学习、相似度、闵氏距离、k-means聚类
0.引言
当今社会正步入大数据网络时代和智能时代,海量的数据迎面而来,而聚类算法正能够帮助我们从大量的数据中灵活的提取出我们想要获取的有价值的信息特征,无论是机器学习、数据挖掘,聚类算法都是常用的工具。因此,对聚类算法的掌握与应用成为当今社会我们进行数据分析必不可少的工具和助力。本文将围绕聚类算法,主要介绍聚类的概念、分类以及常见的聚类算法和应用。
1. 概念
1.1 定义
聚类分析又称群分析,是对多个样本(或指标)进行定量分类的一种多元统计分析方法。
这里给出Everitt在1974年关于聚类所下的定义:一个类簇内的实体是相似的,不同类簇的实体是不相似的;一个类簇是测试空间中点的会聚,同一类簇的任意两个点间的距离小于不同类簇的任意两个点间的距离;类簇可以描述为一个包含密度相对较高的点集的多维空间中的连通区域,它们借助包含密度相对较低的点集的区域与其他区域(类簇)相分离。
事实上,聚类是一个无监督的分类,它没有任何先验知识可用。
1.2 聚类与分类的区别
Classification(分类),是指按照种类、等级或性质分别归类。分类要求我们提前知道针对数据特征的分类准则、类别,然后对数据集根据掌握的分类标准和数据的特征划分类别。在机器学习中,我们可以给训练数据加标签,划分类别然后学习,最后获取一定的分类能力,然后用于对未知类别数据的分类。这种提供训练数据的学习过程通常被称为supervised learning (有监督学习)。
Clustering(聚类),相对分类而言就是没有提前获取分类的准则和类别,但是要根据数据的特征对没有加标签的数据进行分类的一种行为。因为提前没有获取分类的准则和类别,所以我们既不知道怎么分也不知道分为哪几类,但是要达到分类的目的,所以只能根据变量的相似程度进行分类,具体做法就是把相似的数据分到一类中去。因此聚类的好处是不需要训练数据进行学习,即可划分类别。缺点是由于只能以相似度为准则进行分类,所以不能很好的把握聚类的类别个数,并且聚类结果未必与预期分类结果相符。在机器学习中,这种不提供训练数据即可完成分类的过程被称为unsupervised learning (无监督学习)。
1.3 聚类的流程
1)数据准备:包括特征标准化和降维;
2)特征选择:从最初的特征中选择最有效的特征,并将其存储于向量中;
3)特征提取:通过对所选择的特征进行转换形成新的突出特征;
4)聚类(或分组):首先选择合适特征类型的某种距离函数(或构造新的距离函数)进行接近程度的度量,而后执行聚类或分组;
5)聚类结果评估:是指对聚类结果进行评估,评估主要有3种:外部有效性评估、内部有效性评估和相关性测试评估。
2. 聚类分析的应用类别
2.1分类的标准
聚类分析是对多个样本(或指标)进行定量分类的一种多元统计分析方法。在具体应用场景中我们一般对样本或者指标进行聚类,对样本进行分类称为Q型聚类分析,对指标进行分类称为R型聚类分析。
2.2 Q型聚类
2.2.1样本的相似性度量
要用数量化的方法对样本进行分类,就必须用数量化的方法描述样本之间的相似程度。一个样本本身由多个指标刻画,因此我们通过样本的多个指标来对样本进行分类。每个样本的指标值是不同的,每个样本值都有一定的取值范围,因此我们可以将一个样本的指标值刻画为x、y、z这样的变量,将这个样本刻画为n维(n即指标的数量)空间中的一个点。自然可以想到,我们可以通过空间种样本点与点之间的距离来刻画样本的相似性。
记 Ω 是样本点集,距离d(x,y)是Ω*Ω→R的一个函数,满足条件:
d(x,y)>=0 , x,y∈Ω
d(x,y)=0当且仅当x=y
d(x,y)=d(y,x), x,y∈Ω
d(x,y)<=d(x,z)+d(z,y), x,y,z∈Ω
这是满足正定性、对称性和三角不等式的距离定义。对于距离的度量,最常用的是闵氏(Minkowski)距离,即
![]()
当q=1,2或q→∞,则分别得到:
绝对值距离
![]()
欧几里得(Euclid)距离
![]()
切比雪夫(Chebyshev)距离
![]()
在闵氏距离中,欧几里得距离最常用,它的优点是当坐标轴进行正交旋转时,欧氏距离保持不变。使用闵氏距离需要采用相同的量纲,即需要对数据进行标准化处理。
马氏(Mahalanobis)距离
![]()
马氏距离对一切线性变换是不变的,故不受量纲影响。
2.2.2 类与类的相似性度量
若存在两个样本类G_1和G_2,我们用下面的方法度量它们之间的距离。
最短距离法
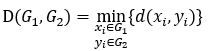
它等于G1和G2中两样本点距离的平均,n1和n2分别为G1和G2中的样本点个数。
离差平方和法
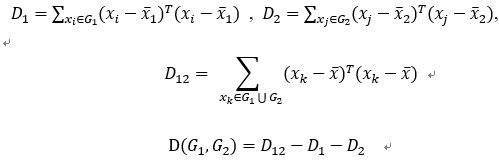
最短距离、最长距离法顾名思义即将两类中样本间的最短/长距离作为两类的距离,重心法是取两类各自物理重心之间的距离作为两类的距离,类平均法是取两类中所有样本之间的距离和的平均值作为类间距离,离差平方和中D_1和D_2分别是两类各自的内部样本之间的距离,D_12则能够刻画两类样本之间的距离,D(G_1,G_2 )=D_12-D_1-D_2 由公式可得两类内部点之间距离越小,两类之间分开距离越大则D值越大,可以看出类差平方和法对聚类中各类的区分更容易达到效果。
2.3 R型聚类
2.3.1变量相似性度量
在聚类的应用中对指标的聚类也十分重要,这种方法可以帮助我们分析各个指标的相关程度,并直观的看出各指标之间的关系,我们可以依据聚类的结果对指标进行筛选,找出最主要的影响因素(指标),剔除相似度高的指标,选取有代表性的指标类别进行下一步的分析预测,这样就节省了大量的时间,避免了重复的工作。因此指标(变量)的相似度作为区分各类的重要指标,相似度越高,越容易被聚为一类。以下为几种有代表性的相似度度量方式。
相关系数
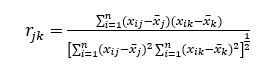
可以利用两变量xj与xk的夹角余弦 rjk来定义它们的相似性度量。
2.3.2变量聚类
类似于样本集合聚类分析的类距离计算方法,指标(变量)聚类也可以采取最长距离法、最短距离法等。
最长距离法
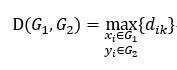
其中d_ik=1-|r_jk |或d_jk2=1-r_jk2。
3.常用聚类算法
3.1层次化聚类
此处介绍采取自下而上策略的凝聚型层次聚类(AGENES),以Q型聚类为例,我们先对样本进行预处理,将样本抽象为在一个k维的空间里的n个点,n个点为n个不同的样本,样本的指标数为k。我们选取相应的距离计算公式,首先计算每个点与其他所有不同点的距离。然后选取这些距离中的最短距离,并把最短距离连接的两个样本归为一类,并将其此两样本间的距离作为聚类图中这两个样本的共同平台高度。然后选取类间距离的计算方式,并重新计算此类与其他样本之间的距离,计算后回到第一步,选取所有样本类别距离的最小值,合并并设置平台高度,重新计算距离,往复直至所有的样本聚为一类。
输出为聚类图,我们可以分析聚类图,根据聚类图的各类平台间的高低选择聚类类别的数量,平台高度差越大即两类差距越大,在聚类图中选取一个固定的平台高度即可完成对聚类类别的选取,如图所示:
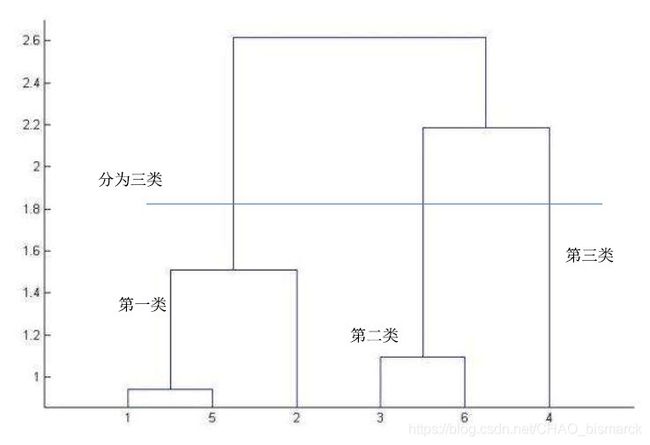
图1. 层次化聚类图
严格程序步骤如下:设Ω={w1, w2, w3,…,wn}

显而易见,这种聚类方法的结果与选取的样本和类之间的距离公式以及选取的类的数量有关。此处描述的层次聚类方法主要是自下而上的聚类,一开始假设所有样本各为一类,然后合并最相似的样本并不断迭代,最终所有样本聚为一类。这种方法可以直观简单的对具有多个指标的样本或者多个指标(变量)进行聚类,并在画出聚类图后根据聚类图和样本信息自主的选择聚类的个数,是一种简单易行的聚类方法。
这种聚类方法适合处理未知聚类个数且含有多指标的样本聚类问题,如要求对样本聚类,根据售货员的多个销售业绩指标为售货员划分等级,可以使用层次化Q型聚类,要求对指标聚类,通过分析各个地区的多个教育水平指标数据,选出最有代表性的几个指标,可以使用层次化R型聚类。层次分析法的算法复杂度为O(n^3),因此不适合大量数据的处理,数据越多算法所需时间越长,数据较多时可以采用k-means聚类算法。
3.2 k-means聚类
k-means聚类是一种典型的基于距离进行聚类的聚类方法。首先构造样本空间,选取k个样本点,并将这k个点作为k个类的聚类中心,计算其他样本到这k个聚类中心的距离,将其他的点分别划分到距离最近的聚类中心所在的类里去。然后,重新计算k个类的中心点,重新计算所有样本到k个聚类中心的距离,重新划分所有样本。往复迭代直到满足某个终止条件,迭代停止,聚类完成。终止条件可以是以下三种:
(1)没有样本点被重新分配给不同的类
(2)聚类中心不再改变
(3)误差平方和局部最小
K-means算法步骤:

k-means算法是典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个样本的距离越近,其相似度就越大。这种算法以得到紧凑且独立的类别作为最终目标。
输出聚类图如下:
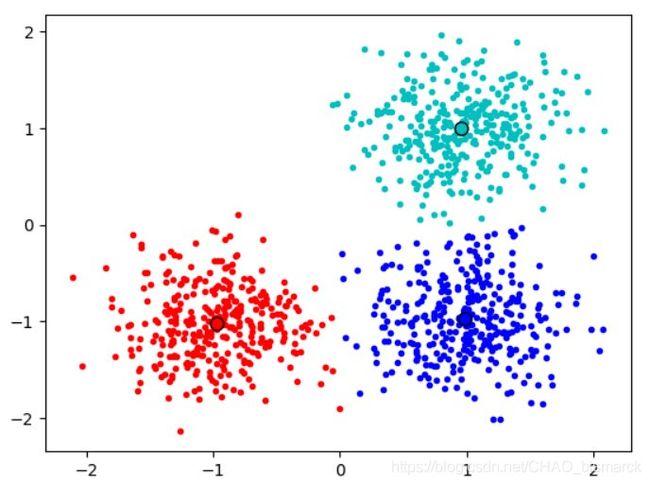
图2. k-means聚类结果图(图片引用,侵权必删)
k-means算法在计算前需要提前设定k值即聚类结果中类别的个数,因此需要专门的方法确定最适合的k值才能使k-means算法达到最佳效果。一个简单、快速的计算方法是将样本数除2开放得出的值作为k值。对于容易观察的数据(如二维数据),我们可以通过观察发现主要的类别个数,从而找到适合的k值。对于不容易观察的数据,如果数据的数量有限,我们可以设置误差平方和,多试几个不同的k值,最后选取最小误差的k值即为合适的k值。若数据量比较大或要求比较严格,我们可以采用肘部法则(Elbow Method)来确定k值。
手肘法则指计算误差平法和公式f(x)=SSE(x),k与SSE存在某种关系,当x
SSE(sum of the squared erroes)误差平法和计算公式如下:
![]()
p 为样本点位置,m_i为每个类的聚类中心点位置,c_j为每个类。
k-means算法的时间复杂度为o(IKN),其中N为样本点个数,K为中心点个数,I为迭代次数。k-means算法的优点是运算速度快、简单,聚类效果较好,适用于高维,缺点是对离群点敏感,对噪声点和孤立点很敏感,聚类个数k需要提前设定,初始聚类中心的选择,不同的初始点选择可能导致完全不同的聚类结果。
3.3均值漂移聚类
均值漂移聚类是一种基于滑动窗口的均值算法,算法不断寻找样本数据点中密度最大的区域。该方法的二维表述比较形象,首先将数据点置于二维平面中,在空间中随机选取一定数量的点,以这些点为圆心,选取定值为半径画一个圆形窗口,计算出该窗口内数据点密度最大的点,用密度最大的点替换之前的点,然后以替换后的密度最大的点为圆心,定值为半径继续画圆形窗口,重复迭代。这样窗口会不断向数据点密集的位置移动,直到到达数据点最密集的位置,当窗口重叠或者所有窗口不再移动时算法结束,即可完成聚类,窗口中心点即为聚类中心点。该算法显然使用了爬山法的思想,使窗口中心不断向数据点密度高的地方移动,最终达到聚类的目的。
具体步骤如下:

相对于k-means算法来讲,该方法不需要提前指定聚类数目,聚类数目自行确定,且相对来说比较符合直观认知的结果。缺点是滑动窗口半径的选取,对聚类的结果有很大影响,在样本含多属性的情况下,使用该方法应对指标值进行适当的量纲预处理,使其适应选取的窗口半径。
4.聚类的应用
在商业领域,聚类分析可以针对目标群体进行多指标的群体划分,通过分类辨认有典型特征的类别,从而制定相应的商业策略,进行个性化和精细化的运营,服务及产品支持等;在数据分析中我们还可以通过聚类发现异常点、异常数据,进行针对处理;在社会调查上,我们可以通过聚类对搜集到的大量数据进行分析,从而区分好坏、高低,建立一套评价体系;对于多指标的大量数据,我们在调查分析前可以通过聚类选取出最有代表性的指标进行分析,节省大量和精力和资源;聚类的应用用途还有很多,现今我们正步入网络信息时代,大数据爆炸比比皆是,而聚类分析是大数据分析、数据挖掘、机器学习的重要工具。
5.结语
论文第一部分主要讨论的聚类算法的基本概念、与分类的区别以及基本流程和评价标准,理解好聚类的概念,聚类与分类的区别,才能更清楚的明白聚类的用途和原理。论文第二节讨论了聚类的分类,主要分为Q型聚类和R型聚类,并且介绍了聚类中样本点距离计算的多个公式,熟悉聚类的分类和距离计算公式帮助我们用好聚类,通过分析应用场景选择适合的算法类别和距离公式将有助于我们更好的聚类分析。论文的最后主要介绍了三种常用的聚类算法,分别是层次法、k-means聚类、均值漂移聚类,其中k-means聚类应用较多,我们对k值的选取也提供了多种参考方法。总之,本文介绍了聚类算法基础的概念、分类以及一些常用聚类算法如k-means算法的原理和步骤。
参考文献:
[1]李玲玲,关于凝聚型层次聚类时间复杂度的研究,宿州学院学报.Vol. 26, No. 2,2011:21-22,
[2]司守奎,孙兆亮,数学建模算法与应用(第二版)
[3]MATLAB数学建模方法与实践(第三版)
[4]数据科学中必须熟知的五种聚类算法:
https://baijiahao.baidu.com/s?id=1625408992304959354&wfr=spider&for=pc
[5]聚类的概念、过程与算法:http://blog.sina.com.cn/s/blog_78bdf8e801013wx6.html
[6]机器学习之k-means算法详解:
https://blog.csdn.net/sinat_30353259/article/details/80887779?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-10&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-10
[7]k-means算法之k值的选择:https://www.biaodianfu.com/k-means-choose-k.html
[8]聚类分析典型应用: https://www.jianshu.com/p/7b13610eb674