【贝叶斯分类3】半朴素贝叶斯分类器

1. 朴素贝叶斯分类器知识回顾

1.1 类别，特征

  我们根据贝叶斯决策论，或者说是贝叶斯分类原理，首先得到的是一个期望损失【$R(c_i|x)={\sum }_{j=1}^N{\lambda }_{ij}P(c_j|x)$】。贝叶斯判定准则就是要让总体风险最小，从而可推到要求部分风险最小【$h^{\ast }(x)=argmi{n}_{c\in Y}R(c|x)$】。
  可以把$c$ 看作“类别”，把$x$ 看作“特征”。$R(c|x)$ 就是一种类别，它有自己的特征，如【好瓜：色泽=青绿，纹理=清晰，…，密度 $\ge$ 0.697】，$c=\{好瓜，坏瓜\}$，$x=\{青绿，清晰，...，密度\}$，我们根据特征算类别（正确与否）的风险，风险越小，代表类别越正确。

1.2 风险，概率

  根据误判损失，我们进一步推导出$R(c_{|}x)=1-P(c|x)$，$P(c|x)=P(类别|特征)$ 可以理解为：这个类别，通过这些特征，出现的（或者讲事件发生的概率）概率。例如：【好瓜：色泽=青绿，纹理=清晰，…，密度 $\ge$ 0.697】，我们就说：【色泽=青绿，纹理=清晰，…，密度 $\ge$ 0.697】就是好瓜（概率很大）。所以这就是根据特征，不断调整类别的概率，是后验概率。
  我们自然希望，根据这些特征推出来是好瓜的概率越大越好，所以有：【$h^{\ast }(x)=argma{x}_{c\in Y}P(c|x)$，数据集有几个类别，一个样本就有几个$P(c|x)$，我们根据这几个$P(c|x)$的大小，选择值最大的，那么这个样本就被划分为这一类。】。我们要求$P(c|x)$ 这个概率，有公式：【$P(c|x)=\frac{P(c)P(x|c)}{P(x)}$】，它是所有属性的联合概率（实际中，会遇到：组合爆炸，缺少值等），难点在求类条件概率$P(x|c)$。我们朴素贝叶斯为了解决后验概率（$P(c|x)$）不好算的问题，提出了【属性条件独立性假设】（属性也可以叫特征）。

1.3 类条件概率

  朴素贝叶斯分类器的表达式：【$h_{nb}(x)=argma{x}_{c\in Y}P(c){\prod }_{i=1}^{d}P(x_i|c)$】，重点在求类条件概率上，基本上我们以数据集计算过程中都用的是“缩减样本空间法”，而没有用概率论上的一些条件概率的计算公式。简单来说，就是统计样本个数，再做比例运算。

2. 半朴素贝叶斯分类器学习笔记

2.1 引言

  朴素贝叶斯分类器采用“属性独立性假设”，现实任务中很难成立。于是，人们尝试对属性条件独立性假设进行一定程度的放松，由此产生了一类称为"半朴素贝叶斯分类器" (semi-naïve Bayes classifiers) 的学习方法。基本思想：【适当考虑一部分属性间的相互依赖信息】。

2.2 知识卡片

	1. 半朴素贝叶斯分类器：semi-naive Bayes classifiers
	2. 又叫：SNB算法

2.3 半朴素贝叶斯分类器

• 半朴素贝叶斯分类器的表达式

$p{a}_i$ 是属性$x_j$ 所依赖的属性，称为$x_j$ 的父属性
$$P(c|x)\propto P(c)\prod _{j=1}^{d}P(x_j|c,p{a}_i)$$

• 独依赖分类器

  问题的关键就转化为如何确定每个属性的父属性，不同的做法产生不同的独依赖分类器。

2.4 独依赖估计

2.4.1 简介

- "英文："
	One-Dependent Estimator，简称：ODE

- "用途："
	它是半朴素贝叶斯分类器，适当考虑一部分属性间的相互依赖信息，最常采用的一种策略。

- "ODE原理："
	假设每个属性在类别之外最多仅依赖于一个其他属性

- "适当考虑一部分属性间的相互依赖信息:"
	考虑策略不同，形成的独依赖分类器也不同。代表：
	1）SPODE（Super-Parent ODE）
	2）TAN（Tree Augmented naive Bayes）
	3）AODE（Average ODE）

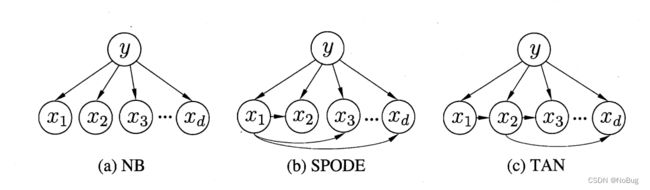
2.4.2 SPODE(超父独依赖估计)

• 原理

  所用特征都依赖唯一的一个特征，这个被依赖的特征就叫做超父（super-parent）。然后通过交叉验证确定超父（分别假设每个属性都是超父时，选择效果最好的）。

• 图1

• 例子

【数据集】

$x_1$	$x_2$	$x_3$	$y$
1	1	1	1
1	0	0	1
1	1	1	1
1	0	0	0
1	1	1	0
0	0	0	0
0	1	1	0
0	1	0	1
0	1	1	0
0	0	0	0

【预测】

$x_1$	$x_2$	$x_3$	$y$
1	1	0	?

【SPODE公式】

$$P(c|x)\propto argma{x}_{c\in Y}P(c)\prod _{j=1}^{d}P(x_j|c,p{a}_i)$$

【先验概率$P(c)$】
$$P(y=1)=\frac{4}{10}=0.4$$

$$P(y=0)=\frac{6}{10}=0.6$$

【类条件概率$P(x_i|c,p{a}_i)$[先假定$x_1$ 为超父$p{a}_i=x_1$]】
$$P(x_1=1|y=1)=\frac{3}{4}$$

$$P(x_2=1|y=1,x_1=1)=\frac{2}{3}$$

$$P(x_3=0|y=1,x_1=1)=\frac{1}{3}$$

$$P(x_1=1|y=0)=\frac{2}{6}=\frac{1}{3}$$

$$P(x_2=1|y=0,x_1=1)=\frac{1}{2}$$

$$P(x_3=0|y=0,x_1=1)=\frac{1}{2}$$

【半朴素贝叶斯分类器】
$$P(y=1)=0.4\ast 0.75\ast \frac{2}{3}\ast \frac{1}{3}=0.067$$

$$P(y=1)=0.6\ast \frac{1}{3}\ast \frac{1}{2}\ast \frac{1}{2}=0.050$$

$$所以，预测样本类别，y=1$$

2.4.3 AODE(平均独依赖估计)

• 原理

  SPODE是选择一个模型进行预测，AODE是一种基于集成学习机制的独依赖分类器。在AODE中，每个模型进行一次预测，然后将结果平均后得到最终的预测结果。(AODE 尝试将每个属性作为超父来构建 SPODE，然后即将那些具有足够训练数据支撑的 SPODE 集成起来作为最终结果。)

• 理解公式

$$P(c|x)\propto \frac{{\sum }_{i=1}^{d}P(c,x_i){\prod }_{j=1}^{d}P(x_j|c,x_i)}{d}$$

• 阈值$m^{\prime }$

  例如上面例题中，$P(x_2=1|y=0,x_1=1)=\frac{1}{2}$，有可能分母为1，导致可用样本数量太少了。于是，AODE加入一个阈值，要求超父特征为某一特定值的样本的数量大于等于 m’ 时，才可使用这个 SPODE 模型。

• AODE公式

$$P(c|x)\propto \sum _{i=1}^{d}P(c,x_i)\prod _{j=1}^{d}P(x_j|c,x_i),|D_{x_i}|\ge m^{\prime }$$

• 参数求解

【$P(c,x_i)$】

$$P(c,x_i)=\frac{|D_{c,x_i}|+1}{|D|+N_i}$$

【$P(x_j|c,x_i)$】
$$P(x_j|c,x_i)=\frac{|D_{c,x_i,x_j}|+1}{|D_{c,x_i}|+N_j}$$

2.4.4 TAN(树增广朴素贝叶斯)

• 引言

  不管是SPODE，还是AOED，尽管超父在变换，但每个模型中每个特征都依赖于超父特征。现实情况中，特征的依赖情况也不大可能都依赖于其中之一，而是可能每个特征的依赖都不一样。TAN 可以解决这个问题，找到每个特征最适合依赖的另外一个特征。

• 原理

  在最大带权生成树算法基础上构建依赖。TAN 计算两两特征之间的条件互信息，在选择每个特征的依赖特征时，选择互信息最大的对应特征即可（条件互信息的值即代表了两个特征之间互相依赖的程度）。

• 算法

3. 半朴素贝叶斯分类器拓展

3.1 kDE(k依赖估计)

  既然将属性条件独立性假设放松为独依赖假设可能获得泛化性能的提升，那么，能否通过考虑属性间的高阶依赖（对多个属性依赖）来进一步提升泛化性能呢？相当于，将 ODE 拓展为kDE。若训练数据非常充分，可以考虑。