深度学习之循环神经网络(6)梯度弥散和梯度爆炸
深度学习之循环神经网络(6)梯度弥散和梯度爆炸
循环神经网络的训练并不稳定,网络的善妒也不能任意加深。那么,为什么循环神经网络会出现训练困难的问题呢?简单回顾梯度推导中的关键表达式:
∂ h t ∂ h i = ∏ j = 1 t − 1 d i a g ( σ ′ ( W x h x j + 1 + W h h h j + b ) ) W h h \frac{∂\boldsymbol h_t}{∂\boldsymbol h_i}=\prod_{j=1}^{t-1}diag(σ'(\boldsymbol W_{xh} \boldsymbol x_{j+1}+\boldsymbol W_{hh} \boldsymbol h_j+\boldsymbol b))\boldsymbol W_{hh} ∂hi∂ht=j=1∏t−1diag(σ′(Wxhxj+1+Whhhj+b))Whh
也就是说,从时间戳 i i i到时间戳 t t t的梯度 ∂ h t ∂ h i \frac{∂\boldsymbol h_t}{∂\boldsymbol h_i} ∂hi∂ht包含了 W h h \boldsymbol W_{hh} Whh的连乘运算。当 W h h \boldsymbol W_{hh} Whh的 最大特征值(Largest Eignvalue)小于1时,多次连乘运算会使得 ∂ h t ∂ h i \frac{∂\boldsymbol h_t}{∂\boldsymbol h_i} ∂hi∂ht的元素值接近于0;当 W h h \boldsymbol W_{hh} Whh的最大特征值大于1时,多次连乘运算会使得 ∂ h t ∂ h i \frac{∂\boldsymbol h_t}{∂\boldsymbol h_i} ∂hi∂ht的元素值爆炸式增长。
我们可以从下面的两个例子直观地感受一下梯度弥散和梯度爆炸现象的产生,代码如下:
import tensorflow as tf
W = tf.ones([2, 2]) # 任意创建某矩阵
eigenvalues = tf.linalg.eigh(W)[0] # 计算矩阵的特征值
print(eigenvalues)
运行结果如下所示:
tf.Tensor([0. 1.9999999], shape=(2,), dtype=float32)
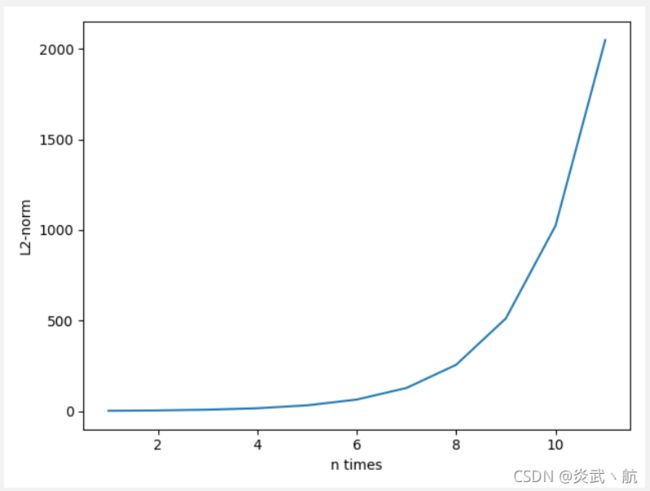
可以看到,全1矩阵的最大特征值为2。计算 W \boldsymbol W W矩阵的 W 1 ∼ W 10 \boldsymbol W^1\sim \boldsymbol W^{10} W1∼W10运算结果,并绘制为次方与矩阵的L2-范数的曲线图:
val = [W]
for i in range(10): # 矩阵相乘n次方
val.append([val[-1]@W])
# 计算L2范数
norm = list(map(lambda x: tf.norm(x).numpy(), val))
print(norm)
plt.plot(range(1, 12), norm)
plt.xlabel('n times')
plt.ylabel('L2-norm')
plt.savefig('w_n_times_1.svg')
plt.show()
运行结果如下:
[2.0, 4.0, 8.0, 16.0, 32.0, 64.0, 128.0, 256.0, 512.0, 1024.0, 2048.0]
可以看到,当 W \boldsymbol W W矩阵的最大特征值大于1时,矩阵多次相乘会使得结果越来越大。
考虑最大特征值小于1的情况。例如:
import tensorflow as tf
W = tf.ones([2, 2])*0.4 # 任意创建某矩阵
eigenvalues = tf.linalg.eigh(W)[0] # 计算矩阵的特征值
print(eigenvalues)
运行结果如下所示:
tf.Tensor([0. 0.79999995], shape=(2,), dtype=float32)
可以看到此时的 W \boldsymbol W W矩阵最大特征值是0.8。同样的方法,考虑 W \boldsymbol W W矩阵的多次相乘运算结果,代码如下:
val = [W]
for i in range(10): # 矩阵相乘n次方
val.append([val[-1]@W])
# 计算L2范数
norm = list(map(lambda x: tf.norm(x).numpy(), val))
print(norm)
plt.plot(range(1, 12), norm)
plt.xlabel('n times')
plt.ylabel('L2-norm')
plt.savefig('w_n_times_0.svg')
plt.show()
运行结果如下所示:
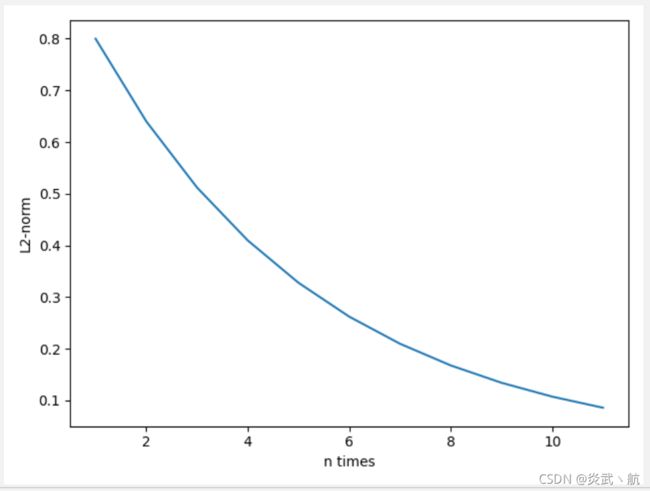
[0.8, 0.64000005, 0.512, 0.40960002, 0.32768002, 0.26214403, 0.20971523, 0.16777219, 0.13421775, 0.107374206, 0.08589937]
它的L2-范数曲线如上图所示。可以看到,当 W \boldsymbol W W矩阵的最大特征值小于1时,矩阵多次相乘会使得结果越来越小,接近于0。
注:特征值的作用和意义体现在用矩阵进行列向量的高次变换也就是矩阵的高次方乘以列向量的计算中。数学中的很多变换可以用矩阵的乘法来表示,在这样的变换中,一个列向量(点) α α α变成另一个列向量(点) β β β的过程可以看成是一个矩阵 A \boldsymbol A A乘以 α α α得到 β β β,即 A α = β \boldsymbol Aα=β Aα=β,如果把同样的变换连续的重复的做 n n n次则需要用矩阵高次方来计算: A n ⋅ α \boldsymbol A^n\cdotα An⋅α,如果没有特征值和特征向量,此处就要计算矩阵 A \boldsymbol A A的 n n n次方,这个运算量随着 n n n的增加,变得越来越大,很不方便。而利用特征值和特征向量,可以达到简化计算的目的。
参考:什么是最大特征值
我们把梯度值接近于0的现象叫做梯度弥散(Gradient Vanishing),把梯度值远大于1的现象叫做梯度爆炸(Gradient Exploding)。梯度弥散和梯度爆炸是神经网络优化过程中间比较容易出现的两种情况,也是不利于网络训练的。那么梯度弥散和梯度爆炸具体表现在哪些地方呢?
考虑梯度下降算法:
θ ′ = θ − η ∇ θ L θ'=θ-η∇_θ \mathcal L θ′=θ−η∇θL
当出现梯度弥散时, ∇ θ L ≈ 0 ∇_θ \mathcal L≈0 ∇θL≈0,此时 θ ′ ≈ θ θ'≈θ θ′≈θ,也就是说每次梯度更新后参数基本保持不变,神经网络的参数长时间得不到更新,具体表现为 L \mathcal L L几乎保持不变,其他评测指标,如准确度,也保持不变。当出现梯度爆炸时, ∇ θ L ≫ 1 ∇_θ \mathcal L≫1 ∇θL≫1,此时梯度的更新步长 η ∇ θ L η∇_θ\mathcal L η∇θL非常大,使得更新后的 θ ′ θ' θ′与 θ θ θ差距很大,网络L出现突变现象,甚至可能出现来回震荡、不收敛的现象。
通过推导循环神经网络的梯度传播公式,我们发现循环神经网络很容易出现梯度弥散和梯度爆炸的现象。那么怎么解决这两个问题呢?——梯度裁剪。