深度学习之循环神经网络(7)梯度裁剪
深度学习之循环神经网络(7)梯度裁剪
- 1. 张量限幅
- 2. 限制范数
- 3. 全局范数裁剪
- 梯度弥散
梯度爆炸可以通过 梯度裁剪(Gradient Clipping)的方式在一定程度上的解决。梯度裁剪与张量限幅非常类似,也是通过将梯度张量的数值或者范数限制在某个较小的区间内,从而将远大于1的梯度值减少,避免出现梯度爆炸。
在深度学习中,有3种常用的梯度裁剪方式。
1. 张量限幅
直接对张量的数值进行限幅,使得张量 W \boldsymbol W W的所有元素 w i j ∈ [ min , max ] w_{ij}\in[\text{min},\text{max}] wij∈[min,max]。在TensorFlow中,可以通过tf.clip_by_value()函数来实现。例如:
import tensorflow as tf
a = tf.random.uniform([2, 2])
# print(a)
print(tf.clip_by_value(a, 0.2, 0.6)) # 梯度值裁剪
运行结果如下所示:
tf.Tensor(
[[0.46144927 0.6 ]
[0.4977187 0.22363663]], shape=(2, 2), dtype=float32)
2. 限制范数
通过限制梯度张量 W \boldsymbol W W的范数来实现梯度裁剪。比如对 W \boldsymbol W W的二范数 ∥ W ∥ 2 \|\boldsymbol W\|_2 ∥W∥2约束在 [ 0 , max ] [0,\text{max}] [0,max]之间,如果 ∥ W ∥ 2 \|\boldsymbol W\|_2 ∥W∥2大于 max \text{max} max值,则按照
W ′ = W ∥ W ∥ 2 ⋅ max \boldsymbol W'=\frac{\boldsymbol W}{\|\boldsymbol W\|_2} \cdot \text{max} W′=∥W∥2W⋅max
方式将 ∥ W ∥ 2 \|\boldsymbol W\|_2 ∥W∥2约束在 max \text{max} max内。可以通过tf.clip_by_norm函数方便地实现梯度张量 W \boldsymbol W W裁剪。例如:
import tensorflow as tf
a = tf.random.uniform([2, 2]) * 5
# 按范数方式裁剪
b = tf.clip_by_norm(a, 5)
# 裁剪前和裁剪后的张量范数
print(tf.norm(a), tf.norm(b))
运行结果如下所示:
tf.Tensor(6.1878695, shape=(), dtype=float32) tf.Tensor(5.0, shape=(), dtype=float32)
可以看到,对于大于 max \text{max} max的L2范数的张量,通过裁剪后范数值缩减为5。
3. 全局范数裁剪
神经网络的更新方向是由所有参数的梯度张量 W \boldsymbol W W共同表示的,前两种方式只考虑单个梯度张量的限幅,会出现网络更新方向发生变动的情况。如果能够考虑所有参数的梯度 W \boldsymbol W W的范数,实现等比例的缩放,那么就能既很好地限制网络的梯度值,同时不改变网络的更新方向。这就是第三种梯度裁剪的方式:全局范数裁剪。在TensorFlow中,可以通过tf.clip_by_global_norm函数快捷地缩放整体网络梯度 W \boldsymbol W W的范数。
令 W ( i ) \boldsymbol W^{(i)} W(i)的表示网络参数的第 i i i个梯度张量,首先通过
global_norm = ∑ i ∥ W ( i ) ∥ 2 2 \text{global\_norm}=\sqrt{\sum_i\|\boldsymbol W^{(i)} \|_2^2 } global_norm=i∑∥W(i)∥22
计算网络的总范数 global_norm \text{global\_norm} global_norm,对第 I I I个参数 W ( i ) \boldsymbol W^{(i)} W(i),通过
W ( i ) = W ( i ) ⋅ max_norm max(global_norm,max_norm) \boldsymbol W^{(i)}=\frac{\boldsymbol W^{(i)}\cdot \text{max\_norm}}{\text{max(global\_norm,max\_norm)}} W(i)=max(global_norm,max_norm)W(i)⋅max_norm
进行裁剪,其中 max_norm \text{max\_norm} max_norm是用户指定的全局最大范数值。例如:
import tensorflow as tf
w1 = tf.random.normal([3,3]) # 创建梯度张量1
w2 = tf.random.normal([3,3]) # 创建梯度张量2
# 计算global norm
global_norm = tf.math.sqrt(tf.norm(w1)**2+tf.norm(w2)**2)
# 根据global norm和max norm=2裁剪
(ww1, ww2), global_norm = tf.clip_by_global_norm([w1,w2],2)
# 计算裁剪后的张量组的global norm
global_norm2 = tf.math.sqrt(tf.norm(ww1)**2+tf.norm(ww2)**2)
print(global_norm, global_norm2)
运行结果如下所示:
tf.Tensor(4.220784, shape=(), dtype=float32) tf.Tensor(1.9999999, shape=(), dtype=float32)
可以看到,通过裁剪后,网络参数的梯度组的总范数缩减到 max_norm = 2 \text{max\_norm}=2 max_norm=2。需要注意的是,tf.clip_by_global_norm返回裁剪后的张量List和global_norm这两个对象,其中global_norm表示裁剪前的梯度总范数和。
通过梯度裁剪,可以较大程度地抑制梯度爆炸现象。如下图所示,图中曲面表示的 J ( w , b ) J(w,b) J(w,b)函数在不同网络参数 w w w和 b b b下的误差值 J J J,其中有一块区域 J ( w , b ) J(w,b) J(w,b)函数的梯度变化较大,一旦网络参数进入此区域,很容易出现梯度爆炸的现象,使得网络状态迅速恶化。下图右侧演示了添加梯度裁剪后的优化轨迹,由于对梯度进行了有效限制,使得每次更新的步长得到有效控制,从而防止网络突然恶化。
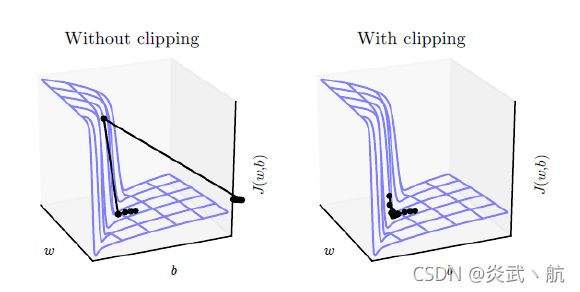
在网络训练时,梯度裁剪一般在计算出梯度后,梯度更新之前进行。例如:
with tf.GradientTape() as tape:
logits = model(x) # 前向传播
loss = criteon(y, logits) # 误差计算
# 计算梯度值
grads = tape.gradient(loss, model.trainable_variables)
grads, _ = tf.clip_by_global_norm(grads, 25) # 全局梯度裁剪
# 利用裁剪后的梯度张量更新参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))
梯度弥散
对于梯度弥散现象,可以通过增大学习率、减少网络深度、增加Skip Connection等一系列的措施抑制。
增大学习率 η η η可以在一定程度上防止梯度弥散现象,当出现梯度弥散时,网络的梯度 ∇ θ L ∇_θ\mathcal L ∇θL接近于0,此时若学习率 η η η也较小,如 η = 1 e − 5 η=1\text{e}-5 η=1e−5,则梯度更新步长更加微小。通过增大学习率,如令 η = 1 e − 2 η=1\text{e}-2 η=1e−2,有可能使得网络的状态得到快速更新,从而逃离梯度弥散区域。
对于深层次的神经网络,梯度由最末层逐渐向首层传播,梯度弥散一般更有可能出现在网络的开始数层。在深度残差网络出现之前,几十上百层的深层网络训练起来非常困难,前面数层的物流梯度极容易出现梯度离散现象,从而使得网络参数长时间得不到更新。深度残差网络较好地克服了梯度弥散现象,从而让神经网络层数达到成百上千层。一般来说,减少网络深度可以减轻梯度弥散现象,但是网络层数减少后,网络表达能力也会偏弱,需要用户自行平衡。