偏最小二乘法的几种解释
文章目录
- 前面的文章
- 基础准备
-
- 最小二乘法的几何意义
- 典型相关分析
- 主成分分析
- 第一种解释
- 第二种解释
- 第三种解释
- 第四种解释
- 总结
- 参考文献
经过一段时间的学习,对偏最小二乘法有了一些了解,这里做一个总结。下面主要是针对PLS1,也就是单响应变量的情况
前面的文章
- 偏最小二乘法(NIPALS经典实现–未简化)
- 偏最小二乘法 基本性质推导
- 偏最小二乘法(SIMPLS—未简化)
- 偏最小二乘法PLS(matlab自带代码)
- PLSR的扩展性质
- PLS中的权值和载荷
- OLS,PCA,CCA,PLS和CR的关系总结及几何解释
基础准备
最小二乘法的几何意义
y = X β = β 1 x 1 + ⋯ + β n x n (1) \mathbf{y} = X\mathbf{\beta} = \beta_1\mathbf{x_1}+\dots+\beta_n\mathbf{x_n} \tag{1} y=Xβ=β1x1+⋯+βnxn(1)
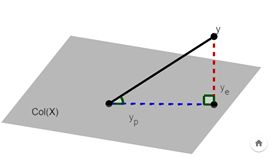
找到一个 X X X的列的线性组合,使得这个线性组合最多的表达 y y y中的信息。 由上图可知, y = y p + y e y = y_p+y_e y=yp+ye.当 y e y_e ye正交于 X X X列空间时,达到最小,此时, y p y_p yp与 y y y的夹角最小,即相关性最大。普通最小二乘法(OLS)的解如下
β ^ = ( X T X ) − 1 X T y \hat{\beta}=(X^TX)^{-1}X^Ty β^=(XTX)−1XTy
典型相关分析
典型相关分析是从两组数据 X X X和 Y Y Y中,找到两个相应的组合,使得两者相关性最大。其目标如下
a r g m a x w , c [ ( X w ) T ( Y c ) ] 2 ∣ ∣ ( X w ) ∣ ∣ 2 ∣ ∣ ( Y c ) ∣ ∣ 2 ⇔ a r g m a x w , c c o s ( X w , Y c ) 2 (2) arg \ \underset{w,c}{max} \frac{[(Xw)^T(Yc)]^2}{||(Xw)||^2||(Yc)||^2} \Leftrightarrow arg \ \underset{w,c}{max} \ cos(Xw,Yc)^2 \tag{2} arg w,cmax∣∣(Xw)∣∣2∣∣(Yc)∣∣2[(Xw)T(Yc)]2⇔arg w,cmax cos(Xw,Yc)2(2)
G c c a = [ ( X w ) T ( Y c ) ] 2 ∣ ∣ ( X w ) ∣ ∣ 2 ∣ ∣ ( Y c ) ∣ ∣ 2 ∈ [ 0 , 1 ] G_{cca} = \frac{[(Xw)^T(Yc)]^2}{||(Xw)||^2||(Yc)||^2} \ \in [0,1] Gcca=∣∣(Xw)∣∣2∣∣(Yc)∣∣2[(Xw)T(Yc)]2 ∈[0,1]
在单响应变量的情况下,则有 X w Xw Xw和 y y y的相关性最大,则可以得到
w ∝ ( X T X ) − 1 X T y w \propto (X^TX)^{-1}X^Ty w∝(XTX)−1XTy
主成分分析
PCA的思想是找到数据 X X X中代表最大方差方向的权值,通过减秩消除矩阵中的无关信息

这个方向的确定很容易,即 X T X X^TX XTX的最大特征向量
w ^ = a r g m a x w ^ w T X T X w = a r g m a x w ^ w T X T X w [ ρ ( X T X ) ] 2 s . t . ∣ ∣ w T w ∣ ∣ = 1 (3) \hat{w} = arg \ \underset{\hat{w}}{max} \ w^TX^TXw =arg \ \underset{\hat{w}}{max} \tfrac{w^TX^TXw}{[\rho(X^TX)]^2} \tag{3}\\ s.t. \ ||w^T w||=1 w^=arg w^max wTXTXw=arg w^max[ρ(XTX)]2wTXTXws.t. ∣∣wTw∣∣=1(3)
令 G p c r = w T X T X w [ p ( X T X ) ] 2 G_{pcr} = \tfrac{w^TX^TXw}{[p(X^TX)]^2} Gpcr=[p(XTX)]2wTXTXw, G p c r ∈ [ 0 , 1 ] G_{pcr} \in [0,1] Gpcr∈[0,1]
对比OLS和PCA可以发现,前者的目标是使得 G c c a G_{cca} Gcca最大化,后者是使 G p c r G_{pcr} Gpcr最大化。在实际应用中,两个目标往往难以同时达到最大。
第一种解释
P L S 可 以 看 作 是 C C A 和 P C A 的 一 个 折 中 。 \color{red}{PLS可以看作是CCA和PCA的一个折中。} PLS可以看作是CCA和PCA的一个折中。
PLS是一种数据减秩的方法,跟PCA类似,是用原数据的部分数据(成分)代替原始数据。构造成分的方法和CCA,PCA不同之处在于,PLS是两者的一个平衡点,由下面的目标式可以清楚得看到。
w ^ = a r g m a x w ^ ( y T X w ) 2 = a r g m a x w ^ ( ( y T X w ) 2 y T y w T X T X w ) ( ( w T X T X w ) [ ρ ( X T X ) ] 2 ) ( y t y ) = a r g m a x w ^ G c c a G p c r s . t . ∣ ∣ w T w ∣ ∣ = 1 (4) \hat{w} = arg \ \underset{\hat{w}}{max} \ (y^TXw)^2 =arg \ \underset{\hat{w}}{max} (\tfrac{ (y^TXw)^2}{y^Tyw^TX^TXw})(\tfrac{ (w^TX^TXw)}{[\rho(X^TX)]^2} )(y^ty) =arg \ \underset{\hat{w}}{max} \ G_{cca}G_{pcr} \tag{4}\\ \\s.t. \ ||w^T w||=1 w^=arg w^max (yTXw)2=arg w^max(yTywTXTXw(yTXw)2)([ρ(XTX)]2(wTXTXw))(yty)=arg w^max GccaGpcrs.t. ∣∣wTw∣∣=1(4)
更直观一些看下图,假设 ∣ ∣ w ∣ ∣ = 1 ||w||=1 ∣∣w∣∣=1,对于所有的可能的点 X w Xw Xw,构成了如下的的超椭圆空间。CCA,PCR,PLS在成分或者说得分向量的构造方式上存在以下的几何关系。
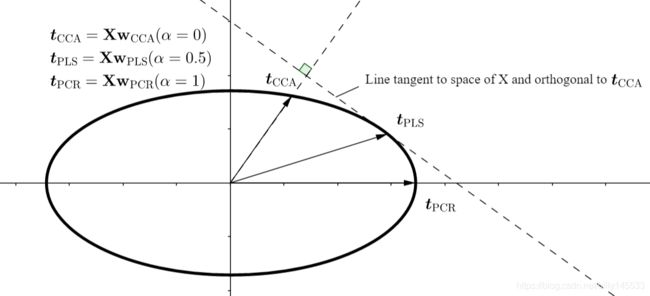
具体可以看参考文献部分
第二种解释
P L S 是 一 种 共 轭 梯 度 法 \color{green}{PLS是一种共轭梯度法} PLS是一种共轭梯度法
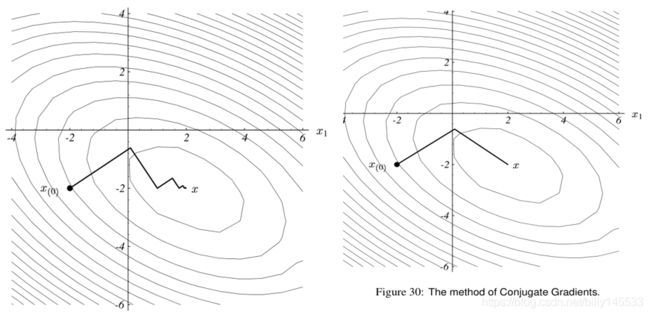
上图中,左边是最速下降法的优化路径,右图是共轭梯度下降法的优化路径。可见,共轭梯度法的效率要远高于最速下降法的速率。直观得看,最速下降法的缺点在走回头路,导致收敛速度缓慢,共轭梯度法的特点保证了其不走回头路,所以,收敛的速度是有保障的。所谓共轭,就是权值方向满足
w i T X T X w j = 0 , i ≠ j (5) w_i^TX^TXw_j=0,i \neq j \tag{5} wiTXTXwj=0,i=j(5)
这个的证明可以看前面的文章。无论是NIPALS(基于残差),SIMPLS(基于载荷矩阵正交投影)这一点都是可以满足的。
从几何的角度来看,构造共轭正交的权值,是为了保证得分向量 t = X w t=Xw t=Xw的正交性,因为得分矩阵 T T T最终代替X, 响应变量 y y y最终通过将自身投影到 T T T的空间中,获得 y y y和 T T T的回归关系。如下图所示, t t t是两两正交的,新增的 t i t_i ti不影响原来 y y y在其他 t j , j < i t_j,jtj,j<i上的投影, y y y因此一定是收敛的。

第三种解释
P L S 是 一 种 基 于 K r y l o v 空 间 降 维 打 击 的 方 法 。 \color{blue}{PLS是一种基于Krylov空间降维打击的方法。} PLS是一种基于Krylov空间降维打击的方法。
尽管Krylov空间和共轭梯度法是密不可分的,这里还是单独从这个角度谈谈。
Krylov subspaces 子空间的形式如下
K q = s p a n ( s , S s , S 2 , … , S q − 1 s ) (6) K_q = span(s,Ss,S^2,\dots,S^{q-1}s) \tag{6} Kq=span(s,Ss,S2,…,Sq−1s)(6)
KryLov空间常用于求解大型矩阵的逆
A x = b ⇒ x = A − 1 b A − 1 b ≈ β 0 b + β 1 A b + β 2 A 2 b + ⋯ + β r A r b = ∑ i = 0 r β i A i b A i b c a n b e o b t a i n e d b y J a c o b i a n F r e e N e w t o n K r y l o v A ( ∑ i = 0 r β i A i b ) = b ⇒ A − 1 b (7) Ax = b \Rightarrow x = A^{-1}b\\ A^{-1}b \approx \beta_0b+\beta_1Ab+\beta_2A^2b+\dots+\beta_rA^rb=\sum_{i=0}^{r}\beta_iA^ib \tag{7}\\ A^ib\ can\ be\ obtained\ by \ Jacobian\ Free\ Newton\ Krylov\\ A(\sum_{i=0}^{r}\beta_iA^ib) = b\Rightarrow A^{-1}b Ax=b⇒x=A−1bA−1b≈β0b+β1Ab+β2A2b+⋯+βrArb=i=0∑rβiAibAib can be obtained by Jacobian Free Newton KrylovA(i=0∑rβiAib)=b⇒A−1b(7)
和PLS的关系
L e t s = X T y , S = X T X f o r a l l w i ∗ , i ∈ ( 1 , r ) s p a n s p a c e K r K r = s p a n ( s , S s , S 2 s , … , S r − 1 s ) t i = X w i ∗ y ^ = X β ^ = λ 1 t 1 + ⋯ + λ r t r ∗ ⇒ β ^ P L S = λ 1 w 1 ∗ + ⋯ + λ r w r ∗ = ∑ i = 0 r − 1 β i S i s (8) Let \ s= X^Ty ,S = X^TX \\ for\ all \ w_i^*,i \in (1,r)\ span\ space\ K_r\\ K_r = span(s,Ss,S^2s,\dots,S^{r-1}s) \\ t_i = Xw_i^*\\ \\\hat{y}=X \hat{\beta} =\lambda_1t_1+\dots+\lambda_rt_r^* \Rightarrow\\\tag{8} \hat{\beta}_{PLS} = \lambda_1w^*_1+\dots+\lambda_rw_r^* =\sum_{i=0}^{r-1}\beta_iS^is Let s=XTy,S=XTXfor all wi∗,i∈(1,r) span space KrKr=span(s,Ss,S2s,…,Sr−1s)ti=Xwi∗y^=Xβ^=λ1t1+⋯+λrtr∗⇒β^PLS=λ1w1∗+⋯+λrwr∗=i=0∑r−1βiSis(8)
只要 r r r足够大, β ^ P L S → β ^ O L S \hat{\beta}_{PLS} \rightarrow \hat{\beta}_{OLS} β^PLS→β^OLS
第四种解释
最 大 化 信 噪 比 方 向 \color{#fbbc05}{最大化信噪比方向} 最大化信噪比方向
Maximinze Signal-To-Noise Ratio(SNR)体现了PLS在权值w上的选取意义
PLS的解是是有偏估量,本质上是以无偏估量 β O L S \beta_{OLS} βOLS解作为信号,以最大化信噪比的方向去提取 β O L S \beta_{OLS} βOLS中的信息,构造近似的解。
按照有偏估量的计算,可以得到如下方程
a r g m a x w q ∣ w T β ^ O L S ∣ σ w T ( X T X ) − 1 w ⇔ a r g m a x w q c o s ( w , β ^ O L S ) 2 w T ( X T X ) w , s . t . w q ⊥ ( w 1 , w 2 , … , w q − 1 ) (10) arg \ \underset{w_q }{max} \ \frac{|w^T\hat{\beta}_{OLS}|}{\sigma\sqrt{w^T(X^TX)^{-1}w}}\Leftrightarrow arg \ \underset{w_q }{max} \ cos(w,\hat{\beta}_{OLS})^2w^T(X^TX)w ,\tag{10}\\ \ s.t. \ w_q \perp (w_1,w_2,\dots,w_{q-1}) arg wqmax σwT(XTX)−1w∣wTβ^OLS∣⇔arg wqmax cos(w,β^OLS)2wT(XTX)w, s.t. wq⊥(w1,w2,…,wq−1)(10)
看上面左边的公式,分子部分代表了相关性,即信息最大,分母部分代表了噪声的估计量。两者结合在一起就是信噪比,这和PLS的目标是一致的。
对上式重写,可以转换为如下的形式
a r g m a x w q ∣ w q T β ^ O L S ∣ , s . t . w q ⊥ ( w 1 , w 2 , … , w q − 1 ) , w q T S − 1 w q = 1 arg \ \underset{w_q }{max} \ |w_q^T\hat{\beta}_{OLS}| , s.t. \ w_q \perp (w_1,w_2,\dots,w_{q-1}), \ w_q^TS^{-1}w_q=1 arg wqmax ∣wqTβ^OLS∣,s.t. wq⊥(w1,w2,…,wq−1), wqTS−1wq=1
λ q w q = − s − ∑ i = 1 q − 1 λ i ∗ S ∗ w i ⇒ β ^ P L S = λ 1 w 1 + ⋯ + λ r w r \lambda_qw_q = -s - \sum_{i=1 }^{q-1}\lambda_i*S*w_i \Rightarrow \hat{\beta}_{PLS} = \lambda_1w_1+\dots+\lambda_rw_r λqwq=−s−i=1∑q−1λi∗S∗wi⇒β^PLS=λ1w1+⋯+λrwr
总结
偏最小二乘当然还有许多其他的解释,这里不再一一介绍。一直以来,偏最小二乘法总是偏向于直觉,而缺乏坚实的理论而受到诟病,特别是统计学界。另外,目前的文献资料显示,偏最小二乘法的解绝并非统计学意义上的最优解,这一点已有诸多文献讨论并且做出相关证明。但由于其在小样本,高维共线的领域里出色效果,在化学计量,经济计量等受到广泛的应用。这里主要是将自己对偏最小二乘法的理解总结一下,以后大概不会再写普通的偏最小二乘法,更多地是讨论一下改进的偏最小二乘法,如稀疏,鲁棒等版本的偏最小二乘模型。
参考文献
Optimizing a vector of shrinkage factors for continuum regression