纹理特征描述及matlab实现
纹理特征描述图像或图像区域所对应景物的表面性质,是图像中计算出来的一个值,它对区域变化的特征进行量化。纹理分析是通过一定的图像处理技术抽取纹理特征,从而获得纹理的定量或定性描述的处理过程。
灰度差分统计法
纹理区域的灰度直方图作为纹理特征,利用图像直方图提取诸均值、方差、能量及熵等特征来描述纹理。设(x,y)为图像中的一点,该点和它只有微小距离的点(x+▲x,y+▲y)的灰度差值为:g▲(x,y) = g(x,y) - g(x+▲x,y+▲y),
其中,g▲称为灰度差分。设灰度差分值得所有可能取值共m级,令点(x,y)在整个画面上移动,统计出g▲取各个数值得次数,由此可以做出g▲得直方图。由直方图可以得到g▲取值概率p(k)的,当取较小插值k的频率p(k)较大时,反映了纹理交粗糙,直方图平坦时,说明纹理较细致。
相关纹理特征:
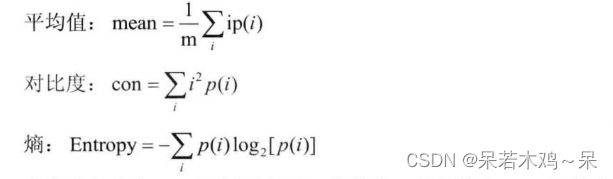
p(k)较平坦时,熵较大,能量较小,p(k)越分布在原点附近,则均值越小。
计算灰度差分法统计特征:
>> I = imread('E:\persional\matlab\images\house.tif');
>> A = double(I);
>> [m,n] = size(A);
>> B = A;
>> C = zeros(m,n);%新建全零矩阵
>> for i=1:m-1
for j=1:n-1
B(i,j) = A(i+1,j+1);
C(i,j) = abs(round(A(i,j)-B(i,j)));
end
end
>> h = imhist(mat2gray(C))/(m*n);%归一化灰度直方图
>> mean=0;con=0;ent=0;%均值,对比度和熵初始值为0
>> for i=1:256
mean = mean+(i*h(i))/256;
con = con+i*i*h(i);
if(h(i)>0)
ent = ent-h(i)*log2(h(i));
end
end
>> subplot(121),imshow(I),title('原图');
>> subplot(122),imshow(C),title('灰度差分');
>> mean
mean =
0.0382
>> con
con =
327.4435
>> ent
ent =
3.6956
自相关函数法
纹理常用来描述粗糙性,小数值的纹理测度表示细纹理,大数值测度表示粗纹理,通常采用自相关函数作为纹理检测。设图像为f(x,y),自相关函数的定义为:

一般粗纹理区对给定偏离(ε,η)的相关性要比细纹理高,因而纹理粗造形应与自相关函数的扩展成正比。
定义自定义函数:
function [epsilon,eta,C] = zxcor(f,D,m,n)
for epsilon=1:D
for eta=1:D
temp = 0;
fp = 0;
for x=1:m
for y=1:n
if(x+epsilon-1)>m | (y+eta-1)>n
f1 = 0;
else
f1 = f(x,y)*f(x+epsilon-1,y+eta-1);
end
temp=f1+temp;
fp = f(x,y)*f(x,y)+fp;
end
end
f2(epsilon,eta)=temp;
f3(epsilon,eta)=fp;
C(epsilon,eta)=f2(epsilon,eta)/f3(epsilon,eta);
end
end
epsilon=0:(D-1);%ε方向取值范围
eta=0:(D-1);%η方向取值范围
调用zxcor()函数:
>> I = imread('E:\persional\matlab\images\0.jpg');
>> J = imread("E:\persional\matlab\images\2.jpg");
>> subplot(121),imshow(I),title('图一');
>> subplot(122),imshow(J),title('图二');
>> f1 = rgb2gray(I);
>> f2 = rgb2gray(J);
>> f1 = double(f1);
>> f2 = double(f2);
>> [m1,n1] = size(f1);
>> [m2,n2] = size(f2);
>> D=20;%偏移量
>> [epsilon1,eta1,C1] = zxcor(f1,D,m1,n1);
>> [epsilon2,eta2,C2] = zxcor(f2,D,m2,n2);
>> subplot(121),mesh(epsilon1,eta1,C1);
>> xlabel('epsilon');ylabel('eta');
>> subplot(122),mesh(epsilon2,eta2,C2);
>> xlabel('epsilon');ylabel('eta');


随着ε和η的增大,可见图一变化快,其表面纹理比较粗糙,图二趋近于平稳,可以说其纹理光滑,表面粗糙度越大,曲线变化快,粗造度越小,曲线变化慢。
灰度共生矩阵
由于纹理是由灰度分布在空间位置上反复出现而形成的,因而在图像空间中相隔某距离的像素之间会存在一定的灰度关系,即图像中灰度的空间特征性。灰度共生矩阵就是一种通过研究灰度空间相关特性来描述纹理的常用方法。
灰度直方图是对图像上单个像素具有某个灰度进行统计的结果,而灰度共生矩阵是对图像上保持某距离的两像素分别具有某灰度的状况进行统计得到的。一幅图像的灰度共生矩阵能反映出图像灰度关于方向、相邻间隔和变化幅度的综合信息,它是分析图象的局部模式和它们排列规则的基础。
设f(x,y)为一幅二维数字图像,S为目标区域R中具有特定空间连续的像素对集合,则满足一定空间关系的灰度共生矩阵P为:
![]()
等号右边的分子具有某种空间关系、灰度值分别为g1和g2的像素对的个数,分母为像素对的总个数(#代表数量)。这样得到的P是归一化的,取不同的距离和角度则可能得到不同的灰度共生矩阵,求解过程过选定距离不变,去不同的角度,比如0°、45°、90°和135°的灰度共生矩阵。
如果图像是具有相似灰度值的像素块构成,则灰度共生矩阵的对角元素会有比较大的值;如果图像像素值在局部有变化,那么偏离对角线的元素会有比较大的值。
能量:
灰度共生矩阵元素值的平方和,反应图像灰度分布均匀程度和纹理粗细程度。如果灰度共生矩阵所有值相等,则能量越小;反之,如果一些值大而其他值小,则能量值大。当共生矩阵中元素集中分布时,此时能量值大,能量值大表示一种均一和规则变换=化的纹理模式。
![]()
对比度:
反应图像的清晰度和纹理沟纹深浅的程度,纹理沟纹越深,对比度大,视觉效果越清晰,反之对比度越小,视觉效果越模糊。灰度差即对比度大的像素对越多,这个值就大。灰度共生矩阵中远离对角线的元素值越大,对比度越大。

相关:
度量空间灰度矩阵元素在行列上的相似程度,因此,相关值大小反应了图像中局部灰度相关性。当矩阵元素值均匀相等时,相关值大;如果矩阵元素值相差很大,则相关值小。如果图像中有水平方向纹理,则水平方向矩阵的相关值大于其余矩阵的相关值。

熵:
图像具有的信息量的度量,纹理信息也是属于图像的信息,是一个随机性的度量,当共生矩阵中所有元素有最大的随机性、空间共生矩阵中所有的值几乎相等时,熵越大。它表示了图像中纹理的非均匀程度或复杂程度。

均匀度:
反映纹理的粗糙程度,粗纹理的均匀度较大,细纹理的均匀度较小。

共生矩阵函数graycomatrix()
‘GrayLimits’:两个元素的向量,表示图像中的灰度映射范围,如果设为[ ],灰度共生矩阵将使用图像I的最大值和最小值;
‘NumLevels’:将图像中的灰度归一范围,决定灰度共生矩阵的大小;
‘Offset’:为一个P×2的整数矩阵;
D:当前像素与邻居的距离,0°:[0 D]、45°:[-D D]、90°:[-D 0]和135°:[-D -D]。
>> I = imread('E:\persional\matlab\images\house.tif');
>> glcm = graycomatrix(I,'Offset',[0 2]);
>> glcm
结果显示原图的灰度共生矩阵对角线元素的值较大,表示图像中灰度值接近的像素块多

纹理特征统计值函数garycoprops():
stats = graycoprops(glcm,{‘contrast’,‘correlation’,‘energy’,‘homogeneity’}),返回值为灰度共生矩阵的静态属性;
glcm:灰度共生矩阵;
‘Contrast’:对比度,返回整幅图像中像素和它相邻像素之间的亮度反差,取值范围[0 ~ (glcm的行数-1)2];
‘Correlation’:相关性,图像中像素与其相邻像素是如何相关的度量值,取值范围为[-1,1];
‘Energy’:能量,像素的平方和,取值范围[0,1];
‘Homogemeity’:同质性,glcm中元素分布到对角线的紧密程度,取值范围[0,1],对角矩阵同质性为1。
遥感图像基于共生矩阵的纹理特征统计:
>> I = imread('map1.tif');
>> HSV = rgb2hsv(I);
>> Hgray = rgb2gray(HSV);
>> glcms1 = graycomatrix(Hgray,'numlevels',64,'offset',[0 1;-1 1;-1 0;-1 -1]);%纹理特征统计值(对比度、相关性、熵、平稳度二阶矩)
>> stars = graycoprops(glcms1,{'contrast','correlation','energy','homogeneity'});
>> ga1 = glcms1(:,:,1);%0°
>> ga2 = glcms1(:,:,2);%45°
>> ga3 = glcms1(:,:,3);%90°
>> ga4 = glcms1(:,:,4);%145°
>> energya1 = 0;energya2 = 0;energya3=0;energya4=0;
>> for i=1:64
for j=1:64
energya1 = energya1+sum(ga1(i,j)^2);
energya2 = energya2+sum(ga2(i,j)^2);
energya3 = energya3+sum(ga3(i,j)^2);
energya4 = energya4+sum(ga4(i,j)^2);
j=j+1;
end
i=i+1;
end
>> s1=0;s2=0;s3=0;s4=0;s5=0;%对比度
>>> for m=1:4
s1 = stars.Contrast(1,m)+s1;
end
>> for m=1:4
s2 = stars.Correlation(1,m)+s2;%相关性
end
>> for m=1:4
s3 = stars.Energy(1,m)+s3;%熵
end
>> for m=1:4
s4 = stars.Homogeneity(1,m)+s4;%平稳度
end
>> s5 = 0.000001*(energya1+energya2+energya3+energya4);%二阶矩


由图可得山脉对比度远高于城市和台风;山脉与城市的相关性接近,台风的相关性为负值;台风的熵值与城市接近大于山脉;山脉和城镇的对比度和平稳度参数有一定的差距,可以用来区分山脉和海洋。
