多智能体强化学习-MAAC

引入注意力机制的actor-critic强化学习

论文链接：https://arxiv.org/pdf/1810.02912.pdf

代码链接：https://github.com/shariqiqbal2810/MAAC

摘要

本文主要思想是学习一个具有注意力机制的集中式critic。（CTDE方法中，训练时拥有上帝视角，提高学习效率，通过从所有智能体那里获得的消息进行集中学习critic，执行时各自独立决策actor），在训练期间的每个时间点动态的选择要关注的智能体，从而在具有复杂交互的多智能体环境中提高性能。（有点像MADDPG和COMA的结合体）(off-policy)

方法

将多智能体任务建模为POMDP框架$\mathcal{G}(S,A,O,P,R,\gamma )$，智能体部分可观测，每个智能体学习一个策略${\pi }_i:O_i\to P(A_i)$，${\pi }_i$将每个智能体的观测值映射到其对应的一系列动作的分布。智能体的目标是学习一个使其期望折扣回报最大的策略：$$J_i({\pi }_i)=E_{a_1\sim {\pi }_1,...,a_N\sim {\pi }_N,s\sim T}[\sum _{t=0}{\gamma }^t{r}_{it}(s_t,a_{1t},...,a_{Nt})]$$

策略梯度评估：

$${\nabla }_{\theta }J({\pi }_{\theta })={\nabla }_{\theta }log({\pi }_{\theta }(a_t|s_t))\sum _{t^{\prime }=t}{\gamma }^{t^{\prime }-t}r{t}^{\prime }(s_{t^{\prime }},a_{t^{\prime }})$$

actor- critic

${\gamma }^{t^{\prime }-t}r{t}^{\prime }(s_{t^{\prime }},a_{t^{\prime }})$会带来高方差，actor-critic的方法旨在利用except-return的函数估计来缓解这个问题，例如学习一个函数来估计给定状态，动作的excepted discounted returns，通过off-policy的TD，最小化回归损失：
$$L_Q(\varphi )=E_{(s,a,r,s^{\prime })\sim D}[(Q_{\varphi }(s,a)-y{)}^2]y=r(s,a)+\gamma E{a}^{\prime }\sim \pi (s^{\prime })[(Q_{(\varphi )}(s^{\prime },a^{\prime }))]$$

soft actor-critic

为了鼓励探索，避免收敛到非最优的确定性策略，提出了最大熵强化学习方法- soft value function，在策略梯度中加入熵项：
$${\nabla }_{\theta }J({\pi }_{\theta })=E_{s\sim D,a\sim \pi }[{\nabla }_{\theta }log({\pi }_{\theta }(a|s))(-\alpha log({\pi }_{\theta }(a|s))+Q_{\varphi }(s,a)-b(s))]$$
相应的，值函数的时序差分TD的损失函数也修改为一个新的目标：
$$y=r(s,a)+\gamma E_{a^{\prime }\sim \pi (s^{\prime })}[(Q_{\varphi )}(s^{\prime },a^{\prime })-\alpha log({\pi }_{\theta }(a^{\prime }|s^{\prime }))]$$

MAAC

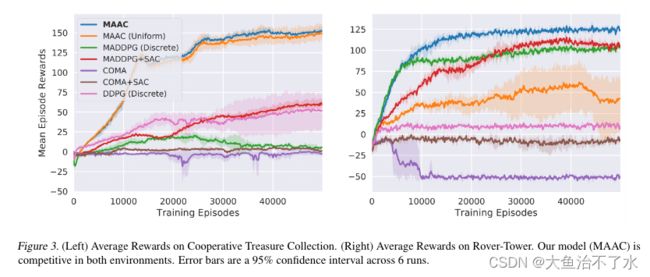
主要思想：利用attention机制从其他智能体的观测-动作对中选取重要的信息来构造每个智能体的critic的输入，解决扩展性问题，帮助智能体有选择性的筛选出重要的环境信息，忽略不重要的信息。
attention：每个智能体向其他智能体查询相关的O和A，并将这些信息合并到值函数的估计中。$Q_i^{\varphi }(o,a)$是由智能体i的O和A，以及其他智能体的信息贡献：
$$Q_i^{\varphi }(o,a)=f_i(g_i(o_i,a_i),x_i)$$
$o_i,a_i$表示所有智能体的观测集合和动作集合。$f_i$$g_i$是两层的MLP，$g_i$用于对智能体的观测-动作对进行embedding编码.
$x_i$是其他智能体贡献的加权和
$$x_i=\sum _{i\ne j}{\alpha }_{ij}{v}_j=\sum _{ij}{\alpha }_{j}h(V{g}_j(o_j,a_j))$$
attention机制：${\alpha }_{ij}$是智能体i对智能体j的注意力权重，$v_j$是智能体j的观测-动作对的embedding，过程如下：首先用$g_j$进行embedding编码，然后利用共享矩阵V 完成线性转换，最后进行非线性操作 h.（例如ReLU）。
${\alpha }_{ij}$通过比较智能体i和智能体j的embedding向量的相似性（$e_i,e_j$），得到：
${\alpha }_{ij}\propto exp(e_j^T{W}_k^T{W}_q{e}_i)$
其中，$W_q$将$e_i$映射为query，$W_k^T$将$e_j$映射为key

MAAC中将来自不同attention head的贡献作为单个向量进行串联作为critic的输入，每一个head可以专注于不同智能体的混合权重。
所有的extracting 选择符，键，值（$W_k,W_q,V$）的权重在所有的智能体之间共享，形成一个共同的嵌入空间。这种参数共享能够在异构智能体的情况下学到共同的embedding空间。
MAAC的思想就是将其他智能体的观测-动作对先进行embedding操作然后利用注意力权重加权相加然后再与自身智能体的观测-动作对连接起来作为critic的输入，注意力权重度量了两个智能体embedding的相似程度。直观上来看，这样做能够让智能体更多地关注与自己相似的智能体，理论上来说对信息的利用率应该更高，另外通过将所有智能体的观测-动作对合并成一个单维度向量，也解决了扩展性问题。
critic更新：（和COMA类似）
由于参数共享，所有的critic一起更新以最小化联合回归损失函数：
$$L_Q(\psi )=\sum _{i=1}^N{E}_{(o,a,r,o^{\prime })\sim D}[(Q_i^{\psi }(o,a)-y_i{)}^2]$$
$$y_i=r_i+\gamma E_{a^{\prime }\sim {\pi }_{\theta (o^{\prime })}}[Q_i^{\psi }(o^{\prime },a^{\prime })-\alpha log({\pi }_{{\theta }_i}(a_i^{\prime }|o_i^{\prime }))]$$
每个智能体策略（policy）的更新：（和COMA类似）
$${\nabla }_{{\theta }_i}J({\pi }_{\theta })=E_{s\sim D,a\sim \pi }[{\nabla }_{{\theta }_i}log({\pi }_{{\theta }_i}(a_i|o_i))(-\alpha log({\pi }_{{\theta }_i}(a_i|o_i))+Q_i^{\varphi }(o,a)-b(o,a_i))]$$
$b(o,a_i)$用反事实基线计算优势函数，和COMA类似。
在MADDPG中，其他智能体的动作是直接从经验池回放中采样，这样可能会导致过采样，在MAAC中，所有智能体的动作都从当前策略中采样，保证智能体体能够在当前策略上进行协同。

实验部分

实验环境

1.测试算法的可扩展性，合作环境
2.测试算法处理与奖励相关信息的能力，例如足球比赛（信用分配）